Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение некоторых типовых задач, рассматриваемых в аудитории ⇐ ПредыдущаяСтр 4 из 4
19.3.1. Решить уравнение Решение. Делим обе части уравнения на
Ответ: 19.3.2. Решить уравнение Решение. Приведём уравнение к виду: Делим обе части уравнения на выражение Переменные разделены. Интегрируем обе части уравнения: При делении выражения на 19.3.3. Решить уравнение Решение. Обозначим Подставляя
Возвращаясь к старым переменным, получим:
19.3.4. Решить уравнение Решение. Разделим обе части уравнения на 19.3.5. Решить уравнение Решение. С учетом начального условия получим
19.4. Задачи для самостоятельного решения 19.4.1. Ответы. 19.4.1. 19.4.3. 19.4.6. 19.5. Однородные уравнения. Решения типовых задач Однородные уравнения могут быть записаны в виде 19.5.1. Решить уравнение Решение. Это однородное уравнение. Пусть
Ответ: 19.5.2. Решить уравнение Решение.
Разделяя переменные и затем интегрируя, имеем:
Переходя к старым переменным, получим окончательный ответ: 19.5.3. Решить уравнение Решение.
Уравнение вида 19.5.4. Решить уравнение Решение. Отсюда 19.5.5. Решить уравнение Решение.
19.6. Задачи для самостоятельного решения ДИСТАНЦИОННОЕ ОБУЧЕНИЕ 19.6.1. 19.6.3. Ответы. 19.6.1. 19.6.3.
|
|||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 74; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.178.157 (0.01 с.) |
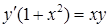 .
. .
.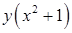 , получим
, получим  , интегрируем
, интегрируем 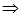
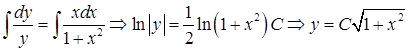 - общее решение данного уравнения. При делении выражения на
- общее решение данного уравнения. При делении выражения на 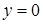 , но оно входит в общее решение при
, но оно входит в общее решение при  .
. .
.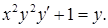
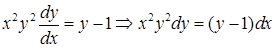 .
. , получим
, получим 
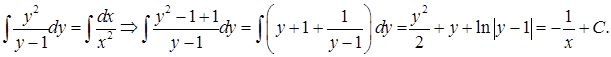
 могли быть потеряны решения
могли быть потеряны решения 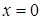 и
и 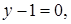 т. е.
т. е. 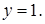 Очевидно,
Очевидно, 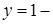 решение уравнения, а
решение уравнения, а  нет. Ответ:
нет. Ответ: 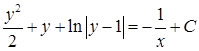 ;
; 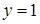 .
.
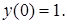
 , тогда
, тогда 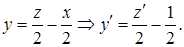
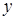 и
и  в данное уравнение, получим:
в данное уравнение, получим: 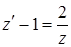 , откуда следует
, откуда следует 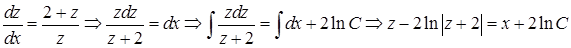 .
.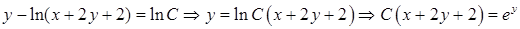 — общий интеграл уравнения. Учитывая начальное условие, получим частный интеграл:
— общий интеграл уравнения. Учитывая начальное условие, получим частный интеграл:  . Ответ:
. Ответ:  .
.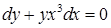 .
. . При делении на
. При делении на 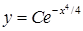 .
. 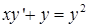 ;
; 
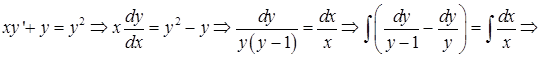

 Ответ:
Ответ: 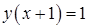 .
.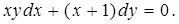 19.4.2.
19.4.2. 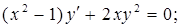
 19.4.3
19.4.3 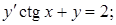
 19.4.4.
19.4.4. 
 19.4.5.
19.4.5.  19.4.6.
19.4.6. 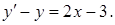 19.4.7.
19.4.7. 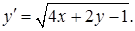
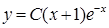 и
и  19.4.2.
19.4.2. 
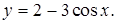 19.4.4.
19.4.4.  19.4.5.
19.4.5. 
 19.4.7.
19.4.7. 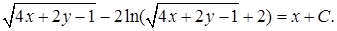
 а также в виде
а также в виде 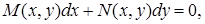 где
где 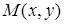 и
и  — однородные функции одной и той же степени. (Функция
— однородные функции одной и той же степени. (Функция  , если для всех
, если для всех  имеем
имеем 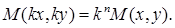 ) Чтобы решить однородное уравнение, можно сделать замену
) Чтобы решить однородное уравнение, можно сделать замену  после чего получается уравнение с разделяющимися переменными.
после чего получается уравнение с разделяющимися переменными.
 Тогда
Тогда 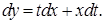 Подставляя в уравнение, получим
Подставляя в уравнение, получим 
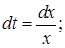
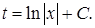 Возвращаясь к старому переменному
Возвращаясь к старому переменному 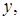 запишем
запишем  Кроме того, имеется решение
Кроме того, имеется решение 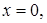 которое было потеряно при делении на
которое было потеряно при делении на 
 .
.
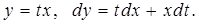 Подставляем в уравнение
Подставляем в уравнение  ; сокращая на
; сокращая на  , получим:
, получим: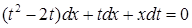
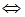
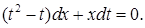


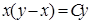 .
.
 Проведём замену
Проведём замену  и подставим ее в уравнение:
и подставим ее в уравнение: 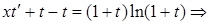
 . Разделяя переменные
. Разделяя переменные  и интегрируя, запишем
и интегрируя, запишем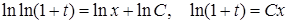 . Возвращаясь к старым переменным, получим ответ:
. Возвращаясь к старым переменным, получим ответ: 
 приводится к однородному с помощью переноса начала координат в точку
приводится к однородному с помощью переноса начала координат в точку  пересечения прямых
пересечения прямых  и
и  заменой
заменой 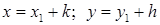 . Если же эти прямые не пересекаются, то
. Если же эти прямые не пересекаются, то 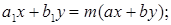 следовательно, уравнение имеет вид
следовательно, уравнение имеет вид  и приводится к уравнению с разделяющимися переменными заменой
и приводится к уравнению с разделяющимися переменными заменой 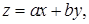 см. замечание в п. 19.2 и пример 19.3.3.
см. замечание в п. 19.2 и пример 19.3.3.
 . Это уравнение, приводящееся к однородному с помощью параллельного переноса осей координат:
. Это уравнение, приводящееся к однородному с помощью параллельного переноса осей координат: 
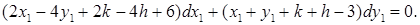 Решая систему линейных уравнений
Решая систему линейных уравнений  , найдём:
, найдём:  .
. 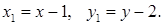
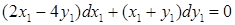 — однородное уравнение. Проводим известные уже замены
— однородное уравнение. Проводим известные уже замены 


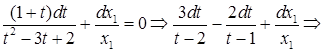
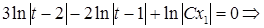


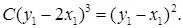 Возвращаясь к старым переменным, получим окончательный ответ
Возвращаясь к старым переменным, получим окончательный ответ 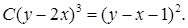
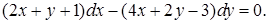
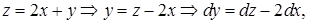 подставим в уравнение:
подставим в уравнение: 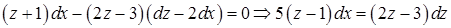 . Разделяя переменные
. Разделяя переменные 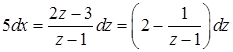 и интегрируя, после возвращения к старым переменным, получим ответ
и интегрируя, после возвращения к старым переменным, получим ответ 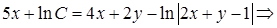
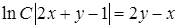
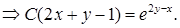
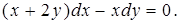 19.6.2.
19.6.2. 
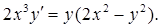 19.6.4.
19.6.4. 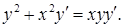 19.6.5.
19.6.5. 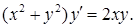 19.6.6.
19.6.6. 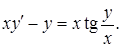
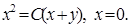 19.6.2.
19.6.2. 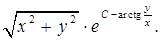
 19.6.4.
19.6.4.  19.6.5.
19.6.5. 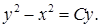 19.6.6.
19.6.6.