
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение некоторых типовых задач, рассматриваемых в аудиторииСодержание книги
Поиск на нашем сайте
16.3.1. Вычислить ротор векторного поля Решение. Здесь
Итак, 16.3.2. Найти по формуле Стокса циркуляцию векторного поля Решение. Выберем в качестве поверхности 16.3.3. Вычислить циркуляцию вектора Решение. Как видно из параметрического задания кривой, Теперь найдем ротор:
Вычислим теперь циркуляцию непосредственно, используя параметрическое задание контура:
16.3.4. Найти циркуляцию вектора
Решение. Контур состоит из двух дуг парабол и четверти окружности (рис. 16.2). Направление обхода контура, указанное в условии, соответствует выбору внешней нормали По формуле Стокса Вычислим ротор
Итак, циркуляция равна 16.3.5. Найти циркуляцию векторного поля Решение. Ротор этого поля найден в примере 16.3.1. В качестве поверхности, опирающейся на контур, выберем участок плоскости
16.4. Задачи для самостоятельного решения ДИСТАНЦИОННОЕ ОБУЧЕНИЕ 16.4.1. Найти 16.4.2. Решить задачу 14.5.5 б) с помощью формулы Стокса. 16.4.3. Найти циркуляцию векторного поля 16.4.4. Вычислить циркуляцию вектора 16.4.5. Найти циркуляцию векторного поля 16.4.6. Вычислить циркуляцию векторного поля
Ответы. 16.4.1. а) ЧАСТЬ Б) ДТСТАНЦИОННОЕ ОБУЧЕНИЕ СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ
|
||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |

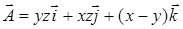 .
.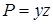 ,
, 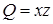 и
и 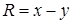 . Компоненты ротора равны
. Компоненты ротора равны 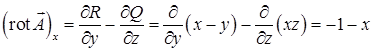 ,
, 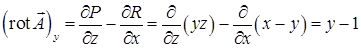 ,
,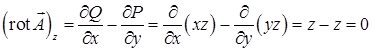 .
.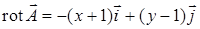 .
.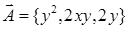 по окружности
по окружности 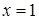 ,
, 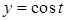 ,
, 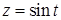 , ориентированной против часовой стрелки при взгляде на нее из начала координат.
, ориентированной против часовой стрелки при взгляде на нее из начала координат.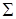 , ограниченной данной окружностью
, ограниченной данной окружностью 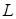 , круг
, круг 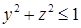 при
при 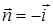 . Найдем ротор векторного поля:
. Найдем ротор векторного поля: 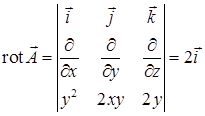 , тогда
, тогда 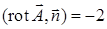 . По формуле Стокса
. По формуле Стокса 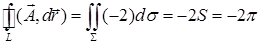 , где
, где 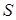 – площадь круга
– площадь круга 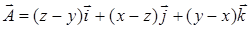 вдоль контура
вдоль контура  в направлении, соответствующем возрастанию параметра
в направлении, соответствующем возрастанию параметра 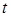 . Задачу решить по формуле Стокса и прямым вычислением.
. Задачу решить по формуле Стокса и прямым вычислением.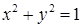 и плоскости
и плоскости 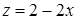 . В качестве поверхности
. В качестве поверхности 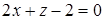 с положительной аппликатой, т. е.
с положительной аппликатой, т. е. 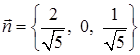 .
.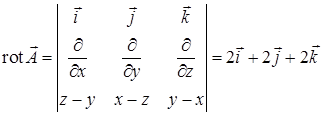 . Скалярное произведение
. Скалярное произведение 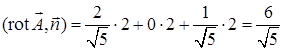 . По формуле Стокса циркуляция равна
. По формуле Стокса циркуляция равна 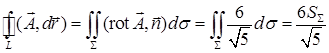 . Проекцией эллипса на плоскость
. Проекцией эллипса на плоскость 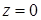 является окружность
является окружность 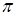 . Косинус угла между плоскостями
. Косинус угла между плоскостями 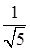 , тогда по формуле площади проекции
, тогда по формуле площади проекции 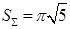
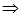
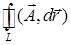
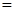
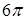 .
.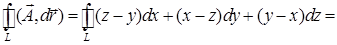
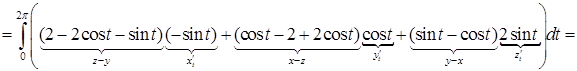
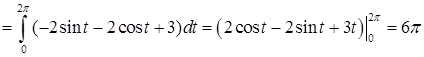 .
.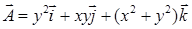 вдоль контура
вдоль контура 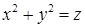 плоскостями
плоскостями 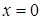 ,
, 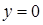 ,
, 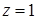 при
при 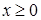 ,
, 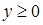 . Контур
. Контур 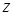 .
.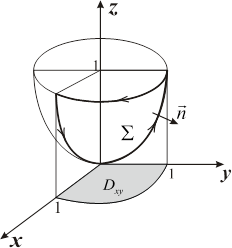
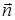 к параболоиду, т. е. нормали с отрицательной аппликатой. В качестве поверхности
к параболоиду, т. е. нормали с отрицательной аппликатой. В качестве поверхности 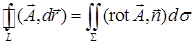
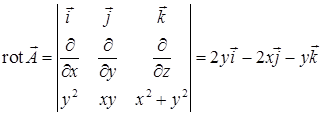 . Чтобы найти поток ротора, выберем метод проектирования на одну координатную плоскость, изложенный в п. 13.1, а именно, на плоскость
. Чтобы найти поток ротора, выберем метод проектирования на одну координатную плоскость, изложенный в п. 13.1, а именно, на плоскость 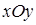 . Проекцией поверхности
. Проекцией поверхности 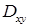 радиуса
радиуса 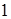 . Уравнение поверхности
. Уравнение поверхности 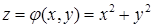 , компоненты ротора
, компоненты ротора 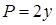 ,
, 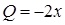 ,
, 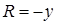 . Учтем, что, в отличие от п. 13.1, мы выбрали нормаль к
. Учтем, что, в отличие от п. 13.1, мы выбрали нормаль к 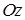 , поэтому
, поэтому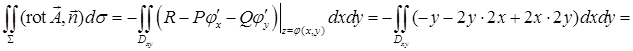
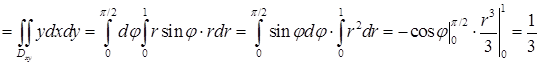 .
.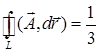 .
.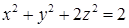 с плоскостью
с плоскостью 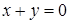 .
.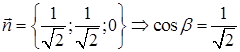 ,
, 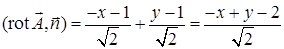 . На выбранной поверхности
. На выбранной поверхности 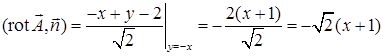 . Исключим из уравнений эллипсоида и плоскости
. Исключим из уравнений эллипсоида и плоскости 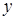 :
: 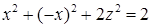 , или
, или 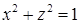 . Следовательно, проекция поверхности интегрирования
. Следовательно, проекция поверхности интегрирования 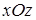 есть круг радиуса 1. По формуле Стокса получаем:
есть круг радиуса 1. По формуле Стокса получаем: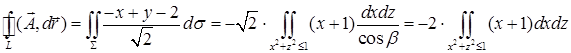 . Двойной интеграл вычислим в полярных координатах:
. Двойной интеграл вычислим в полярных координатах: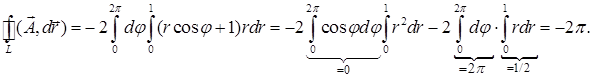
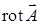 , если: а)
, если: а) 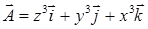 ; б)
; б) 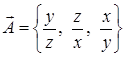 .
.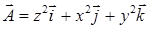 по сечению сферы
по сечению сферы 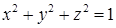 плоскостью
плоскостью 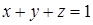 в положительном направлении обхода относительно вектора
в положительном направлении обхода относительно вектора 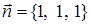 .
.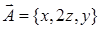 вдоль контура
вдоль контура 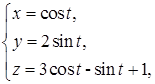 пробегаемого в направлении возрастания параметра
пробегаемого в направлении возрастания параметра 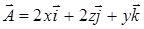 по ломаной
по ломаной 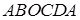 , где
, где 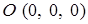 ,
, 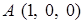 ,
, 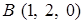 ,
, 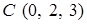 ,
, 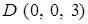 — вершины прямоугольного параллелепипеда. При вычислении по теореме Стокса в качестве поверхности, опирающейся на контур, выберите часть поверхности этого параллелепипеда.
— вершины прямоугольного параллелепипеда. При вычислении по теореме Стокса в качестве поверхности, опирающейся на контур, выберите часть поверхности этого параллелепипеда.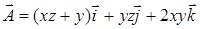 по контуру, вырезанному из двуполостного гиперболоида
по контуру, вырезанному из двуполостного гиперболоида 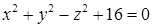 плоскостями
плоскостями 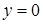 и
и 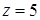 при
при 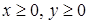 .
. ; б)
; б) 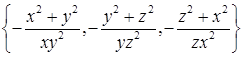 . 16.4.3.
. 16.4.3.  . 16.4.4.
. 16.4.4. 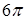 . 16.4.5.
. 16.4.5. 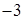 . 16.4.6.
. 16.4.6. 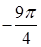 .
.


