Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Механическая работа, кинетическая энергия, консервативные и неконсервативные силыСодержание книги
Поиск на нашем сайте
Содержание
Введение 3 Глава 1. Механическая работа, кинетическая энергия, консервативные и неконсервативные силы 5 1.1 Механическая работа 5 1.2 Кинетическая энергия 7 1.3 Консервативные и неконсервативные силы 11 Глава 2. Потенциальная энергия в поле силы тяжести, потенциальная энергия упругого деформированного тела 15 2.1 Потенциальная энергия в поле силы тяжести 15 2.2 Потенциальная энергия упруго деформированного тела 18 Глава 3. Полная энергия системы, закон сохранения энергии в механике 22 3.1 Полная энергия системы 22 3.2 Закон сохранения энергии в механике 26 Заключение 34 Список литературы 35 Введение
Энергия может переходить из одного вида в другой, может переходить от одного тела к другому, но общий запас механической энергии остаётся неизменным. Опыты и теоретические расчеты показывают, что при отсутствии сил трения и при воздействии только сил упругости и тяготения суммарная потенциальная и кинетическая энергия тела или системы тел остается во всех случаях постоянной. В этом и заключается закон сохранения механической энергии. Закон сохранения энергии является фундаментальным законом природы. В физике различают несколько видов энергии, которые также являются базовыми видами энергии, способными переходить один в другой. Это обусловило актуальность нашего исследования. Целью работы является описание существующих в механике типов работы, а также подробное описание закона сохранения энергии в механике. Для того, чтобы достичь поставленной цели необходимо решить ряд задач: - проанализировать научные публикации по заданной теме исследования; - подробно рассмотреть и описать виды энергии в механике, дать характеристику закону сохранения энергии; - сделать обобщающие выводы по итогам проделанной работы. Актуальность исследования для деятельности Войск национальной гвардии обуславливается тем, что создание различных инженерно-технических комплексов, исследование вооружения, военной и специальной техники невозможно без учета различного типа энергии и учета закона сохранения энергии, т.к. еще на стадии разработки есть возможность просчитать потенциальное распределение энергии. Поскольку закон сохранения энергии является фундаментальным законом природы, то его актуальность не вызывает сомнений. Законы сохранения не зависят ни от траекторий частиц, ни от характера действующих сил. Поэтому они позволяют получить ряд весьма общих и существенных заключений о свойствах различных механических процессов без их детального рассмотрения с помощью уравнений движения. Если, например, выясняется, что некий анализируемый процесс противоречит законам сохранения, то можно утверждать: этот процесс невозможен, и бессмысленно пытаться его осуществить. Научно-практическая значимость работы обусловлена тем, что в ней дается описание одного из важнейших явлений, существующих в нашем мире – энергии, а также ее сохранения. Поэтому исследование может быть использовано для изучения основных видов энергии, популяризации физических явлений, с которыми человек сталкивается каждый день в своей жизни. Работа состоит из введения, трех глав, заключения и списка литературы.
Глава 1. Механическая работа, кинетическая энергия, консервативные и неконсервативные силы Механическая работа
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Если действующая на тело сила вызывает его перемещение s, то действие этой силы характеризуется величиной, называемой механической работой. Механическая работа А — скалярная величина, равная произведению модуля силы F, действующей на тело, и модуля перемещения s, совершаемого телом в направлении действия этой силы.
Если направления перемещения тела и приложенный силы не совпадают, то работу можно вычислить как произведение модулей силы и перемещения, умноженному на косинус угла α между векторами силы
Поскольку работа является скалярной величиной, она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы. Работа силы Если проекция
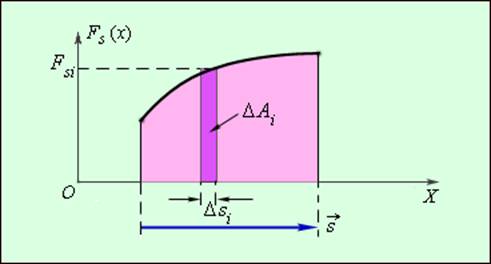
Это сумма в пределе (Δsi → 0) переходит в интеграл. Графически работа определяется по площади криволинейной фигуры под графиком Fs(x) (рисунок 1).
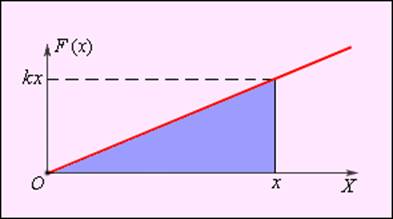
Рисунок 1. Графическое определение работы. ΔAi = FsiΔsi Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рисунок 2).
Рисунок 2. По площади треугольника на рисунке 2 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил. Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
Кинетическая энергия
Энергия — это способность тела работать, а также сила, которая выполняет работу. Она может быть представлена в виде различных переходных форм: тепловой; механической; химической; электрической; ядерной. В физике самая важная форма называется механической энергией. Это сумма и определение потенциальной и кинетической энергии, формула которой: E = Ek + Wp. Кинетическая энергия — это энергия, создаваемая движущимся телом. На греческом языке кинетика означает «движение», в то время как энергия означает «работа». Другими словами, кинетическая энергия — это работа, которую тело выполняет, когда оно движется. Мы можем воспользоваться кинетической энергией многих природных явлений. Например, движение воды в реке превращается в электричество благодаря электростанциям. Энергия ветра — это кинетическая энергия воздуха. Когда мы прибиваем гвоздь молотком, мы используем кинетическую энергию молотка при его перемещении. Её определяют как силу, необходимую для ускорения тела определённой массы от покоя до максимальной указанной скорости. Как только достигается ускорение, тело сохраняет энергию, если скорость не изменяется. Чтобы тело вернулось в состояние покоя, необходима отрицательная работа той же величины. Единица измерения кинетической энергии — джоуль. Обычно она обозначается буквой E c или E k. Расчёт мощности измеряется по-разному. Кинетическая энергия в физике измеряется в джоулях, сокращенно буквой J. Для расчета кинетической энергии тел используется уравнение:
Это означает, что кинетическая энергия Ec равна массе тела m, умноженной на квадрат скорости v, делённые на 2. Можно сделать вывод, что чем больше масса, тем больше энергия, и что энергия пропорциональна скорости, умноженной на себя. Кинетическая энергия не является вектором. Это означает, что если вы бросаете шар со скоростью 5 м/с, шар будет иметь одинаковую кинетическую энергию, независимо от того, бросаете ли вы его влево или вправо или вверх. Кинетическая энергия зависит от массы и скорости тела. Это означает, что чем больше или быстрее объект, тем больше энергии он производит. Примером вышесказанного может быть следующее: грузовик больше, чем автомобиль; Если оба едут с одинаковой скоростью и врезаются в стену, урон, нанесенный грузовиком, будет больше. В этом случае грузовик обладает большей кинетической энергией. Таким образом, кинетическая энергия зависит от квадрата скорости. Это означает, что когда скорость объекта удваивается, его кинетическая энергия увеличивается в четыре раза. Автомобиль, движущийся со скоростью 60 км/ч, имеет в четыре раза больше кинетической энергии, чем автомобиль, движущийся со скоростью 30 км/ч, и, следовательно, в четыре раза больший потенциал разрушения в случае аварии. Кинетическая энергия материальной точки равна:
где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной. Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:
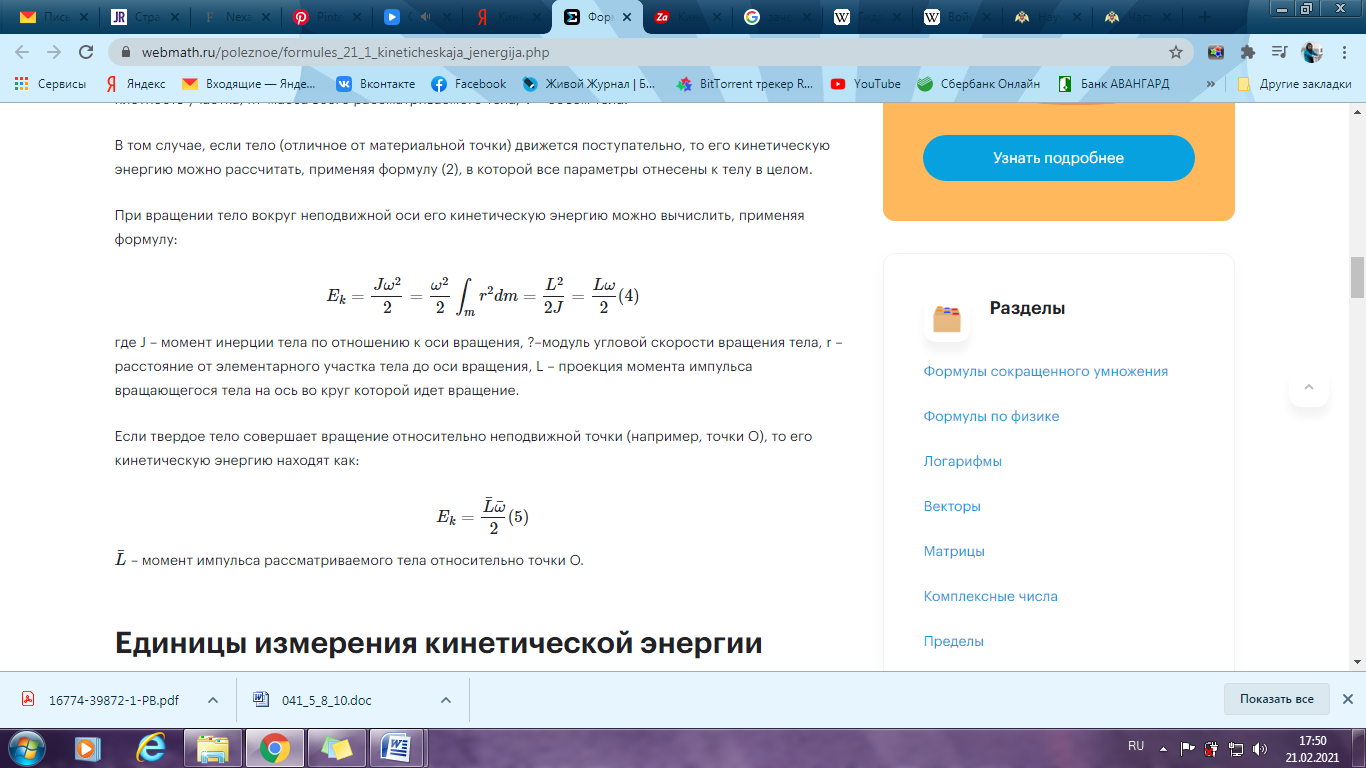
где dm – элементарный участок тела, который можно считать материальной точкой, dV – объем выделенного элементарного участка тела, v – скорость перемещения рассматриваемого элемента, ρρ - плотность участка, m–масса всего рассматриваемого тела, V – объем тела. В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом. При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:
где J – момент инерции тела по отношению к оси вращения,?–модуль угловой скорости вращения тела, r – расстояние от элементарного участка тела до оси вращения, L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение. Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:
L – момент импульса рассматриваемого тела относительно точки О. Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит: [Ek]=Дж (джоуль), в системе СГС –[Ek]= эрг. При этом: 1 дж= 107 эрг. Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой, кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения системы со скоростью центра масс (vc) и кинетической энергии (E'k) системы при ее относительном движении к поступательному перемещению системы отсчета. При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:
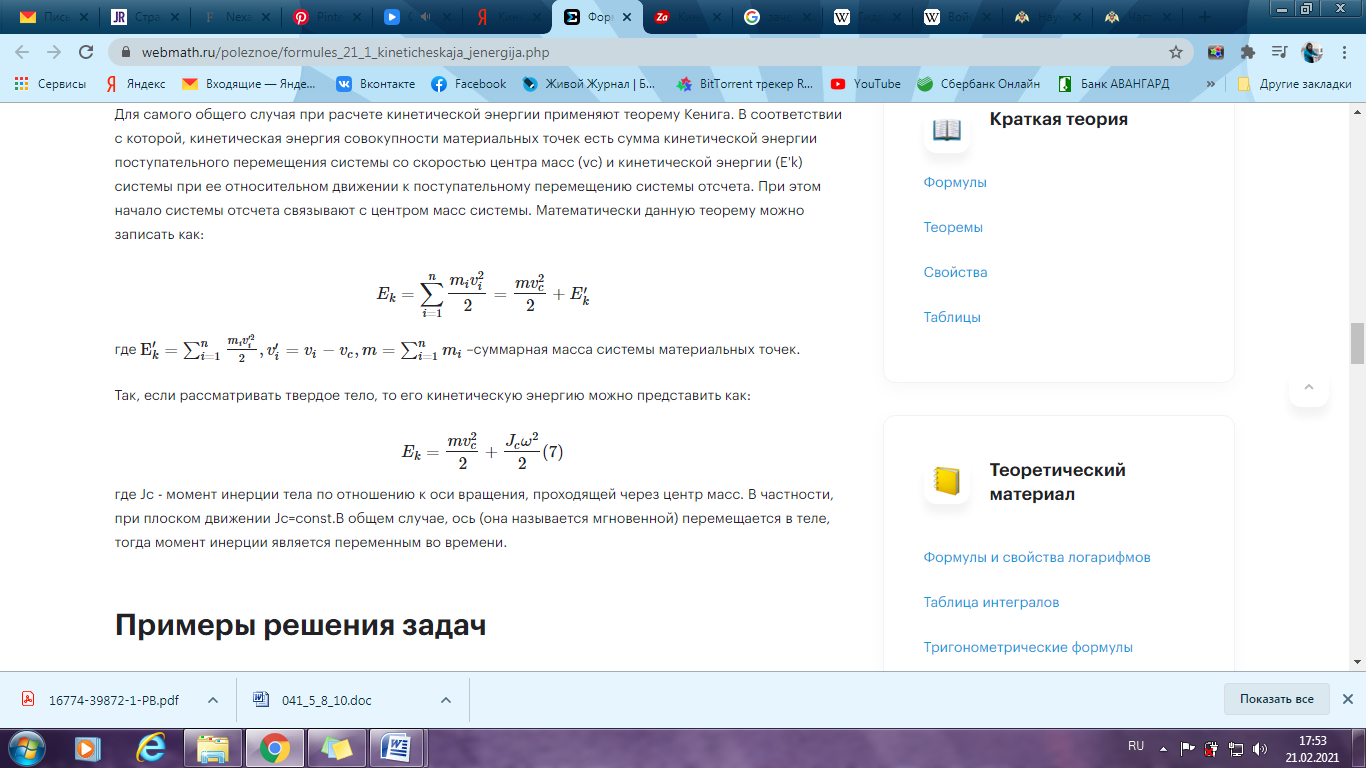
Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:
где Jc - момент инерции тела по отношению к оси вращения, проходящей через центр масс. В частности, при плоском движении Jc=const.В общем случае, ось (она называется мгновенной) перемещается в теле, тогда момент инерции является переменным во времени.
Полная энергия системы
Энергия тела — физическая величина, которая показывает работу, совершаемую рассматриваемым телом в течение любого, в том числе неограниченного периода времени. Полной энергией системы тел называется сумма потенциальной и кинетической энергий данной системы тел. Формула полной энергии системы тел: W = E + U здесь E – кинетическая, U – потенциальная энергия системы тел. Тела внутри изолированной системы тел взаимодействуют. При этом полная энергия системы не меняется, хотя энергия внутри системы может переходить из одного вида в другой. Это закон сохранения энергии: Полная энергия изолированной системы тел остаётся постоянной. При движении тел происходят превращения одного вида энергии в другой. Чтоб изменить полную энергию системы тел, на неё надо подействовать внешними силами. Работа этих внешних сил и будет равна изменению полной энергии системы. Но и система тел может совершить работу над внешними телами. Полная энергия системы определяет величину такой возможной работы. Объект, который совершает положительную работу, расходует частично энергию. В случае, когда положительную работу совершают над телом, его энергия возрастает. Если рассматривается отрицательная работа, то эффект будет противоположным. Таким образом, энергия выражается через физическую величину, характеризующую способность тела или системы взаимодействующих объектов совершать работу. Единицей измерения энергии в СИ является Джоуль (Дж). Кинетическая энергия - это энергия тел, находящихся в движении. В качестве движущихся тел рассматриваются не только перемещающиеся тела, но и объекты, которые вращаются. Кинетическая энергия возрастает по мере увеличения массы тела и скорости, с которой оно движется, то есть перемещается, либо вращается в пространстве. Кинетическая энергия определяется телом, по отношению к которому проводят измерения скорости рассматриваемого объекта. Потенциальная энергия — энергия тел или их частей, которые взаимодействуют друг с другом. Потенциальная энергия тел отличается в зависимости от силы, которая на них воздействует: · сила тяжести; · сила упругости; · архимедова сила. Любая потенциальная энергия определяется силой взаимодействия и расстоянием между взаимодействующими телами или их частями. Для расчета потенциальной энергии выбирают какой-то условный нулевой уровень. В качестве примера потенциальной энергии можно рассмотреть энергию, которой будет обладать груз, поднятый на определенную высоту над поверхностью Земли, или сжатая пружина. Энергия может трансформироваться из одного вида в другой. Так кинетическая энергия объекта может преобразоваться в его потенциальную энергию, и наоборот. Механическая энергия тела — это сумма его кинетической и потенциальной энергий. Механическая энергия любого тела определяется несколькими факторами: 1. Объект, относительно которого выполняют измерение скорости рассматриваемого тела. 2. Условные нулевые уровни, присущие всем разновидностям имеющихся у тела потенциальных энергий. Данная величина является одной из основных характеристик тела. С помощью механической энергии определяют способность тела или системы объектов совершать работу по причине изменений скорости тела, либо взаимного положения тел, находящихся во взаимодействии. Закон сохранения и превращения энергии: энергия не может возникать ниоткуда, либо исчезать бесследно. Можно лишь наблюдать переход одного вида энергии в другой, либо от одного тела к другому. Закон сохранения механической энергии: когда тела системы испытывают на себе воздействие силы тяжести или силы упругости, сумма кинетической и потенциальной энергии не будет изменяться, таким образом, механическая энергия сохраняется. Изменение механической энергии системы тел определяется, как сумма работы внешних по отношению к системе тел и работы внутренних сил трения и сопротивления. Формула для расчета имеет следующий вид: ΔW=Aвнешн+АдиссипΔ В случае замкнутой системы тел ее полная механическая энергия будет изменена только в том случае, когда совершается работа внутренних диссипативных сил системы таких, как сила трения: Aвнешн = 0, то ΔW = Адиссип Когда рассматривают консервативную систему тел, то есть при отсутствии сил трения и сопротивления, полная механическая энергия системы тел изменяется при работе внешних, относительно системы тел, сил: Атр=0Атр=0 ΔW=AвнешнΔW=Aвнешн Полная механическая энергия тела определяется суммой его кинетической и потенциальной энергии. Определение полной механической энергии справедливо в случае действия закона сохранения энергии, и ее постоянном значении. В ситуации, когда тело движется без влияния внешних сил, включая отсутствие взаимодействия с другими телами, силы трения и силы сопротивления, полная механическая энергия тела не меняется со временем. С помощью формулы это утверждение можно записать следующим образом: Епот+Екин=const В реальном мире нельзя смоделировать таких идеальных ситуаций, в условиях которых объект полностью сохраняет свою энергию. Причиной этому является постоянное взаимодействие тела с другими телами, к примеру с молекулами воздуха или сопротивлением воздуха. В случаях, когда сила сопротивления минимальна, и поступательное или другое движение наблюдают в относительно короткое время, подобную систему можно принять за теоретически идеальную. Как правило, закон сохранения полной механической энергии справедлив для тела, совершающего свободное падение, при вертикальном подбрасывании объекта или в случае колебательного движения тела такого, как маятник. В начале пути тело обладает кинетической энергией, которая будет равна его потенциальной энергии в верхней точке траектории движения. Полная энергия системы является суммой внешней и внутренней энергии системы. Внешняя энергия системы состоит из кинетической и потенциальной энергий системы как целого. Внутренняя энергия системы – это энергия системы, зависящая только от ее внутреннего состояния и не включающая в себя виды энергии системы как целого. Внутреннюю энергию системы U можно, в частности, найти, измеряя работу системы в адиабатном процессе (то есть при Q = 0): Аад D= — U, что определяет U с точностью до некоторой аддитивной постоянной U0: U = U + U0 Первое начало термодинамики утверждает, что U является функцией состояния системы, то есть каждое состояние термодинамической системы характеризуется определённым значением U, независимо от того, каким путём система приведена в данное состояние (в то время как значения Q и А зависят от процесса, приведшего к изменению состояния системы). При исследовании термодинамических свойств физической системы первое начало термодинамики обычно применяется совместно со вторым началом термодинамики. В современной термодинамике второе начало термодинамики изолированных систем формулируется единым и самым общим образом как закон возрастания особой функции состояния системы, которую Клаузиус назвал энтропией (S). dФизический смысл энтропии состоит в том, что в случае, когда материальная система находится в полном термодинамическом равновесии, элементарные частицы, из которых состоит эта система, находятся в неуправляемом состоянии и совершают различные случайные хаотические движения. В принципе можно определить общее число этих всевозможных состояний. Параметр, который характеризует общее число этих состояний, и есть энтропия.
Заключение
Энергия – это общая мера различных процессов и видов взаимодействия. Механической энергией называют физическую величину, характеризующую способность тела или системы тел совершить работу. Энергия тела или системы тел определяется максимальной работой, которую они способны совершить в данных условиях. К механической энергии относят два вида энергии – кинетическую и потенциальную. Законы сохранения энергии образуют тот фундамент, на котором основывается преемственность физических теорий. Действительно, рассматривая эволюцию важнейших физических концепций в области механики, электродинамики, теории теплоты, современных физических теорий, можно убедиться в том, что в этих теориях неизменно присутствуют либо одни и те же классические законы сохранения (энергии, импульса и др.), либо наряду с ними появляются новые законы, образуя тот стержень, вокруг которого и идет истолкование экспериментальных фактов. «Общность законов сохранения в старых и новых теориях является еще одной формой внутренней взаимосвязи последних». Само понятие энергии было выработано именно в поисках связей между различными формами движения материи. Переход энергии из одной формы в другую означает, что энергия в данной ее форме исчезает, превращается в энергию в иной форме. Для количественной характеристики различных форм движения вводятся соответствующие им виды энергии: механическая, внутренняя (тепловая), электромагнитная, химическая, ядерная и т. д. Закон сохранения энергии — закон, управляющий всеми явлениями природы, исключений из него науке неизвестно.
Список литературы
1. Антошина, Л.Г., Павлов, С.В., Скипетрова, Л.А. Общая физика. Сборник задач / Л.Г. Антошина, С.В. Павлов, Л.А. Скипетрова. - М.: Инфра-М, 2008. - 336 с. 2. Блохинцев, Д.И. Основы квантовой механики / Д.И. Блохинцев. - СПб.: Лань, 2004. - 672 с. 3. Бутырский Г.А., Сауров Ю.А. Экспериментальные задачи по физике. – М.: Просвещение, 2001. – 157 с. 4. Вигнер Э. Инвариантость и законы сохранения энергии. – М.: Издательство «Эдиториал», 2002. – 357 с. 5. Гершензон Е.М., Малов Н.Н. Курс общей физики: Механика. – М.: Просвещение, 2007. – 127 с. 6. Дуков, В.М. История формулировки закона сохранения энергии / В.М. Дуков // Физика. - М.: Первое сентября. - 2002. - № 31/02. - С. 32-34. 7. Кубо, Р. Термодинамика / Р. Кубо. - М.: Наука, 2007. - 307 с. 8. Савельев И.В, Курс общей физики, том 1. Механика, колебания и волны, молекулярная физика. – М.: Издательство «Наука», 2007 – 352 с. 9. Сивухин, Д.В. Общий курс физики / Д.В. Сивухин. - М.: Физматлит, 2004. - 656 с. 10. Типлер, П.А., Ллуэллин, Р.А. Современная физика / П.А. Типлер, Р.А. Ллуэллин. - М.: Мир, 2007. - 496 с. 11. Яворский Б.М., Пинский А.А. Основы физики. – М.: Наука, 2002. – 102 с.
Содержание
Введение 3 Глава 1. Механическая работа, кинетическая энергия, консервативные и неконсервативные силы 5 1.1 Механическая работа 5 1.2 Кинетическая энергия 7 1.3 Консервативные и неконсервативные силы 11 Глава 2. Потенциальная энергия в поле силы тяжести, потенциальная энергия упругого деформированного тела 15 2.1 Потенциальная энергия в поле силы тяжести 15 2.2 Потенциальная энергия упруго деформированного тела 18 Глава 3. Полная энергия системы, закон сохранения энергии в механике 22 3.1 Полная энергия системы 22 3.2 Закон сохранения энергии в механике 26 Заключение 34 Список литературы 35 Введение
Энергия может переходить из одного вида в другой, может переходить от одного тела к другому, но общий запас механической энергии остаётся неизменным. Опыты и теоретические расчеты показывают, что при отсутствии сил трения и при воздействии только сил упругости и тяготения суммарная потенциальная и кинетическая энергия тела или системы тел остается во всех случаях постоянной. В этом и заключается закон сохранения механической энергии. Закон сохранения энергии является фундаментальным законом природы. В физике различают несколько видов энергии, которые также являются базовыми видами энергии, способными переходить один в другой. Это обусловило актуальность нашего исследования. Целью работы является описание существующих в механике типов работы, а также подробное описание закона сохранения энергии в механике. Для того, чтобы достичь поставленной цели необходимо решить ряд задач: - проанализировать научные публикации по заданной теме исследования; - подробно рассмотреть и описать виды энергии в механике, дать характеристику закону сохранения энергии; - сделать обобщающие выводы по итогам проделанной работы. Актуальность исследования для деятельности Войск национальной гвардии обуславливается тем, что создание различных инженерно-технических комплексов, исследование вооружения, военной и специальной техники невозможно без учета различного типа энергии и учета закона сохранения энергии, т.к. еще на стадии разработки есть возможность просчитать потенциальное распределение энергии. Поскольку закон сохранения энергии является фундаментальным законом природы, то его актуальность не вызывает сомнений. Законы сохранения не зависят ни от траекторий частиц, ни от характера действующих сил. Поэтому они позволяют получить ряд весьма общих и существенных заключений о свойствах различных механических процессов без их детального рассмотрения с помощью уравнений движения. Если, например, выясняется, что некий анализируемый процесс противоречит законам сохранения, то можно утверждать: этот процесс невозможен, и бессмысленно пытаться его осуществить. Научно-практическая значимость работы обусловлена тем, что в ней дается описание одного из важнейших явлений, существующих в нашем мире – энергии, а также ее сохранения. Поэтому исследование может быть использовано для изучения основных видов энергии, популяризации физических явлений, с которыми человек сталкивается каждый день в своей жизни. Работа состоит из введения, трех глав, заключения и списка литературы.
Глава 1. Механическая работа, кинетическая энергия, консервативные и неконсервативные силы Механическая работа
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Если действующая на тело сила вызывает его перемещение s, то действие этой силы характеризуется величиной, называемой механической работой. Механическая работа А — скалярная величина, равная произведению модуля силы F, действующей на тело, и модуля перемещения s, совершаемого телом в направлении действия этой силы.
Если направления перемещения тела и приложенный силы не совпадают, то работу можно вычислить как произведение модулей силы и перемещения, умноженному на косинус угла α между векторами силы
Поскольку работа является скалярной величиной, она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы. Работа силы Если проекция
Это сумма в пределе (Δsi → 0) переходит в интеграл. Графически работа определяется по площади криволинейной фигуры под графиком Fs(x) (рисунок 1).
Рисунок 1. Графическое определение работы. ΔAi = FsiΔsi Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рисунок 2).
Рисунок 2. По площади треугольника на рисунке 2 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил. Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
Кинетическая энергия
Энергия — это способность тела работать, а также сила, которая выполняет работу. Она может быть представлена в виде различных переходных форм: тепловой; механической; химической; электрической; ядерной. В физике самая важная форма называется механической энергией. Это сумма и определение потенциальной и кинетической энергии, формула которой: E = Ek + Wp. Кинетическая энергия — это энергия, создаваемая движущимся телом. На греческом языке кинетика означает «движение», в то время как энергия означает «работа». Другими словами, кинетическая энергия — это работа, которую тело выполняет, когда оно движется. Мы можем воспользоваться кинетической энергией многих природных явлений. Например, движение воды в реке превращается в электричество благодаря электростанциям. Энергия ветра — это кинетическая энергия воздуха. Когда мы прибиваем гвоздь молотком, мы используем кинетическую энергию молотка при его перемещении. Её определяют как силу, необходимую для ускорения тела определённой массы от покоя до максимальной указанной скорости. Как только достигается ускорение, тело сохраняет энергию, если скорость не изменяется. Чтобы тело вернулось в состояние покоя, необходима отрицательная работа той же величины. Единица измерения кинетической энергии — джоуль. Обычно она обозначается буквой E c или E k. Расчёт мощности измеряется по-разному. Кинетическая энергия в физике измеряется в джоулях, сокращенно буквой J. Для расчета кинетической энергии тел используется уравнение:
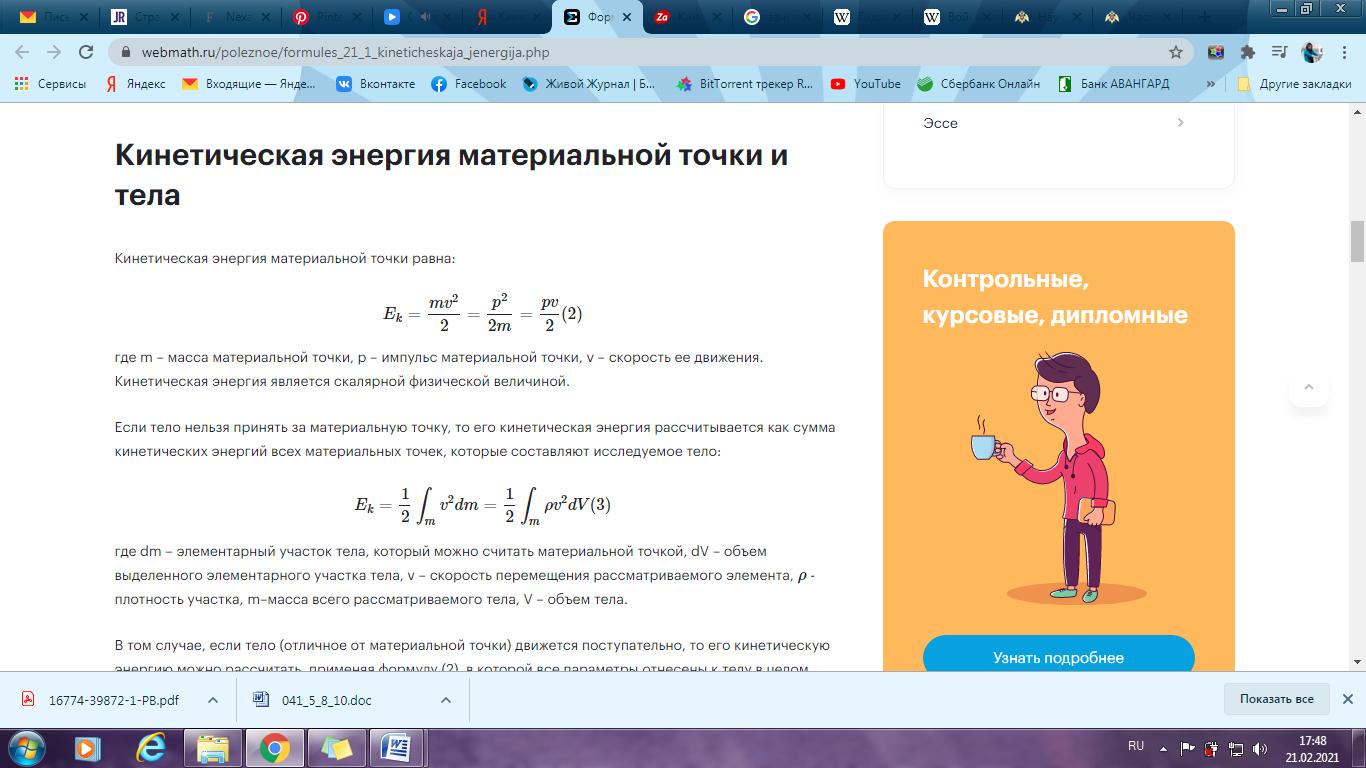
Это означает, что кинетическая энергия Ec равна массе тела m, умноженной на квадрат скорости v, делённые на 2. Можно сделать вывод, что чем больше масса, тем больше энергия, и что энергия пропорциональна скорости, умноженной на себя. Кинетическая энергия не является вектором. Это означает, что если вы бросаете шар со скоростью 5 м/с, шар будет иметь одинаковую кинетическую энергию, независимо от того, бросаете ли вы его влево или вправо или вверх. Кинетическая энергия зависит от массы и скорости тела. Это означает, что чем больше или быстрее объект, тем больше энергии он производит. Примером вышесказанного может быть следующее: грузовик больше, чем автомобиль; Если оба едут с одинаковой скоростью и врезаются в стену, урон, нанесенный грузовиком, будет больше. В этом случае грузовик обладает большей кинетической энергией. Таким образом, кинетическая энергия зависит от квадрата скорости. Это означает, что когда скорость объекта удваивается, его кинетическая энергия увеличивается в четыре раза. Автомобиль, движущийся со скоростью 60 км/ч, имеет в четыре раза больше кинетической энергии, чем автомобиль, движущийся со скоростью 30 км/ч, и, следовательно, в четыре раза больший потенциал разрушения в случае аварии. Кинетическая энергия материальной точки равна:
где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной. Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:
где dm – элементарный участок тела, который можно считать материальной точкой, dV – объем выделенного элементарного участка тела, v – скорость перемещения рассматриваемого элемента, ρρ - плотность участка, m–масса всего рассматриваемого тела, V – объем тела. В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом. При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:
где J – момент инерции тела по отношению к оси вращения,?–модуль угловой скорости вращения тела, r – расстояние от элементарного участка тела до оси вращения, L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение. Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:
L – момент импульса рассматриваемого тела относительно точки О. Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит: [Ek]=Дж (джоуль), в системе СГС –[Ek]= эрг. При этом: 1 дж= 107 эрг. Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой, кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения системы со скоростью центра масс (vc) и кинетической энергии (E'k) системы при ее относительном движении к поступательному перемещению системы отсчета. При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:
Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:
где Jc - момент инерции тела по отношению к оси вращения, проходящей через центр масс. В частности, при плоском движении Jc=const.В общем случае, ось (она называется мгновенной) перемещается в теле, тогда момент инерции является переменным во времени.
|
||||
|
Последнее изменение этой страницы: 2021-07-19; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.36.168 (0.018 с.) |

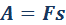
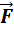 и перемещения
и перемещения 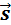 :
: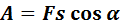
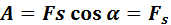
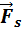 силы
силы  не остается постоянной, работу следует вычислять для малых перемещений Δsi и суммировать результаты:
не остается постоянной, работу следует вычислять для малых перемещений Δsi и суммировать результаты: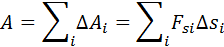
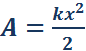
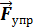 равна по модулю работе внешней силы
равна по модулю работе внешней силы 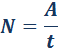
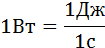
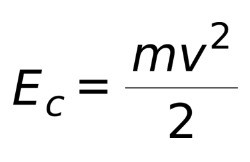
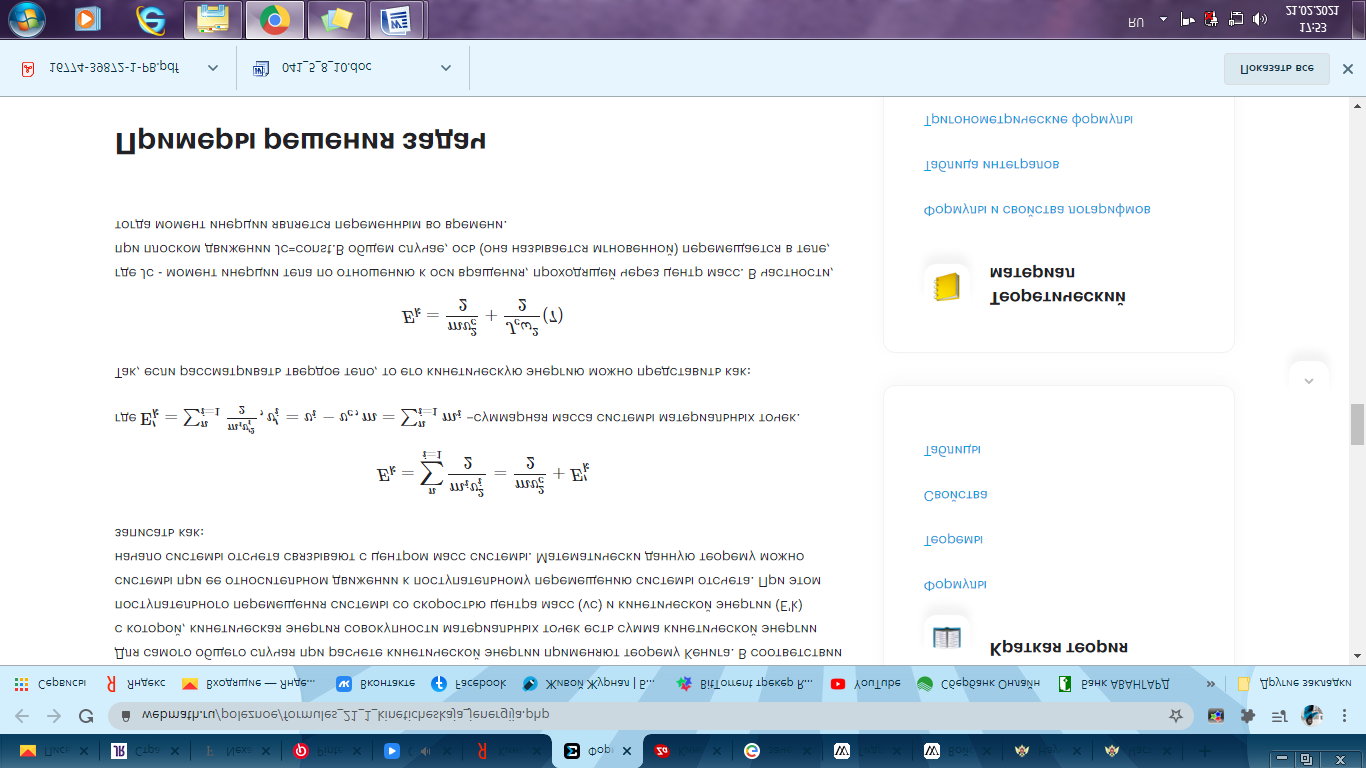 где - суммарная масса системы материальных точек.
где - суммарная масса системы материальных точек.