
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Турбулентные течения. Подходы к моделированию.Содержание книги
Поиск на нашем сайте
Тема 4. Турбулентные течения. Подходы к моделированию. Характеристики турбулентных потоков. Многообразие турбулентных потоков. Масштабы и подходы к моделированию турбулентных течений. Метод DNS, метод LES, методы RANSE. Характерные черты турбулентного течения.
Подавляющее большинство течений в инженерных приложениях турбулентные. Переход от ламинарного к турбулентному течению происходит при числах Re>2*103. При этих Re ламинарное течение становится неустойчивым.
Турбулентное течение принципиально отличается от ламинарного. Характерные особенности турбулентного течения: - Нестационарное, непериодическое движение, пространственно-временные флуктуации; в этом движении участвуют вихреподобные структуры (турбулентные вихри); - В турбулентном течении происходит постоянное порождение крупных структур (вихрей) которые перемещаются не только вместе с потоком, но и поперек потока; такое движение приводит к интенсификации процессов переноса массы импульса и энергии, т.к. обмен массой, импульсом и энергией между слоями жидкости осуществляется не только на молекулярном, но прежде всего, на макроскопическом уровне; - Параметры потока изменяются случайным образом; - В турбулентном течении происходит каскадный перенос энергии. Так основное стационарное течение неустойчиво, в нем образуются вихревые структуры, тем самым происходит отбор энергии от основного течения и передача его вихрям. Но вихри также являются неустойчивыми и распадаются на более мелкие структуры, передавая им свою энергию, те в свою очередь, распадаются на еще более мелкие и т.д. Процесс распада продолжается до образования самых мелких устойчивых вихрей, которые за счет трения переводят свою кинетическую энергию в тепло. Существует три масштаба вихрей: - энергосодержащий; - инерционный; - диссипативный.
Семейство k - e моделей турбулентности. К k-e моделей относят три модели турбулентности – стандартную, RNG и realizable. Это двухпараметрические модели, состоящие из транспортных уравнений для кинетической энергии турбулентности и скорости диссипации. Кажущаяся вязкость рассчитывается по найденным k и e. Стандартная модель была предложена Лаундером и Сполдингом в 1974 г. И с тех пор стала настоящей рабочей лошадью в инженерных расчетах. Устойчивость, экономичность и достаточная точность для многих приложений объясняют ее популярность. Она является полуэмпирической моделью. Затраты компьютерного времени. Модель Sk-e требует большего времени, чем однопараметрическая (SA), в силу большего числа уравнений. Realizable k-e потребляет ненамного больше времени чем Sk-e. RNG из-за присутствия дополнительных членов и функций в уравнениях, а также из-за большей нелинейности потребляет на 10-15% времени больше.
Стандартная k- e модель.
Этот набор констант используется по умолчанию. Он получен по результатам тестирования модели и сравнения с экспериментальными данными, полученными на воде и воздухе для фундаментальных турбулентных сдвиговых слоев, включая однородные сдвиговые слои и разрушающуюся изотропную турбулентность за решетками. Константы были подобраны так, чтобы обеспечивать удовлетворительные результаты для широкого класса течений.
RNG k- e модель. В отличие от Sk-e, RNG строго выводится с применением теории ренормализации групп. По форме она напоминает Sk-e, но включает следующие элементы: - Уравнение для скорости диссипации включает дополнительные члены, которые обеспечивают большую точность при расчете быстро деформирующихся течений; - Учет влияния вращения на параметры турбулентности, включенный в RNG, улучшает точность при расчетах вращающихся потоков; - Теория RNG обеспечивает получение аналитической формулы для числа Прандтля, тогда как Sk-e использует определенную пользователем величину. - Sk-e является высокорейнольдсовой моделью, а RNG включает аналитически выведенную формулу для эффективной вязкости, которая учитывает низкорейнольдсовые эффекты. Эффективное использование этой формулы, однако, зависит от выбора пристеночного алгоритма; Эти особенности делают RNG модель более точной и надежной по сравнению со Sk-e.
Модель эффективной вязкости получается на основе теории RNG и сводится к дифференциальному уравнению
Сn» 100. Это дифференциальное уравнение обеспечивает отслеживание зависимости от числа Рейнольдса для потоков с низким Re и пристеночных слоев. В пределе, при высоких числах Re
Характеристики турбулентности сильно зависят от закрутки осредненного течения. Для учета влияния закрутки применяется коррекция вида
Величины, обратные числам Прандтля рассчитываются следующим образом
a0 =1. Для больших Re (mt >>m) ak=ae»1,393. Наибольшие отличия между RNG и SKE проявляются из-за наличия члена Re в модели RNG. Благодаря ему при расчетах течений с малой и средней степенью деформации RNG сравнима с SKE, а в области сильно деформированных течений турбулентная вязкость снижается по сравнению с SKE. Набор констант этой модели
Реализуемая. Realizable k-e модель сравнительно недавно разработана и отличается от стандартной k-e по следующим двум пунктам: - Realizable k-e модель содержит новую формулировку для турбулентной вязкости; - Новое уравнение для скорости диссипации, e, которое получено из точного уравнения переноса среднеквадратичной завихренности; Термин реалистичная означает, что модель удовлетворяет некоторым ограничениям на напряжения Рейнольдса, вытекающие из физики турбулентных течений. Ни стандартная ни RNG этим ограничениям не удовлетворяют, следовательно, они не реализуемы. Чтобы понять смысл этого запишем уравнение для нормальных напряжений, полученное на основе гипотезы Буссинеска
Отсюда следует, что при достаточно больших сдвигах осредненного течения нормальные напряжения, которые по определению должны быть >0, могут стать отрицательными. Чтобы избежать этого, необходимо изменять константу Cm в зависимости от деформации среднего течения и от параметров турбулентности. На это указывают не только теория, но и экспериментальные результаты, согласно которым в инерционной области Cm = 0,09, а в однородном сдвиговом слое 0,05.
Непосредственные преимущества Realizable k-e модели заключаются в большей точности прогноза расширения как круглых, так и плоских струй. Она также обладает преимуществом при расчете течений с вращением, пограничных слоев с большим положительным градиентом давления, отрывом и рециркуляционными зонами.
Транспортные уравнения реализуемой модели
Турбулентная вязкость определяется как и в других k-e моделях
Но Cm рассчитывается в зависимости от деформации среднего течения и параметров турбулентности
Набор констант реализуемой модели
Генерация турбулентности во всех моделях k-e описана одинаково
Обе модели RNG и Realizable демонстрируют преимущество перед стандартной k-e моделью при расчете течений с большой кривизной линий тока, закруткой и вращением. Так как Realizable модель сравнительно новая, не вполне ясно, в чем она превосходит RNG. Однако некоторые результаты тестирования показали ее преимущество в определенном классе отрывных течений и потоков со сложными вторичными течениями. Серьезное ограничение Realizable k-e модели проявляется в нефизичном поведении турбулентной вязкости в тех случаях, когда расчетная область содержит и вращающуюся и неподвижную области.
Однопараметрические модели. Такие модели дают описание турбулентности с помощью одной переменной, для которой строится дифференциальное уравнение переноса. Другие характеристики турбулентности определяются через нее с помощью алгебраических соотношений. К однопараметрическим моделям относятся модели Колмогорова-Прандтля, Брэдшоу, Гуляева, Козлова, Секундова и др. Рассмотрим однопараметрическую модель Спалларта-Аллмареса. Эта модель конструировалась прежде всего для задач внешней аэродинамики и создана она была сравнительно недавно (конец 90-х). Уравнение для вихревой вязкости в этой модели записывается
Gn - генерация турбулентности; Y – разрушение турбулентности вблизи стенки из-за блокирующего действия стенки.
Коэффициенты и замыкающие функции записываются
Тензор Ωij = 0,5(∂ui/∂xj - ∂uj /∂xi) - тензор вращения, а d - расстояние от ближайшей стенки. Следует обратить внимание на то, что источниковые члены в уравнении для турбулентной вязкости зависят от расстояния до ближайшей стенки, а также от градиента турбулентной вязкости. При удалении от стенки модель пред- сказывает нераспадающуюся турбулентную вязкость в невозмущенном потоке. Опыт эксплуатации модели SA показал, что ее реальные возможности заметно шире, чем предполагалось при ее создании. Более того, после введения в нее по- правок на кривизну линий тока и вращение, границы ее применимости модели заметно расширились. В табл. 5.1 сведены результаты отклонений рассчитанных с помощью SA и измеренных коэффициентов трения в эталонных градиентных течениях. Таблица 5.1
Обнаружено, что предсказанный с помощью SA коэффициент трения так же близко соответствует измеренным величинам, как и алгебраическая модель Болдуина- Ломакса. Известно, что задача об обтекании обращенной назад ступеньки является весь- ма популярным тестом для анализа моделей турбулентности. На рис.19 показана схема одного из экспериментов, выполненных Драйвером и Сигмюллером (1985). Важным свойством рассматриваемого типа течения является то, что точка отрыва оказывается фиксированной в острой кромке ступенчатого канала. Гораздо сложнее прогнозировать течения с априори неизвестной точкой отрыва. На рис. 20 сравниваются расчетные и измеренные коэффициенты трения вдоль нижней стенки канала при нулевом отклонении верхней стенки от направления потока. Модель SA предсказывает длину отрывной зоны, измеренную в долях высоты ступеньки, равной 6.1. Она лишь на 2% отличается от экспериментальной величины 6.2H. При угле отклонения 6° модель предсказывает длину циркуляционной зоны в 8.6H, что на 6% отличается от измеренной величины 8.1H.
Таким образом, модель SA является удовлетворительной для многих инженерных приложений. В особенности она применима для расчета обтекания профилей и крыльев, для которых она была калибрована. В то же время, ее приемлемость для струйных задач менее убедительна. Показано (1997), что прогнозы коэффициента расширения осесимметричной затопленной струи по указанной модели вдвое отличаются от данных измерений. Резюмируя, следует отметить, что рассмотренный класс моделей с одним дифференциальным уравнением обладает большей приемлемостью к описанию турбулентных течений с учетом сжимаемости, переходных явлений, кривизны линий тока и отрыва потока. Однако объектами их приложения, как правило, являются простые конфигурации потоков с минимальным набором структурных элементов. Как и в случае алгебраических моделей, сильна привязка к калибровочным типам течений. Снять указанные ограничения можно, например, при определении масштаба турбулентности как зависимой переменной, т.е. в рамках двух- и многопараметрических моделей турбулентности.
Недостатки моделей на основе гипотезы Буссинеска: - Справедлива ли простая линейная связь между пульсациями и тензором кажущихся напряжений? Rij сильно зависит от параметров потока и предыстории; Rij изменяется со скоростью, не полностью зависящей от осредненного течения. Rij не строго связана с Sij для потоков: - с резко изменяющейся деформацией среднего течения; - с быстрым расширением, большой кривизной линий тока; - вращающихся потоков; - вторичных течений, индуцированных напряжениями. Пристеночные функции.
Почему необходимо использовать пристеночные функции? - Стенка генератор завихренности; - Точное моделирование пристеночных эффектов принципиально важно для многих инженерных приложений: -успешное прогнозирование силы сопротивления для внешних течений или потерь давления для внутренних течений; зависимость правильности прогноза от локальных параметров сдвигового течения вблизи стенки; Потери давления при обтекании плохообтекаемого тела зависят от протяженности зоны отрыва; Распределение температур определяется тепловыми потоками, которые полностью зависят от пристеночных эффектов;
На турбулентное течение значительное влияние оказывает присутствие стенки. В явном виде это проявляется через изменение профиля скорости вследствие условия прилипания, которое должно выполняться на стенке. Однако параметры турбулентности изменяются вблизи стенки нетривиальным образом. Вблизи стенки вязкость снижает тангенциальные флуктуации скорости, кинематическое блокирование уменьшает также и нормальные. С другой стороны, вблизи стенки турбулентность порождается вследствие большого градиента скорости (завихренность). Пристеночное моделирование значительно влияет на точность численного решения, так как стенка является главным источником завихренности среднего течения. И, наконец, в пристеночной области наблюдаются наибольшие изменения параметров потока. Отсюда и следует, что качественное решение в пристеночной области определяет успех всего расчета для ограниченных стенками потоков. k-e, RSM и LES модели разработаны для ядра потока (вдали от стенки). Следовательно, необходимо определится с тем, как эти модели сделать пригодными для пристеночных течений. Многочисленные эксперименты показали, что пристеночная область может быть поделена на три части. Внутренняя часть (примыкающая к стенке), называемая «вязким подслоем» представляет собой ламинарное течение, контролируемое вязкостью. Здесь силы вязкости намного превосходят силы инерции. Внешний слой, примыкающий к ядру потока, называется полностью турбулентным слоем. В этой области силы инерции намного превосходят вязкие силы, и турбулентный перенос является определяющим. Между ними располагается буферный или смешанный подслой, в котором силы инерции примерно равны силам вязкости и течение в равной мере контролируется как молекулярным переносом, так и турбулентным. На рис.5.1 представлены эти подобласти в полулогарифмических координатах.
Сдвиговое течение: течение с деформацией сдвига в профиле скорости: Пограничные слои на стенке, слои смешения. Существует два подхода к моделированию пристеночных областей. В первом, – области, в которых вязкость существенна, – вязкий и буферный слои не разрешаются (заменяются моделью, точкой). Вместо расчета вязких слоев применяется полуэмпирическая формула, называемая пристеночной функцией (или функцией стенки). Эта функция позволяет увязать между собой развитое турбулентное течение и течение в вязкой пристеночной области. Использование функции стенки не требует модификации модели турбулентности для проведения расчетов вблизи стенки. Другой подход основан на модификации модели турбулентности в областях контролируемых вязкостью, для того чтобы непосредственно разрешить (подобно микроскопу с большой разрешающей способностью) течение в вязких слоях, в том числе в вязком подслое.
Рис.5.2. Подходы к моделированию пристеночных областей.
Для большинства высокорейнольдсовых течений функция стенки позволяет существенно экономить компьютерные ресурсы, поскольку нет необходимости рассчитывать контролируемую вязкостью пристеночную область, в которой параметры потока изменяются наиболее быстро. Пристеночная функция является популярным подходом, поскольку экономит компьютерные ресурсы при разумной точности получаемых результатов. Это часто используемая в практике инженерных расчетов функция. Однако, пристеночная функция (функция стенки) становится неадекватной при моделировании низкорейнольдсовых течений. Fluent обеспечивает оба подхода для моделирования пристеночных потоков.
Функции стенки.
Функция стенки представляет собой набор полуэмпирических формул и функций, которые обеспечивают связь переменных решения в полностью турбулентной области с пристеночными ячейками. Под этими функциями понимают: - Закон стенки для средней скорости и температуры; - формулы для параметров пристеночной турбулентности. Fluent предоставляет выбор из двух вариантов функции стенки: - стандартная функция стенки; - неравновесная функция стенки.
Стандартная функция стенки. Эта функция была предложена Лаундером и Сполдингом и наиболее широко используется в инженерных приложениях. Во Fluent’е она включается по умолчанию. Стандартная функция стенки описана во всех деталях в опциях Fluent. Она работает удовлетворительно в широком интервале ограниченных стенками течений. Однако она имеет тенденцию становиться менее надежной, когда ситуация в потоке сильно отклоняется от идеальных условий, которые полагались при ее выводе. Среди прочих, гипотезы о постоянстве сдвиговых напряжений и локальном равновесии сильнее всего ограничивают универсальность стандартной функции стенки. Следовательно, когда пристеночное течение подвергается воздействию сильного градиента давления, и когда течение существенно не равновесно, качество прогноза снижается.
Неравновесная функция стенки. Обладает способностью частично учитывать влияние градиента давления и отклонение от равновесия.
Соотношение между стандартной и неравновесной функциями стенки. Неравновесную функцию рекомендуется применять для сложных течений, включая течения с отрывом и присоединением, а также для потоков с большими градиентами давления и изменениями параметров. Для таких течений может быть получено некоторое улучшение результатов, особенно при определении напряжений на стенках и тепловых потоков.
Ограничение применения функций стенки. Функция стенки дает разумно точные результаты в большинстве случаев высокорейнольдсовых течений, ограниченных стенками. Однако функция стенки становится менее надежной при отклонении от идеальных условий, в которых она была получена. Например: - Низкорейнольдсовые потоки или большое влияние пристеночных эффектов; - Большие потоки через стенку (вдув/отсос); - Большие положительные градиенты давления, приводящие к отрыву пограничного слоя; - Большие массовые силы (при вращении или контролируемые архимедовыми силами потоки); - Высокая степень трехмерности в пристеночном течении (спиральные течения, сильно перекошенные 3D погранслои). Если любая из перечисленных особенностей превалирует в исследуемом течении, и если выявление этой особенности является важным для успешного решения задачи, вы должны использовать пристеночную модель, сочетающуюся с адекватным сеточным разрешением в пристеночной области.
Усовершенствованный пристеночный алгоритм.
Усовершенствованный пристеночный алгоритм – представляет собой метод, сочетающий двухслойную пристеночную модель с усовершенствованной функцией стенки. При этом сетка в пристеночной области должна быть достаточной мелкой для разрешения вязкого подслоя, что обычно достигается при y+»1. Таким образом, EWT идентична традиционным двухзонным моделям. Однако ограничение на достаточную мелкость сетки может привести к значительному увеличению требуемых вычислительных ресурсов. В идеале хотелось бы получить модель, которую можно применять на грубой сетке (обычно обозначаемую как пристеночная сетка), как и на мелкой сетке (низкорейнольдсовые сетки). Дополнительно, не должны возникать чрезмерные ошибки для промежуточных сеток, которые слишком мелки для пристеночных ячеек, лежащих в полностью турбулентной области, но еще достаточно грубы для должного разрешения вязкого подслоя. Для достижения высокой точности, которая является целью при использовании стандартных двухслойных моделей с мелкими сетками, и в то же время, чтобы не снизить значительно точность при использовании сеток, которые применяются для функции стенки, Fluent объединяет двухслойную модель с усовершенствованной функцией стенки.
Двухслойная модель для усовершенствованного пристеночного алгоритма. В двухслойной модели область пограничного слоя разделяется на область контролируемую вязкостью и полностью турбулентную область. Линия раздела двух областей определяется по турбулентному числу Рейнольдса, Rey,
в качестве характерного размера в котором, используется расстояние от стенки до центра рассматриваемой ячейки, у, взятое по нормали к стенке (минимальное расстояние до стенки), а характерная скорость вычисляется как среднеквадратичная пульсационная скорость (k 1/2).
Выбора сетки при моделировании турбулентных течений. Успех в моделировании турбулентных течений требует некоторого анализа при построении сеток. Так как турбулентность (через изменяющуюся по пространству эффективную вязкость) играет доминирующую роль в переносе импульса и других скалярных величин для большинства сложных турбулентных потоков, вы должны быть уверены, в том, что если требуется высокая точность, то характеристики турбулентности должным образом определяются. Благодаря сильному взаимодействию среднего течения и турбулентности, численные результаты для турбулентных потоков имеют значительно большую склонность к сеточной зависимости, нежели ламинарные. Следовательно, для течений, где осредненные параметры изменяются быстро и имеют сдвиговые слои с большими средними скоростями деформациями, необходимо применять достаточно мелкие сетки для обеспечения высокого разрешения. Проверку сетки можно провести путем построения изолиний (display) или графиков (plot) величин y+, y* и Rey, которые доступны при постпроцессинге. Следует помнить, что y+, y* и Rey не являются фиксированными геометрическими величинами, а зависят от результатов решения. Например, когда вы вдвое измельчаете сетку, это не означает, y+ уменьшится в два раза. Для построения сетки в пристеночных областях могут быть применены различные стратегии.
Пристеночная сетка для функции стенки. Расстояние от стенки до центра пристеночной ячейки может быть определено по интервалу, в котором действует логарифмический закон. Это расстояние обычно измеряется в единицах y+=uty/n. - Для стандартной и неравновесной функций стенки все ячейки должны лежать в области 30<y+<300. - Несмотря на то, что Fluent применяет ламинарный закон при y+<11,225, использования чрезмерно мелкой сетки вблизи стенки следует избегать, потому, что функция стенки становится менее точной в этой области. Нужно стремиться к тому, чтобы сетка обеспечивала в смежных со стенкой ячейках значения y+, соответствующие буферной области, т.е. 5<y+<30. - Использование чрезмерного растяжения по нормали к стенке следует избегать. - Важно иметь, по крайней мере, несколько ячеек внутри пограничного слоя.
Рекомендации по построению сетки для усовершенствованного пристеночного алгоритма. Несмотря на то, что усовершенствованный пристеночный алгоритм спроектирован для расширения возможности моделирования на вязкий подслой, нужно конструировать сетку так, чтобы она полностью разрешала область вязкого подслоя. В этом случае требования к сетке таковы. - Если EWT применяется с целью разрешения ламинарного подслоя, y+ в пристеночных ячейках должна иметь значение 1. Допустимы и более высокие значения, если они надежно принадлежат вязкому подслою (y+=4 – 5). - Следует обеспечить, по меньшей мере, 10 ячеек внутри вязкого подслоя, чтобы иметь уверенность в надежном разрешении параметров осредненного течения и турбулентности.
Тема 4. Турбулентные течения. Подходы к моделированию. Характеристики турбулентных потоков. Многообразие турбулентных потоков. Масштабы и подходы к моделированию турбулентных течений. Метод DNS, метод LES, методы RANSE.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.223.136 (0.01 с.) |

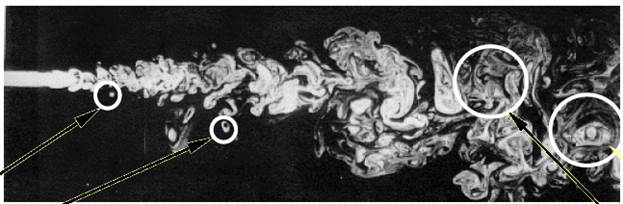
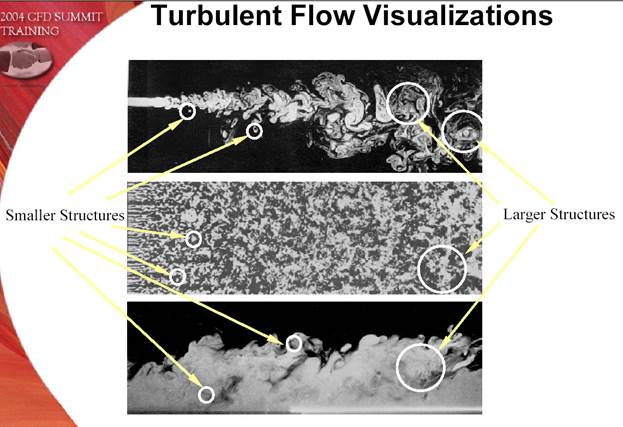
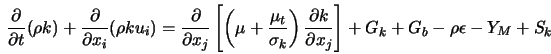
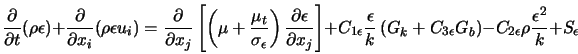

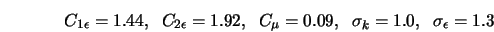
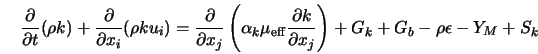
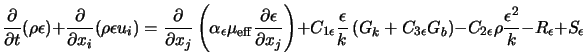
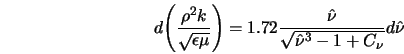
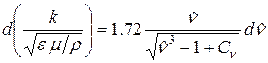
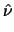
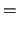
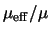

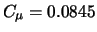
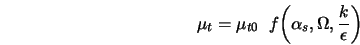
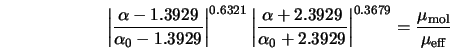
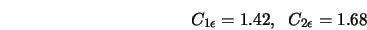


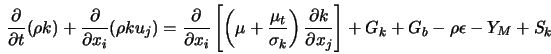


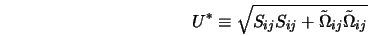
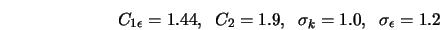

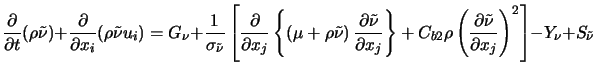
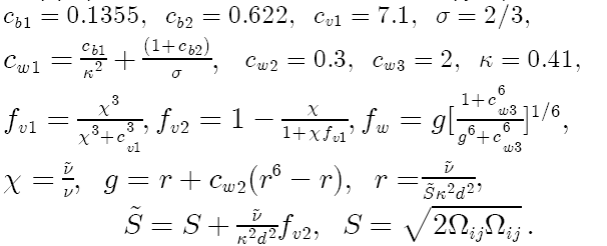
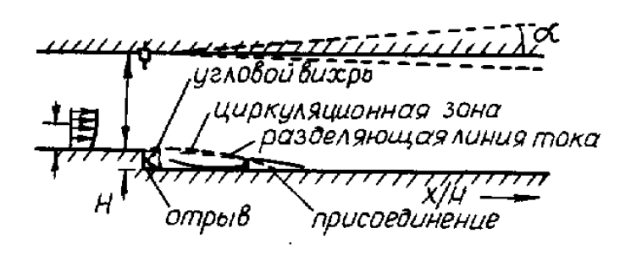
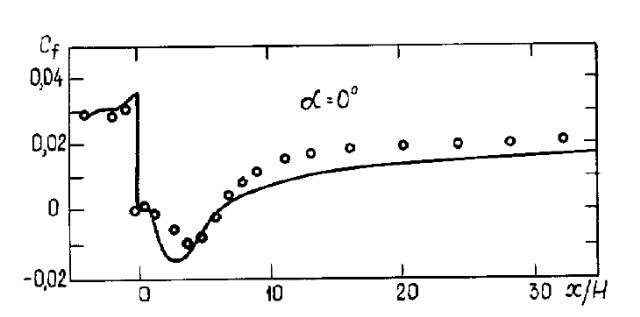
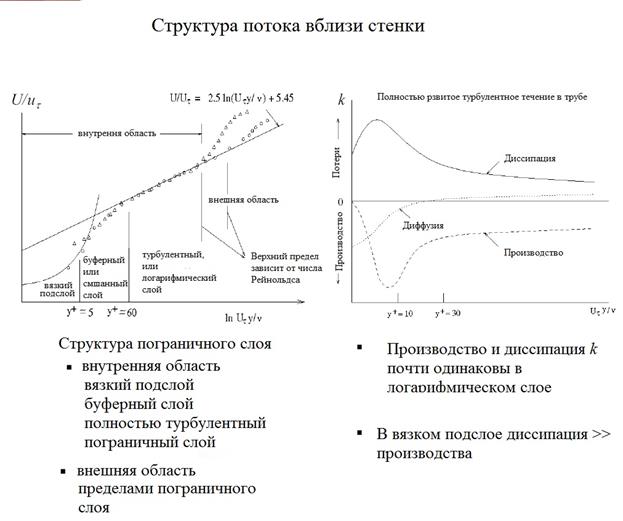 Рис.5.1. Изменение параметров потока в пристеночных областях.
Рис.5.1. Изменение параметров потока в пристеночных областях.
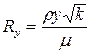 ,
,


