Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналогия между магнитной и электрической цепями.Содержание книги
Поиск на нашем сайте
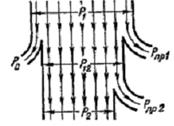
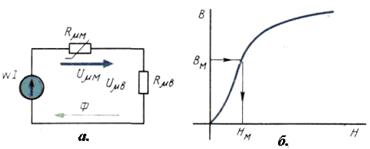
Расчет магнитных цепей производится на основе закона полного тока с помощью уравнений магнитного состояния. Как и в электрических цепях, здесь используют уравнения магнитного состояния: узловое — алгебраическая сумма магнитных потоков, сходящихся в любом узле (поток через замкнутую поверхность), всегда равна нулю: контурное — алгебраическая сумма падений магнитных напряжений в любом замкнутом контуре магнитной цепи равна алгебраической сумме магнитодвижущих сил в контуре: Падение магнитного напряжения на заданном участке магнитной цепи определяют как произведение напряженности магнитного поля на длину участка цепи (или магнитного сопротивления участка на магнитный поток) и выражают в амперах: где Зависимость магнитного потока Ф от магнитодвижущей силы ω I и магнитных сопротивлений Rμ участков магнитной цепи получают из уравнения магнитного состояния ветви магнитной цепи
Между вебер-амперными характеристиками Ф(I) в магнитных цепях и вольт-амперными U(I) в электрических цепях существует полная аналогия. Для магнитной цепи можно изобразить аналогичную режиму нагрузки электрической цепи, схему замещения.
Рис.8. Например, для магнитной цепи рис. 3, б она имеет вид, представленный на рис. 8, а. Схема содержит источник магнитодвижущей силы ω I и два участка с магнитными сопротивлениями Rμм и Rμв. Как и для электрической цепи, можно записать уравнение магнитного состояния где Методы расчета магнитной цепи При расчете магнитной цепи могут быть две задачи: прямая, когда известны геометрические размеры и магнитные свойства материала магнитопровода, а также значение магнитного потока Ф (определяются магнитодвижущая сила и ток I в витках обмотки), и обратная, когда задается магнитодвижущая сила, геометрические размеры и материалы магнитопровода (определяется магнитный поток Ф). Рассмотрим прямую задачу. В неразветвленной и неоднородной магнитной цепи (см. рис. 3, б) известны: значение магнитного потока в воздушном зазоре Ф, геометрические размеры и материал магнитопровода, число витков обмотки ω, а также зависимость Вм(Н) (рис. 8, б). Определить мдс ω I. ПРИМЕР Алгоритм расчета магнитной цепи можно представить в следующем виде: 1. По заданным геометрическим размерам определяем Sм; Sв; lм и lв. 2. По заданному магнитному потоку Ф определяем магнитные индукции Вм, Вв на участках магнитной цепи. Цепь одноконтурная, следовательно, магнитный поток Ф во всех участках цепи будет неизменным. Полагая Sв = Sм получим
3. По вычисленным Вм и кривой намагничивания В(Н) для заданного материала магнитопровода находим Нм (рис. 8, б). 4. Обходя контур в направлении магнитного потока, запишем уравнение магнитного состояния
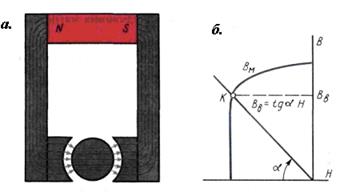
здесь Таким образом, расчетное уравнение примет вид В обратной задаче расчета магнитной цепи задается мдс ω I и требуется определить магнитный поток Ф на участке цепи (или в воздушном зазоре). Из-за нелинейности зависимость Ф (ω I) необходимо предварительно рассчитать и построить, а затем для заданного значения ω I определить Фв. Для построения зависимости Ф(ω I) задают 5—7 значений магнитного потока, по алгоритму «прямой задачи» рассчитывают соответствующие значения мдс и строят зависимости Ф(ω I). Во многих электротехнических устройствах (электрических машинах, трансформаторах и др.) используют симметричные магнитные системы (см. рис. 3, в). В цепи такой системы магнитный поток Ф1 равен потоку Ф2. В среднем сердечнике магнитопровода оба потока Ф1 и Ф2 складываются, но и сечение сердечника вдвое больше сечения крайних сердечников. При расчете такую цепь можно представить как две самостоятельные, если мысленно разделить магнитопровод по вертикальной оси ab. Магнитные потоки Ф1 и Ф2 при таком делении останутся неизменными по направлению. Иными словами, схему замещения магнитной цепи такой магнитной системы можно представить двумя независимыми неразветвленными магнитными цепями, в которых действуют одинаковые мдс, и рассчитывать одну из двух составляющих. При решении прямой задачи, когда задан магнитный поток Ф в любом стержне, полученное значение мдс равно значению полной мдс. При решении обратной задачи значение магнитного потока в среднем стержне Ф1 определяют на основании уравнения состояния узла. Магнитная цепь с постоянными магнитами В магнитных системах с постоянными магнитами поле в воздушном зазоре создается под воздействием энергии постоянного магнита. В качестве примера на рис. 9, а представлена магнитная цепь магнитоэлектрического прибора, состоящая из постоянного магнита, элементов из магнитомягкого материала и двух воздушных зазоров. Схема замещения этой цепи показана на рис. 8. Рис.9. Учитывая, что магнитное сопротивление ферромагнитных элементов мало по сравнению с сопротивлением воздушных зазоров, схема замещения упрощается и уравнение по закону полного тока имеет вид Зная характеристику магнитотвердого материала В(Н) и полагая, что Это уравнение показывает, что зависимость Вв(H) — прямая во втором квадранте (рис. 9, б). Определяем Вв графическим методом. Для этого во втором квадранте строится кривая размагничивания материала В(Н) и из начала осей координат проводится прямая под углом ВАЖНОЕ 1. Ферромагнитные материалы в магнитопроводах электромагнитных устройств усиливают магнитное поле, создаваемое током намагничивающей катушки. 2. Изменение воздушного зазора в магнитопроводе цепи постоянного тока приводит к изменению магнитного потока в рабочем зазоре: с увеличением воздушного зазора магнитный поток уменьшается. 3. Ферромагнитные материалы бывают магнитомягкие с малой коэрцитивной силой (единицы А/см) и магнитотвердые с большой коэрцитивной силой (десятки и сотни А/см). Магнитомягкие материалы используют в магнитопроводах различных электромагнитных устройств; магнитотвердые материалы — для изготовления постоянных магнитов и магнитных систем. 4. Расчет магнитных цепей с ферромагнитными элементами аналогичен расчету электрических цепей постоянного тока с нелинейным элементами. 5. При расчете магнитных цепей, как и электрических, используют узловые и контурные уравнения.
Справочный материал по электрическим машинами трансформаторам Машины постоянного тока Так, из закона электромагнитной индукции следует, что если проводник перемешать перпендикулярно линиям магнитного поля, то в нем будет наводиться эдс,а ее значение определится формулой е = Blυ, где В — магнитная индукция, В∙с/м2; l, υ — длина, м, и скорость, м/с, перемещения проводника. Под действием эдс в проводнике, замкнутом на резистор, возникает ток в направлении, совпадающем с направлением эдс. В результате взаимодействия проводника с током и магнитного поля возникнет электромагнитная сила, которая определяется по формуле Fэм = В Il, а ее направление — по правилу «левой руки». Уравнение электрического состояния генератор а, Е = U + Rя I или U = Е - Rя I
Уравнение электрического состояния двигател я, Е = U - Rя I или U = Е + Rя I Действующее значение эдс в витке Среднее значение эдс в витке в предположении, что Ф=Вср lτ равно Если общее число витков, соединенных последовательно, одной параллельной ветви равно N/(2а), то эдс на щетках где сЕ= pN/(60 a) — конструктивная постоянная обмотки; N — число проводников; а — число параллельных ветвей. Электродвижущая сила одной фазы якорной обмотки где Eв — эдс витка; kоб — обмоточный коэффициент, учитывающий тип обмотки и отличие геометрической суммы эдс витков от арифметической; w — число витков фазы. Внешнии характеристики при различных способах возбуждения генератора Рис.1.
1 Характеристика холостого хода генератора ПТ с независимым возбуждением 2 Внешняя характеристика генератора ПТсо смешанным возбуждением 3 Внешняя характеристика генератора ПТс независимым возбуждением 4 Внешняя характеристика генератора ПТс последовательным возбуждением 5 Внешняя характеристика генератора ПТс параллельным возбуждением
Универсальная характеристика машины параллельного возбуждения Рис.2.
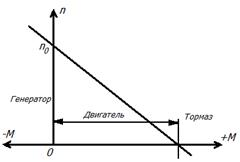
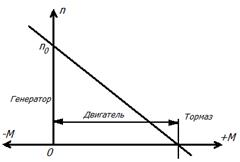
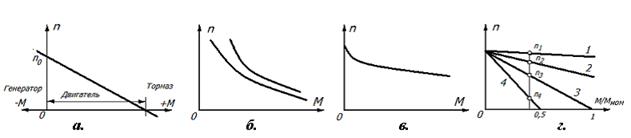
Рис.2 1 - Режим генератора, 2 - Режим двигателя, 3 - Режим электромагнитного тормаза
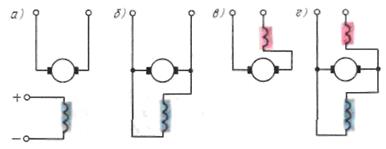
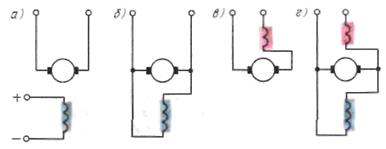
Рис.3. Независимое возбуждение – а; параллельное возбуждение – б; последовательное возбуждение – в; смешанное – г. Д вигатель П остоянного Т ока
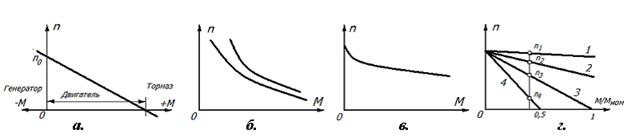
Рис.4. а - универсальная характеристика машины параллельного возбуждения; б - механическая характеристика двигателя последовательного возбуждения; в - механическая характеристика двигателя смешанного возбуждения; г - механическая характеристика двигателя параллельного возбуждения.
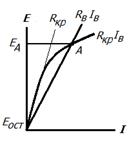
Самовозбуждение генератора происходит при наличи трёх условий 1- Остаточного магнитного потока, создающего Еост 2- Совпадающего направления поля обмотки возбуждения с направлением остаточного магнитного потока 3- Сопротивления обмотки возбуждения (при параллельном возбуждении) меньше критического, т.е. когда ток возбуждения способен достигать значения, обеспечивающего на характеристике холостого хода заданное значение ЕА . (RB >RKP)
Рис.5 Графическое определение режима генератора при самовозбуждении. Синхронный генератор Синхронной называется электрическая машина, частота вращение которой связана постоянным отношением с частотой сети переменного тока, в которую машина включена.
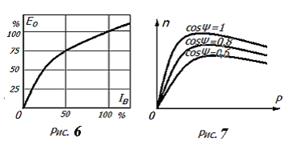
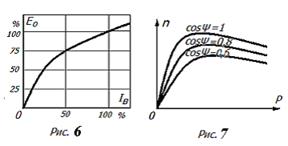
Рис.6. Характеристика холостого хода синхронного генератора или магнитная характеристика (влияние тока возбуждения на ЭДС) Рис.7. Зависимости кпд синхронного генератора от нагрузки при различных коэффициентах мощности Энергетические потери и диаграммы Энергетические потери синхронного генератора делятся на постоянные – механические, возбуждения и в стали, а переменные потери – меди и добавочные КПД синхронного генератора описываются формулой η = 3 UIcosφ/( 3 UIcosφ + Pпост + Pперем)
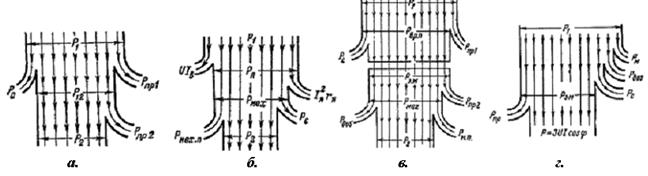
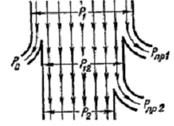
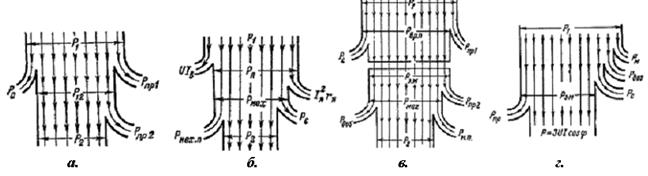
Рис.8 а - энергетическая диаграмма трансформатора; б - энергетическая диаграмма двигателя постоянного тока; в - энергетическая диаграмма асинхронного двигателя; г - энергетическая диаграмма синхронного генератора.
Максимальная частота вращения синхронной машины в сети переменного тока с частотой 50 Гц - 2πf (3000)
Если количество пар полюсов р1>р2, то частотавращения ротора - n1< n2 синхронной машины уменьшится. (n=2πf/ p)
У гидрогенераторов первичным двигателем является гидротурбина, т.к. частота вращения малая, то система возбуждения многополюсная.
У синхронного генератора при многополюсной системе возбуждения – роторы выполняется явнополюсными, а при двухполюсной системе возбуждения – неявнополюсными. Действующее значение эдс фазы якорной обмотки синхронного генератора при синусоидальной форме эдс, индуцируемой в проводах равно Е=4,44 fwkобФо, где w – число витков фазы якорной обмотки; kоб – обмоточный коэффициент.
При ёмкостной и индуктивной нагрузке магнитные линии поля ротора Фо и статора Фа коллинеарны.
Уравнение электрического состояния одной фазы СГ с учетом поля рассеяния якоря Фо имеет вид Е0 + Еа + Еσ = U + Rя I Где Е0 – эдс холостого хода; Еа – эдс самоиндукции обмотки якоря; Еσ – эдс поля рассеяния
Упрощённое уравнение электрического состояния фазы СГ, U = Еа - jXсин I Электромагнитный момент СГ зависит от фазового сдвига, тока и от фазового потока М = CМ ФIcosφ
Трансформаторы
1 - однофазный, 2 – дроссель, 3 - трехфазный, звезда/звезда, 4 - трехфазный, звезда/треугольник, 5 – автотрансформатор. Функциональная связь ЭДС обмотки трансформатора, магнитным потоком, числом витков и частотой - Е1 = 4,44 fwФ1
Рис.2 Опыт холостого хода - а; опыт короткого замыкания - б; опыт номинальной нагрузки – в.
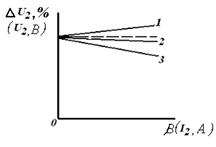
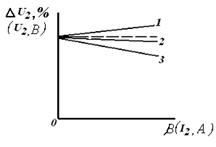
Рис.3. Зависимость изменения напряжения на зажимах вторичной обмотки трансформатора от коэффициента нагрузки: при индуктивной нагрузке трансформатора φ > 0, - 1; при ёмкостной нагрузке трансформатора φ < 0, - 3; внешняя характеристика трансформатора - 2.
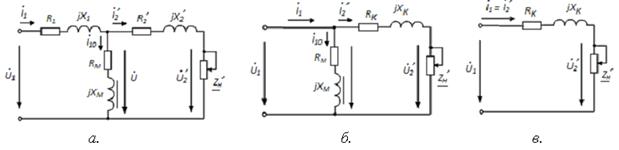
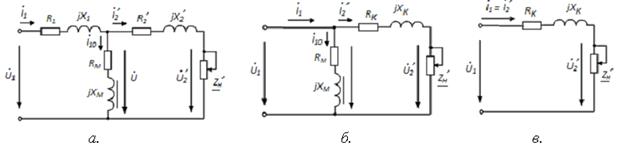
Рис.4. Схемы замещения: Т – образная эквивалентная схема реального трансформатора – а; упрощенная Г – образная схема трансформатора – б; при коротком замыкании – в. Потери мощности трансформатора
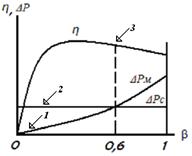
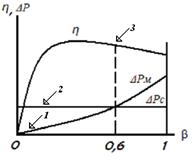
а. б. Рис.2. Потери мощности трансформатора а - в проводах обмотки (меди) – 1, в сердечнике (стали) - 2, зависимость КПД от нагрузки – 3, б - энергетическая диаграмма трансформатора.
Справочный материал по электрическим машинами трансформаторам Машины постоянного тока Так, из закона электромагнитной индукции следует, что если проводник перемешать перпендикулярно линиям магнитного поля, то в нем будет наводиться эдс,а ее значение определится формулой е = Blυ, где В — магнитная индукция, В∙с/м2; l, υ — длина, м, и скорость, м/с, перемещения проводника. Под действием эдс в проводнике, замкнутом на резистор, возникает ток в направлении, совпадающем с направлением эдс. В результате взаимодействия проводника с током и магнитного поля возникнет электромагнитная сила, которая определяется по формуле Fэм = В Il, а ее направление — по правилу «левой руки». Уравнение электрического состояния генератор а, Е = U + Rя I или U = Е - Rя I
Уравнение электрического состояния двигател я, Е = U - Rя I или U = Е + Rя I Действующее значение эдс в витке Среднее значение эдс в витке в предположении, что Ф=Вср lτ равно Если общее число витков, соединенных последовательно, одной параллельной ветви равно N/(2а), то эдс на щетках где сЕ= pN/(60 a) — конструктивная постоянная обмотки; N — число проводников; а — число параллельных ветвей. Электродвижущая сила одной фазы якорной обмотки где Eв — эдс витка; kоб — обмоточный коэффициент, учитывающий тип обмотки и отличие геометрической суммы эдс витков от арифметической; w — число витков фазы. Внешнии характеристики при различных способах возбуждения генератора Рис.1.
1 Характеристика холостого хода генератора ПТ с независимым возбуждением 2 Внешняя характеристика генератора ПТсо смешанным возбуждением 3 Внешняя характеристика генератора ПТс независимым возбуждением 4 Внешняя характеристика генератора ПТс последовательным возбуждением 5 Внешняя характеристика генератора ПТс параллельным возбуждением
Универсальная характеристика машины параллельного возбуждения Рис.2.
Рис.2 1 - Режим генератора, 2 - Режим двигателя, 3 - Режим электромагнитного тормаза
Рис.3. Независимое возбуждение – а; параллельное возбуждение – б; последовательное возбуждение – в; смешанное – г. Д вигатель П остоянного Т ока
Рис.4. а - универсальная характеристика машины параллельного возбуждения; б - механическая характеристика двигателя последовательного возбуждения; в - механическая характеристика двигателя смешанного возбуждения; г - механическая характеристика двигателя параллельного возбуждения.
Самовозбуждение генератора происходит при наличи трёх условий 1- Остаточного магнитного потока, создающего Еост 2- Совпадающего направления поля обмотки возбуждения с направлением остаточного магнитного потока 3- Сопротивления обмотки возбуждения (при параллельном возбуждении) меньше критического, т.е. когда ток возбуждения способен достигать значения, обеспечивающего на характеристике холостого хода заданное значение ЕА . (RB >RKP)
Рис.5 Графическое определение режима генератора при самовозбуждении. Синхронный генератор Синхронной называется электрическая машина, частота вращение которой связана постоянным отношением с частотой сети переменного тока, в которую машина включена.
Рис.6. Характеристика холостого хода синхронного генератора или магнитная характеристика (влияние тока возбуждения на ЭДС) Рис.7. Зависимости кпд синхронного генератора от нагрузки при различных коэффициентах мощности Энергетические потери и диаграммы Энергетические потери синхронного генератора делятся на постоянные – механические, возбуждения и в стали, а переменные потери – меди и добавочные КПД синхронного генератора описываются формулой η = 3 UIcosφ/( 3 UIcosφ + Pпост + Pперем)
Рис.8 а - энергетическая диаграмма трансформатора; б - энергетическая диаграмма двигателя постоянного тока; в - энергетическая диаграмма асинхронного двигателя; г - энергетическая диаграмма синхронного генератора.
Максимальная частота вращения синхронной машины в сети переменного тока с частотой 50 Гц - 2πf (3000)
Если количество пар полюсов р1>р2, то частотавращения ротора - n1< n2 синхронной машины уменьшится. (n=2πf/ p)
У гидрогенераторов первичным двигателем является гидротурбина, т.к. частота вращения малая, то система возбуждения многополюсная.
У синхронного генератора при многополюсной системе возбуждения – роторы выполняется явнополюсными, а при двухполюсной системе возбуждения – неявнополюсными. Действующее значение эдс фазы якорной обмотки синхронного генератора при синусоидальной форме эдс, индуцируемой в проводах равно Е=4,44 fwkобФо, где w – число витков фазы якорной обмотки; kоб – обмоточный коэффициент.
При ёмкостной и индуктивной нагрузке магнитные линии поля ротора Фо и статора Фа коллинеарны.
Уравнение электрического состояния одной фазы СГ с учетом поля рассеяния якоря Фо имеет вид Е0 + Еа + Еσ = U + Rя I Где Е0 – эдс холостого хода; Еа – эдс самоиндукции обмотки якоря; Еσ – эдс поля рассеяния
Упрощённое уравнение электрического состояния фазы СГ, U = Еа - jXсин I Электромагнитный момент СГ зависит от фазового сдвига, тока и от фазового потока М = CМ ФIcosφ
Трансформаторы
1 - однофазный, 2 – дроссель, 3 - трехфазный, звезда/звезда, 4 - трехфазный, звезда/треугольник, 5 – автотрансформатор. Функциональная связь ЭДС обмотки трансформатора, магнитным потоком, числом витков и частотой - Е1 = 4,44 fwФ1
Рис.2 Опыт холостого хода - а; опыт короткого замыкания - б; опыт номинальной нагрузки – в.
Рис.3. Зависимость изменения напряжения на зажимах вторичной обмотки трансформатора от коэффициента нагрузки: при индуктивной нагрузке трансформатора φ > 0, - 1; при ёмкостной нагрузке трансформатора φ < 0, - 3; внешняя характеристика трансформатора - 2.
Рис.4. Схемы замещения: Т – образная эквивалентная схема реального трансформатора – а; упрощенная Г – образная схема трансформатора – б; при коротком замыкании – в. Потери мощности трансформатора
а. б. Рис.2. Потери мощности трансформатора а - в проводах обмотки (меди) – 1, в сердечнике (стали) - 2, зависимость КПД от нагрузки – 3, б - энергетическая диаграмма трансформатора.
|
||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.45.82 (0.007 с.) |

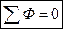
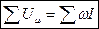
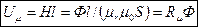 ,
,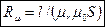 - магнитное сопротивление участка. Для воздушного зазора
- магнитное сопротивление участка. Для воздушного зазора 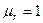 и
и 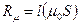 .
.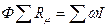 и записывают в виде формулы:
и записывают в виде формулы: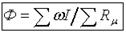
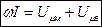
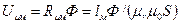 - магнитное напряжение на участке ферромагнетика;
- магнитное напряжение на участке ферромагнетика; 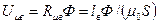 - магнитное напряжение на участке рабочего воздушного зазора.
- магнитное напряжение на участке рабочего воздушного зазора.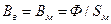
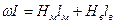

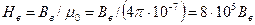 — напряженность магнитного поля в воздушном зазоре.
— напряженность магнитного поля в воздушном зазоре.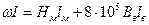
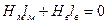
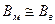 и
и 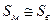 получим
получим 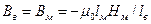
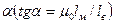 . Точка К пересечения кривой Вм(Н) и прямой
. Точка К пересечения кривой Вм(Н) и прямой  (рис. 9, б) соответствует значению индукции в зазорах Вв и магнитного потока Фв = Bв S.
(рис. 9, б) соответствует значению индукции в зазорах Вв и магнитного потока Фв = Bв S.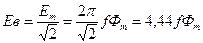
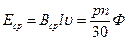
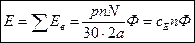 ,
,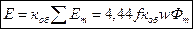
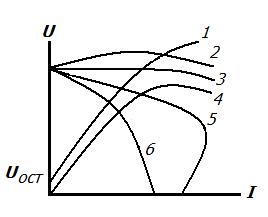 Рис.1.
Рис.1.