Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
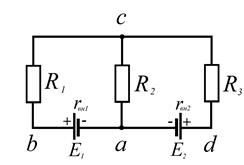
Расчет при помощи закона ома и двух законов КирхгофаСодержание книги
Поиск на нашем сайте
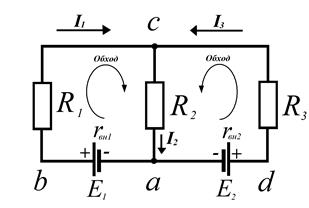
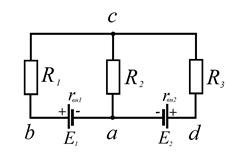
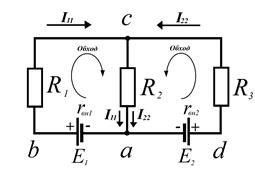
2-ой закон Кирхгофа для 1-го контура:
2-ой закон Кирхгофа для 2-го контура:
1-ый закон Кирхгофа для узла c:
Составим систему уравнений
Преобразуем данную систему
Решим систему уравнений матричным методом
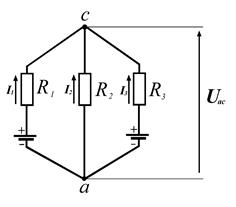
Расчет методом двух узлов (узлового напряжения)
Расчет методом контурных токов
Преобразуем данную систему
Решим систему уравнений матричным методом
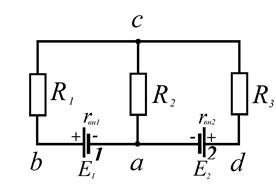
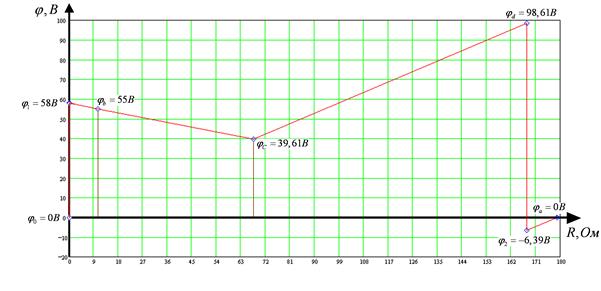
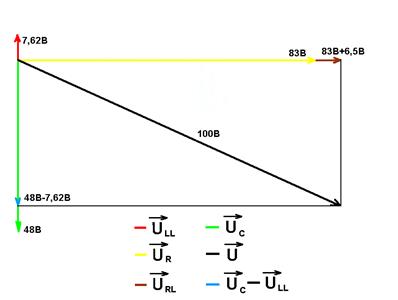
Потенциальная диаграмма для конту ра abcda
Вывод: В ходе данной лабораторной работы мы изучили распределения токов в сложной электрической цепи постоянного тока. Для расчетов использовали законы Кирхгофа для расчета сложной электрической цепи. Также изучили распределение потенциалов и отобразили это в построенной потенциальной диаграммы для одного из замкнутых контуров сложной цепи для определения напряжений в цепи. Изучили влияние внутреннего сопротивления источника ЭДС на режим работы электрической цепи. Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Алтайский государственный технический университет им. И.И.Ползунова» Кафедра общей электротехники
Лабораторная работа №4
«ИССЛЕДОВАНИЕ НЕРАЗВЕТВЛЕННОЙ ЦЕПИ ОДНОФАЗНОГО ПЕРЕМЕННОГО ТОКА»
Работу выполнил: ст-т гр. ПКМ-31 Новиковский Е.А. Работу проверил: Коротких В.М. Оценка_______________
Барнаул 2010 ЦЕЛЬ РАБОТЫ 1. Исследовать явления, происходящие в цепи переменного тока при последовательном соединении элементов. 2. Научиться вычислять параметры цепи. 3. Научиться анализировать работу цепи с помощью построенных по данным опыта векторных диаграмм напряжений и тока.
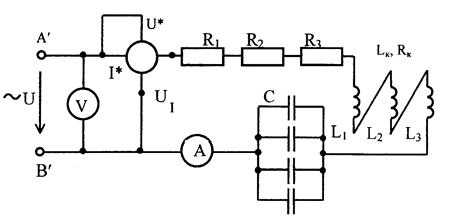
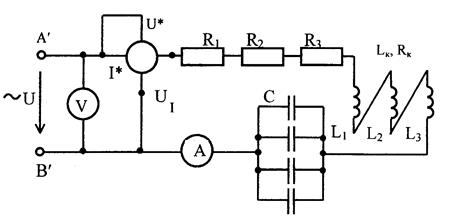
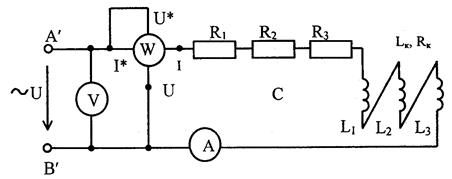
ПРИБОРЫ И ОБОРУДОВАНИЕ 1. Регулируемый источник напряжения переменного тока (клеммы А', В'); 2. Резисторы R1, R2, R3; 3. Индуктивные катушки L1 L2, L3; 4. Батарея конденсаторов С; 5. Ваттметр; 6. Амперметр; 7. Вольтметр; 8. Монтажные провода - 13 шт., провода для подключения вольтметра - 2 шт., щуп для подключения амперметра.
ПРОГРАММА РАБОТЫ И УКАЗАНИЯ К ЕЕ ВЫПОЛНЕНИЮ 1.Перед выполнением работы определить расположение источника питания с регулятором напряжения, измерительных приборов, других элементов цепи, необходимых для работы. 2.Собрать электрическую цепь по схеме, приведенной на рисунке 1, соединив между собой все три катушки последовательно и согласно.
Рисунок 1 Примечание: до подачи питания в цепь убедиться, что регулятор напряжения установлен на нулевой отметке.
3. После проверки цепи преподавателем включить сетевое напряжение стенда и напряжение питания цепи. Установить с помощью регулятора переменного напряжения ток в цепи I = 0,5 А (по амперметру, включенному в цепь). Ваттметром измерить мощность, потребляемую цепью, вольтметром измерить напряжение U, подводимое к цепи, и напряжения на отдельных элементах - UR, UK, UС; результаты измерений записать в таблицу 1 (опыт 1). Таблица 1
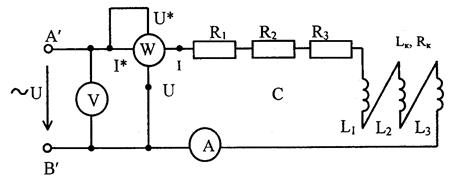
Примечание: после каждого опыта регулятор напряжения доводить до нулевой отметки и отключать напряжение цепи. 4. Из схемы, изображенной на рисунке 1, исключить батарею конденсаторов. Схема принимает вид согласно рисунку 2.
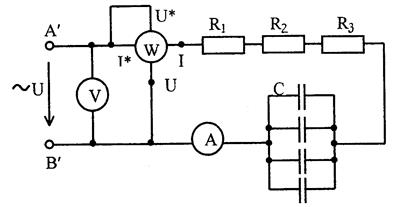
Рисунок 2 5. Собрать электрическую цепь согласно схеме, приведенной на рисунке 2, и после проверки ее преподавателем провести измерения мощности и напряжений при токе 1=0,5 А. Данные измерений занести в таблицу 1 (опыт 2). 6. Из схемы, изображенной на рисунке 1, исключить индуктивные катушки. Схема принимает вид, как показано на рисунке 3.
Рисунок 3 7. Собрать электрическую цепь согласно схеме, приведенной на рисунке 3, и после проверки ее преподавателем провести измерения мощности, напряжений при токе в цепи 1 = 0,5 А. Данные измерений занести в таблицу 1 (опыт 3). 8. Регулятор напряжения установить на нуль, источник напряжения и стенд выключить, данные всех измерений показать преподавателю и, в случае их достоверности, разобрать цепь. 9. Пользуясь соответствующими формулами, рассчитать: а) коэффициент мощности cosφ и угол сдвига фаз φ всей цепи; б) коэффициент мощности cosφк и угол сдвига фаз φк индуктивных катушек; в) полное сопротивление Zк активное сопротивление Rк, индуктивное сопротивление ХL и индуктивность Lк индуктивных катушек; г) активное сопротивление резисторов R; д) емкостное сопротивление Хс и емкость С батареи конденсаторов. Данные расчетов занести в таблицу 2. Таблица 2
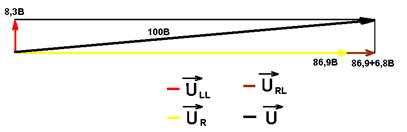
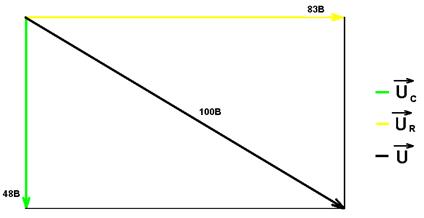
10. Построить в масштабе векторные диаграммы напряжений и тока для всех опытов.
Теоретическая часть Электрическая цепь переменного тока, так же как и цепь постоянного тока, содержит проводники, по которым перемещаются электрические заряды. Количество зарядов, проходящих через сечение проводника в единицу времени называется величиной электрического тока. Она зависит от физических свойств и геометрических размеров проводника, а также от разности потенциалов. Связь между этими величинами называется законом Ома. Закон Ома справедлив всегда, поэтому для любого проводящего участка электрической цепи в любой момент времени можно написать
где u и i - падение напряжения и ток, а r = 1/ g и g = 1/ r - постоянные коэффициенты, называемые сопротивлением и проводимостью данного участка. Величина сопротивления определяется коэффициентом, зависящим от свойств проводящей среды и называемым удельным сопротивлением r, а также длиной l и площадью поперечного сечения s участка, в виде r = r l / s. Сопротивление измеряют в омах [Ом], а обратную ему величину проводимость g в сименсах [См]. Пусть ток в цепи с сопротивлением r изменяется по закону ir = Im sin(w t +y i). Тогда в соответствии с выражением (1) падение напряжения в ней будет
Отсюда следует, что начальные фазы тока и напряжения на этом участке одинаковы y i = y u, а амплитуда напряжения равна Um = rIm. Временные диаграммы, соответствующие выражению (2) приведены на рис. 1 а). Там же показано изображение сопротивления на электрических схемах с условно положительными направлениями тока и напряжения. Амплитудные и действующие значения синусоидальных величин связаны между собой постоянным коэффициентом, поэтому для действующих значений тока и напряжения на сопротивлении можно написать U = rI или I = U/r = gU. Синусоидальные функции выражения (2) можно заменить комплексными числами
и изобразить их на векторной диаграмме рис. 1б) с соответствующим представлением на схеме. Падение напряжения, вызванное протеканием тока, возникает на всех участках электрической цепи. Однако при расчетах его принято изображать отдельным элементом называемым сопротивлением или резистором. В электрических цепях с синусоидальными переменными токами и напряжениями помимо статических явлений, свойственных цепям постоянного тока, появляются динамические эффекты, т.е. эффекты связанные с изменением этих величин во времени. Так на любом участке электрической цепи, по которому протекает переменный ток будет действовать ЭДС самоиндукции eL, наводимая изменяющимся во времени магнитным потоком и равная
Магнитный поток обязательно охватывает все участки электрической цепи, следовательно, при переменном токе на всех участках будет возникать дополнительное падение напряжения
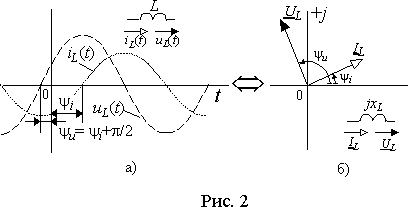
где величина xL =w L, имеющая размерность сопротивления, называется индуктивным сопротивлением. Амплитуда напряжения, возникающего за счет ЭДС самоиндукции, равна Um=xLIm, а его начальная фаза y u = y i +p /2 больше начальной фазы протекающего тока на p /2, т.е. напряжение опережает по фазе ток на 90°. Временные диаграммы, соответствующие выражению (5), приведены на рис. 2 а). Из выражения для амплитуды падения напряжения на индуктивности можно определить его действующее значение UL = xLIL или действующее значение тока IL = UL / xL = bLIL, где bL =1/ xL называется индуктивной проводимостью. Индуктивное сопротивление по сути своей является распределенным параметром, т.к. магнитный поток существует везде, где протекает электрический ток, и на всех участках электрической цепи будет наводиться ЭДС самоиндукции, пропорциональная соответствующему индуктивному сопротивлению. Однако на практике индуктивность всей цепи или отдельного участка считают сосредоточенной в отдельном элементе, изображаемом на схемах в виде рис. 2 а). Выражение (5) можно представить через символические комплексные числа в виде:
где ZL = jxL = xLe jp /2 - комплексное индуктивное сопротивление. Векторная диаграмма и схема замещения для выражения (6) приведены на рис. 2 б). Из выражения (6) можно определить комплексное значение тока через падение напряжения
где YL =1/ ZL =1/ jxL = - jbL = bLe - jp /2 - комплексная индуктивная проводимость.
Из курса физики известно, что заряд уединенного проводящего тела q пропорционален его потенциалу u, т.е. q = Cu. Коэффициент пропорциональности C между зарядом и потенциалом называется емкостью и при неизменных геометрических размерах и свойствах среды является константой. Емкость измеряется в фарадах [Ф]. Фарада является слишком крупной величиной, поэтому для практических целей пользуются ее десятичными долями: микро-, нано- и пикофарадами (10 -6, 10 -9 и 10 -12 Ф). Если за бесконечно малый промежуток времени dt заряд тела изменился на величину dq, то изменение потенциала за этот же интервал времени составит du = dq / C или dq = Cdu. Отнесем изменение заряда к промежутку времени, за который оно произошло. Тогда с учетом того, что электрический ток есть скорость изменения заряда, т.е. i = dq / dt, получим
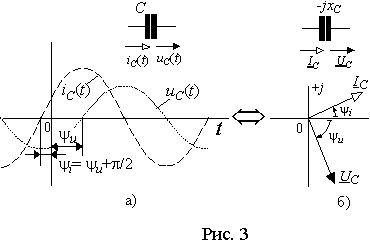
Пусть напряжение на емкости изменяется во времени по синусоидальному закону uС = Um sin(w t +y u). Тогда из выражения (8) ток в емкости определится в виде
Произведение bC = w C имеет размерность проводимости [1/Ом=См] и называется емкостной проводимостью. Отсюда амплитуда тока Im = bCUm, а его начальная фаза y i = y u + p /2. Таким образом, ток в емкости опережает падение напряжения на ней на 90°. Временные диаграммы, соответствующие этим соотношениям тока и напряжения на емкости приведены на рис. 3 а). Пользуясь связью между амплитудными и действующими значениями, для действующих значений тока и падения напряжения на емкости можно записать IС = bCUС или UC = IC / bC = xCIC, где величина xC =1/ bC называется емкостным сопротивлением. При описании электромагнитных процессов в электрических цепях часто требуется выражение для мгновенного значения напряжения на емкости. Его можно получить из выражения (8) в виде
Из выражения (8) следует, что всякое изменение потенциалов в электрической цепи будет вызывать появление токов, приводящих к перераспределению зарядов. Причем, под токами в этом процессе следует понимать как токи проводимости, так и токи смещения, возникающие между всеми участках цепи. Поэтому емкостная проводимость, как и емкость, является распределенным параметром, но для расчетов ее, аналогично индуктивности, представляют сосредоточенной в отдельном элементе, который изображается на схеме в виде рис. 3 а). Связь между напряжением и током в емкости можно представить также комплексными числами и соответствующими векторами (рис. 3 б)) в виде
где YC = jbC = bCe jp /2 - комплексная емкостная проводимость. Отсюда можно также определить комплексное падение напряжения на емкости
где ZC =1/ YC =1/ jbC = - jxC = xCe - jp /2 - комплексное емкостное сопротивление. Индуктивность L и емкость C называются реактивными элементами электрической цепи. Реактивными называются также соответствующие сопротивления и проводимости. Это связано с тем, что падение напряжения на индуктивности и ток через емкость появляются только как следствие или реакция на изменение тока или разности потенциалов. В резисторе падение напряжения не связано с изменением тока, поэтому его сопротивление, в отличие от реактивного, называется активным или резистивным Практическая часть
Расчеты I. Опыт № 1.
Рисунок 1. 1) Вычисление
2) Вычисление
3) Вычисление
II. Опыт № 2.
Рисунок 2. 1) Вычисление
2) Вычисление
III. Опыт № 3.
Рисунок 2. 1) Вычисление
2) Вычисление
Вывод: В ходе данной лабораторной работы … Магнитные цепи Магнитные величины В магнитном поле как особом состоянии среды распределение энергии обусловлено движением электрических зарядов или изменением электрического поля, т. е. электрическим током. Направление магнитного потока определяют по направлению магнитной стрелки, помещенной в это поле. Магнитное поле представляется в виде направленного магнитного потока Ф, линии которого всегда замкнуты. В качестве физической величины, характеризующей интенсивность магнитного потока Ф, служит векор магнитной индукции В, направление которого совпадает с направлением магнитного потока. Единицей магнитного потока в системе СИ является вебер (Вб); 1 Вб = 1 В∙с. За единицу магнитной индукции принимают индукцию, при которой через площадь s в 1 м2, расположенную перпендикулярно направлению магнитного потока, проходит поток в 1 Вб. Магнитную индукцию выражают в теслах (Тл): 1 Тл = 1 Вб/м2 = 1 В·с/м2. Способность источника магнитного поля (электрического тока) создавать магнитный поток характеризуется напряженностью магнитного поля Н, выражаемой в А/м.
Рис.1 В воздухе направление векторов магнитной индукции Количественные соотношения, характеризующие магнитное поле, основаны на законе полного тока. Этот закон устанавливает связь между напряженностью магнитного поля Н в любой точке замкнутого контура вокруг проводника с током I. Например, напряженность в точке А (рис. 1, а) равна где 2π r - длина контура, охватывающего проводник, r - радиус контура. Если действует п проводников с током I, то напряженность в точке А равна: Н = п I/(2π r). Напряженность поля в центре однослойной катушки (когда l>> r)(рис. 1, б) с числом витков ω равна H= ωI/ l. Произведение ωI называют магнитодвижущей силой (мдс) и выражают в амперах. Потокосцепление катушки: ψ=ωФ. В линейной катушке индуктивности потокосцепление пропорционально току. Коэффициент пропорциональности L= ψ/ I называют индуктивностью. Единица индуктивности — генри (Гн). На практике применяют доли; милли- и микрогенри: 1 мГн = 10- 3 Гн; 1 мкГн = 10-6 Гн.
Энергия магнитного поля катушки индуктивности (Дж) определяется работой, совершаемой электрическим током в процессе создания магнитного поля: Магнитные цепи Классификация магнитных цепей. Элементы магнитной цепи. Магнитная система является одним из основных элементов электрических машин и ряда электротехнических устройств. В магнитную систему входят источники магнитного поля (обмотка с током, возбуждающая магнитное поле, постоянный магнит) и система магнитопроводов из ферромагнитного материала, по которым замыкается магнитный поток. При анализе магнитных цепей магнитную систему электротехнического устройства представляют, как и в электрических цепях, эквивалентной схемой. Магнитные цепи бывают неразветвленные и разветвленные, однородные и неоднородные, симметричные и несимметричные. Неразветвленной магнитной цепью называют цепь, через элементы которой замыкается один и тот же магнитный поток. В разветвленной магнитной цепи содержатся ветви, в каждой из которых замыкаются свои магнитные потоки. В однородной магнитной цепи, образованной замкнутым магиитопроводом, магнитный поток находится в однородной среде. Неоднородной называют магнитную цепь, состоящую из участков, имеющих разные сечения, воздушные зазоры, ферромагнитные тела с различными магнитными свойствами. Из физики известна способность вещества под воздействием напряженности внешнего магнитного поля Н создавать собственное поле, называемое намагниченностью М, которая характеризуется магнитной восприимчивостью χ:
где Вещества, имеющие высокое значение магнитной восприимчивости, называют ферромагнитными, или магнитными. К ним относятся железо (Fe), кобальт (Со), никель (Ni), редкоземельные элементы: гадолиний (Gd), диспрозий (Dy) и др., а также сплавы на базе этих элементов.
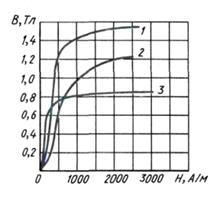
Зависимость магнитной индукции в веществе (материале) от напряженности внешнего магнитного поля В(Н) носит нелинейный характер: по мере увеличения Н индукция В сначала возрастает резко, а затем, приближаясь к области насыщения, процесс намагничивания материала замедляется и прекращается, когда резервы ферромагнетика оказываются исчерпанными Рис.2.
Рис.2.
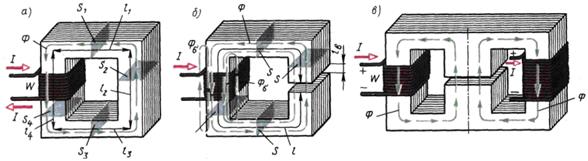
Рис.3. а – однородная неразветвлённая; б – неоднородная неразветвлённая; в - неоднородная разветвлённая.
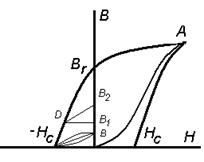
Если элемент магнитной цепи, например цилиндр из ферромагнитного материала, поместить в однородное магнитное поле, он намагнитится. Если после намагничивания до состояния насыщения внешнее поле убрать (уменьшить до нуля), то цилиндр явится источником магнитного поля за счет намагниченности материала — остаточной намагниченности. Чтобы разрушить эту остаточную намагниченность, нужно создать внешнее поле, направленное противоположно полю, создаваемому цилиндром, для преодоления задерживающей, так называемой коэрцитивной силы Нс, которая стремится сохранить созданную микротоками намагниченность. В зависимости от значения коэрцитивной силы Нс все магнитные материалы принято делить на магнитомягкие и магнитотвердые. Магнитомягкие материалы имеют малую коэрцитивную силу (крутоподнимающаяся основная кривая намагничивания и относительно малая площадь петли гистерезиса) Рис.6.
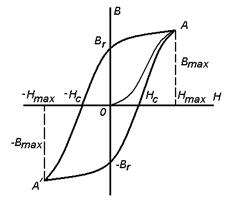
Петля циклического перемагничивания. Явление запаздывания В от Н – магнитный гистерезис.
Рис.4. Нс - остаточная намагниченность (значение напряженности для полного размагничивания сердечника) коэрцитивная сила, В r - остаточная магнитная индукция
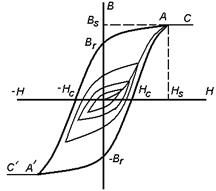
Рис.5. АС и АС – предельная петля гистерезиса
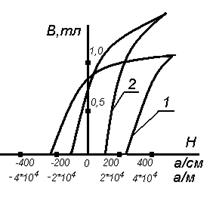
Рис.6. Разные материалы с одной скоростью перемагничивания. 1 - магнитножесткие материалы – с большими значениями коэрцитивной силой (Нс – более 40 а/см) и остаточной магнитной индукцией Вr – 1; 2 – магнитномягкие (малая коэрцитивная сила –от единиц до десятков ампер и высокая магнитная проницаемость с малыми потерями на перемагничивание)
Рис.7. Частные циклы перемагничивания. Коэф. возврата В2 – В1/ В1 – D Расчет магнитной цепи
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.57 (0.011 с.) |

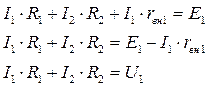
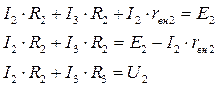
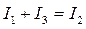
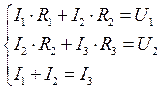
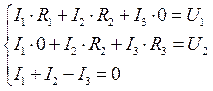
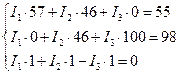
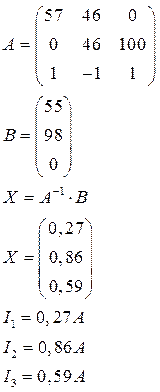
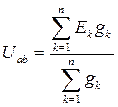
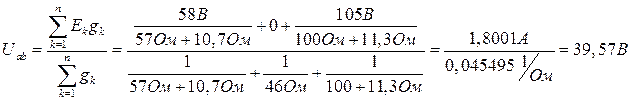
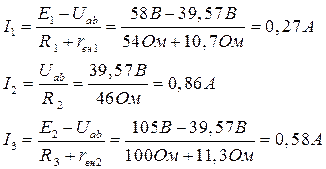
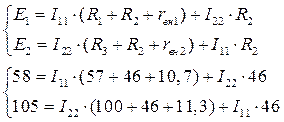
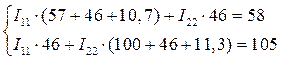
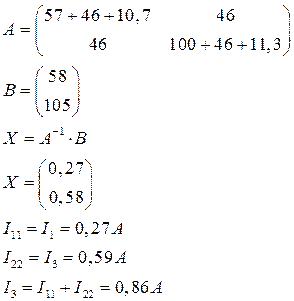
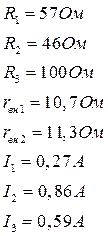
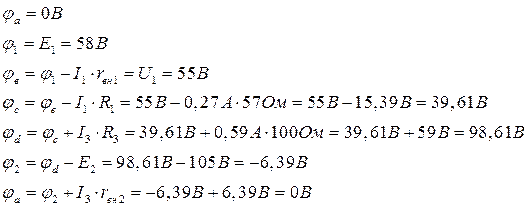

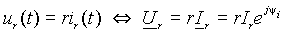
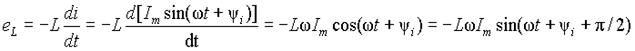 .
.
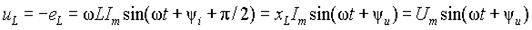 ,
,
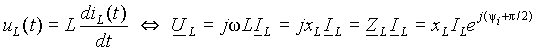 ,
,
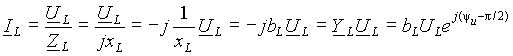 ,
,
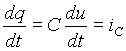 .
.
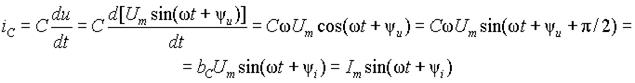 .
.
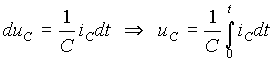 .
.
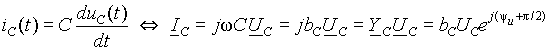 ,
,
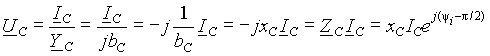 ,
,
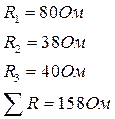
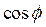 ,
, 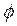 и R
и R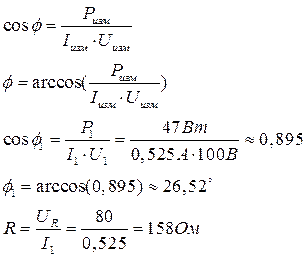
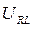 ,
, 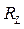 ,
, 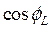 ,
, 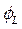 ,
, 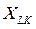 и
и 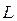
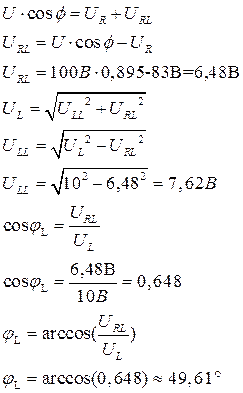
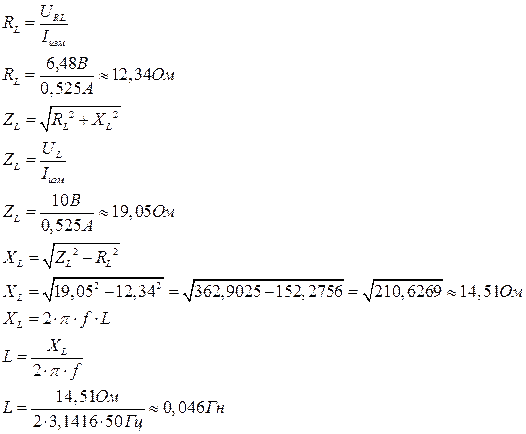
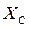 и
и 
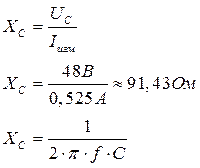

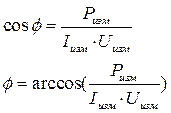
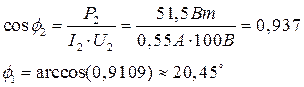
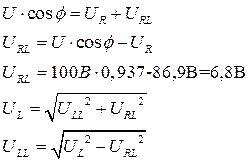
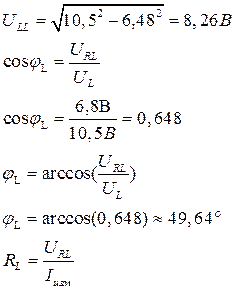
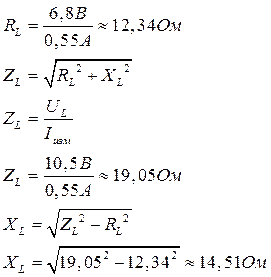

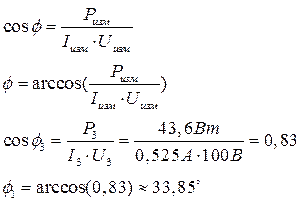
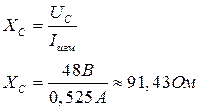
 № опыта
№ опыта
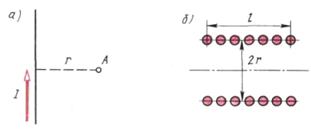
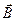 и напряженности магнитного поля
и напряженности магнитного поля 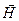 совпадают и связаны соотношением Н = В/μ0, где μ0=4π∙10-7 Гн/м - магнитная постоянная.
совпадают и связаны соотношением Н = В/μ0, где μ0=4π∙10-7 Гн/м - магнитная постоянная.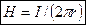
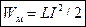
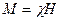 . При этом магнитная индукция в веществе
. При этом магнитная индукция в веществе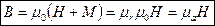
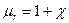 .
. 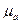 - относительная и абсолютная магнитные проницаемости, соответственно.
- относительная и абсолютная магнитные проницаемости, соответственно.