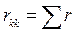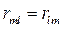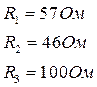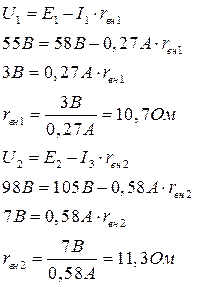Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение закона ома и законов Кирхгофа для расчетов электрических цепейСодержание книги
Поиск на нашем сайте
При помощи закона Ома и двух законов Кирхгофа можно рассчитать режим работы электрической цепи любой сложности. Общей задачей расчета является определение токов во всех участках цепи при заданных параметрах элементов цепи и известной конфигурации цепи. Для составления уравнений по закону Ома и двум законам Кирхгофа следует прежде всего выбрать (произвольно) положительные направления токов во всех ветвях рассчитываемой электрической цепи.
При составлении уравнений на основании второго закона Кирхгофа необходимо также получить независимую систему. В частности, Рис 1. Такие контуры называются независимыми контурами, так как их уравнения взаимно независимы. Число неизвестных токов равно числу ветвей в. Для определения этих токов необходимо составить в независимых уравнений. Так как по первому закону Кирхгофа составляется у -1 независимых уравнений, то на основании второго закона Кирхгофа должно быть составлено в - (у- 1) уравнений. Например, для цепи по рисунку сверху можно было бы составить два уравнения на основании первого закона Кирхгофа для двух узлов (выбранные положительные направления токов показаны стрелками). Для узла 1:
для узла 2:
На основании второго закона Кирхгофа и закона Ома можно было бы составить три уравнения для трех контуров. Для контура 1:
для контура 2:
для контура 3:
Но схема цепи по рисунку содержит только три ветви, т. е. для ее расчета необходимы три независимых уравнения. Для этой схемы число узлов у = 2, т. е. по первому закону Кирхгофа должно быть составлено только одно независимое уравнение: 1 или 2. Действительно, одно из этих уравнений получается из другого умножением на —1. Из трех контуров на рисунке независимыми можно, например, считать 1-й и 2-й (во 2-й входит ветвь 2, которую не содержит 1-й контур). Действительно, уравнение 5 можно получить, составив соответственно разности правых и левых частей уравнений 3 и 4. В качестве независимых для схемы цепи по рисунку можно взять и любую другую пару контуров. Для планарных схем, т. е. тех, которые можно изобразить на чертеже без пересекающихся ветвей, независимая система уравнений по второму закону Кирхгофа получается, в частности, если для записи уравнений выбрать ячейки — контуры, не охватывающие ветвей, которые не входят в эти контуры. Так, схема цепи на рисунке планарная, 1-й и 2-й контуры - ячейки, а 3-й контур охватывает ветвь 3, которая не входит в этот контур. После совместного решения системы независимых уравнений определяются токи в ветвях цепи. Если для какого-либо тока будет получено отрицательное значение, то из этого следует, что его действительное направление противоположно выбранному положительному направлению.
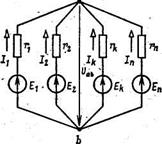
МЕТОД ДВУХ УЗЛОВ Часто исследуемая электрическая цепь содержит только два узла или легко может быть преобразована в подобную цепь. Наиболее простым методом расчета в этом случае является метод двух узлов (узлового напряжения). На рис. 2 показана схема цепи с двумя узлами а и b, состоящая из п ветвей. Так как ветви между узлами а и b соединены параллельно, то разность потенциалов или напряжение между этими узлами можно выразить через ЭДС Ек, ток 1к и сопротивление резистивного элемента r к любой из ветвей. По обобщенному закону Ома:
Откуда:
где Uab — узловое напряжение цепи. На основании этих соотношений ток
В схеме цепи (рис.2) было принято, что все ЭДС направлены к одному из узлов цепи (к узлу а) и положительное направление каждого тока совпадает с направлением ЭДС в ветви, т. е. все токи направлены к тому же узлу. В действительности, конечно, некоторые ЭДС могут быть направлены к узлу b. В этом случае при расчете токов в ветвях с теми же положительными направлениями (к узлу а) по (6) значения ЭДС, действующих к узлу b, должны быть записаны со знаком минус.
и, следовательно,
откуда узловое напряжение определяется через параметры элементов цепи:
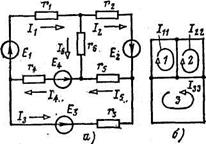
здесь со знаком плюс записываются ЭДС, действующие к узлу а. Зная напряжение между узлами, по (6) легко определить ток в любой ветви. МЕТОД КОНТУРНЫХ ТОКОВ Этот метод может быть применен для расчета любой линейной цепи. Его применение позволяет уменьшить число совместно решаемых уравнений по сравнению с числом уравнений, составляемых по законам Кирхгофа. Для расчета методом контурных токов в сложной электрической цепи (рис. 3, а) независимые контуры выбираются так же как и при составлении уравнений по второму закону Кирхгофа, например контуры-ячейки (рис. 3, б). Затем в каждом из контуров произвольно выбирается положительное направление контурного тока (один и тот же ток во всех ветвях соответствующего контура). Расчетную величину — контурный ток обозначим по номеру контура с двойным индексом, например Ikk. Токи в общих для двух или более контуров ветвях определяются на основании первого закона Кирхгофа как алгебраические суммы соответствующих контурных токов. Алгебраическая сумма ЭДС всех ветвей, входящих в каждый из выбранных независимых контуров, называется контурной ЭДС Ekk (с двойным индексом номера контура), т. е. для любого k -гoконтура
В выражении (7) все ЭДС ветвей, направление которых совпадает (не совпадает) с направлением обхода контура, записываются со знаком плюс (минус). Арифметическая сумма сопротивлений всех резистивных элементов, входящих в каждый из выбранных контуров, называется собственным контурным сопротивлением rkk (с двойным индексом номера контура), т. е.
Арифметическая сумма сопротивлений резистивных элементов, находящихся в общих ветвях двух контуров m и /, называется общим сопротивлением этих контуров, причем, очевидно,
Рис. 3 ПРАКТИЧЕСКАЯ ЧАСТЬ
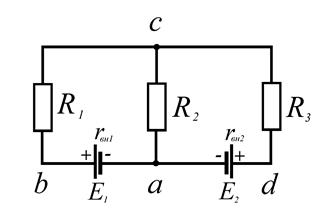
Найдем внутренние сопротивления источников:
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 87; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.9.183 (0.008 с.) |

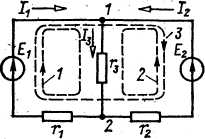 При записи уравнений для узлов цепи по первому закону Кирхгофа необходимо иметь в виду, что число независимых уравнений на единицу меньше общего числа узлов y,т. е. нужно доставить у -1 уравнений. Действительно, если составить уравнения для всех у узлов, то ток каждой ветви войдет дважды в уравнения для узлов, так как ветвь соединяет два узла, причем с противоположными знаками (ток каждой ветви направлен к одному из узлов, и, следовательно, направлен от другого узла). При суммировании всех левых частей уравнений, составленных по первому закону Кирхгофа, получается тождественно нуль.
При записи уравнений для узлов цепи по первому закону Кирхгофа необходимо иметь в виду, что число независимых уравнений на единицу меньше общего числа узлов y,т. е. нужно доставить у -1 уравнений. Действительно, если составить уравнения для всех у узлов, то ток каждой ветви войдет дважды в уравнения для узлов, так как ветвь соединяет два узла, причем с противоположными знаками (ток каждой ветви направлен к одному из узлов, и, следовательно, направлен от другого узла). При суммировании всех левых частей уравнений, составленных по первому закону Кирхгофа, получается тождественно нуль.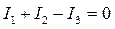 (1)
(1) 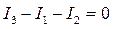 (2)
(2)  (3)
(3) 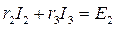 (4)
(4) 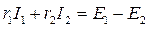 (5)
(5) 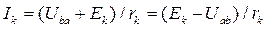
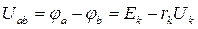
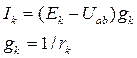 (6)
(6) По первому закону Кирхгофа алгебраическая сумма токов в узле цепи равна нулю, т. е.
По первому закону Кирхгофа алгебраическая сумма токов в узле цепи равна нулю, т. е.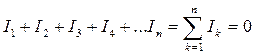
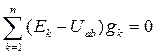 Рис. 2.
Рис. 2.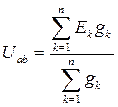
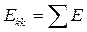 (7)
(7)