Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение матриц проведения экспериментаСодержание книги
Поиск на нашем сайте
Формально прием построения матрицы планирования сводится к методу чередования знаков уровней. Проведение факторного эксперимента осуществляют по следующему алгоритму: – строят матрицу планирования; – ставят опыты в соответствии с планом матрицы; – рассчитывают коэффициенты линейного полинома (уравнение регрессии); – рассчитывают ошибку опыта; – проверяют значимость коэффициентов регрессии; – находят оптимальное решение процесса. Коэффициенты уравнения регрессии в линейной форме рассчитывают по формуле:
где
где m – число параллельных опытов. Формулы (3.4.) и (3.5) можно соединить:
Расчет ошибки опыта оценивают по параллельным опытам:
Построчные ошибки опыта S усредняют:
Для оценки влияния факторов на переменную состояния проводят проверку значимости каждого коэффициента: – находят дисперсию коэффициентов регрессии:
т.е. дисперсии всех коэффициентов равны, т.к. зависят только от ошибки опыта – определяют параметр tip где – из табл. 3.2 определяют критерий Стьюдента по числу степеней свободы
– сопоставляют t ip и tT (табл. 3.2). Таблица 3.2 Процентные точки распределения Стьюдента при уровне
Коэффициент значим при выполнении условия ti p > tT (3.12).
При выполнении условия значимости коэффициент принимают равным 0. Пригодность линейного уравнения для решения задачи поиска области оптимума проверяют по критерию Фишера(табл. 3.3). Для этого сравнивают дисперсии средних опытных данных переменной состояния
где N – число строк матрицы планирования; l – число членов в уравнении регрессии, оставшихся после оценки значимости коэффициента. Согласно критерия Фишера уравнение адекватно описывает процесс при соблюдении следующего условия: F p < F T, (3.14) где F – критерий Фишера, найденный из таблиц для степеней свободы (табл. 3.3) f ад = N - 1 и f о = N (m - 1); F р – расчетное значение критерия: Таблица 3.3 Критерий Фишера при уровне значимости q =0.05
Поиск области оптимума осуществляют методом крутого восхождения. Алгоритм метода крутого восхождения заключается в проведении следующих операций. 1. Выбор базового фактора. Фактор, для которого произведение коэффициента регрессии на интервалах варьирования максимально, называют базовым: а = max (В∙Х). 2. Для базового фактора выбирают шаг крутого восхождения h, равный интервалу варьирования Ха. 3. Пересчитывают составляющие градиента по выбранному шагу крутого восхождения:
4. Округляют шаг крутого восхождения. 5. Организуют поиск оптимальной области путем последовательного прибавления составляющих градиента уравнения регрессии к нулевому уровню. Получают серию значений факторов крутого восхождения. Переводят факторы крутого восхождения в кодированную форму и получают расчетное значение переменной состояния Y. Через несколько шагов ставят эксперименты, проверяя соответствие расчета и эксперимента. Стратегия проведения опытов состоит в том, чтобы найти такие шаги, которые увеличивают выходную переменную, а затем ее уменьшают.
Пример. Получено уравнение регрессии следующего вида: Y = 23,28 + 1,78∙ X 1 + 10,23∙ X 2 + 9,36∙ X 3 Требуется осуществить поиск максимальных значений параметра Y. Результаты крутого восхождения приведены в табл.3.4. Таблица 3.4 Исходные данные и результаты крутого восхождения
В табл. 3.4 даны расчетные значения параметра и экспериментальной величины процесса (Y).
В качестве примера рассчитаем значение Y для опыта 9: Х 1 = 0,74: кодированное значение Х 1 = (0,74 – 0,7)/0,2 = 0,2; Х 2 = 140: кодированное значение Х 2 = (140 – 135)/5 = 1; Х 3 = 45: кодированное значение Х 3 = (45 – 30)/15 = 1 Y = 23,28 + 1,78∙0,2 + 0,23 + 9,36 = 43 Крутое восхождение в данном примере эффективно: в опыте 13 достигнуто максимальное значение параметра.
Исходные данные для выполнения работы
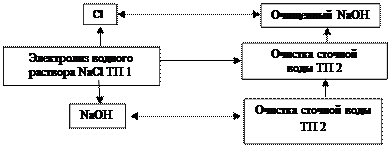
В работе необходимо построить математическую модель извлечения ртути из раствора при производстве хлора и щелочи электролизом хлорида натрия на ртутном катоде. В качестве переменной состояния выбирают показатель «содержание ртути на выходе процесса». Так как раствор электролита сбрасывают в водный бассейн, цель моделирования состоит в установлении таких параметров работы, при которых содержание ртути в растворе минимально. Технологическая схема получения хлора и щелочи изображена на рис.3.1.1. Процесс очистки раствора осуществляет методом экстракции. Экстракция зависит от скорости вращения мешалки, температуры раствора, времени пребывания раствора в реакторе. Нулевые уровни факторов: Х 10 = 2500 об/мин; Х 20 = 100 °С; Х 30 = 45 мин. Интервалы варьирования: Х 1 = 500 об/мин; Х 2 = 10 °С; Х 3 = 15 мин.
Рис. 3.1. Технологическая схема получения хлора и щелочи электролизом хлорида натрия на ртутном катоде
Порядок выполнения работы 1. Получить вариант выполнения работы (табл. 3.5). 2. В соответствии с матрицей планирования провести расчет коэффициентов линейного уравнения регрессии. 3. Оценить значимость коэффициентов регрессии. 4. Проверить адекватность уравнения. 5. Из уравнения регрессии найти условия процесса, которые обеспечивают минимальное содержание ртути в растворе. Таблица 3.5 Матрица планирования эксперимента
Продолжение табл. 3.5
Окончание табл. 3.5
Задания к выполнению графической части работы
Провести построение функции отклика Y от параметров X1, X2, X3: Y= f (X1, X2, X3).
Вопросы для подготовки теоретической части
1. Методы исследования поведения сложных систем. 2. Прогнозирование развития экологических систем. 3. Виды моделирования. Модели устойчивого развития экологических систем. 4. Основные положения планирования эксперимента.
Литература [1-4,19 -21, 24, 26, 29, 41].
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 100; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.147.12 (0.009 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

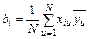 (i=1,2,…,n), (3.4)
(i=1,2,…,n), (3.4)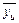 – среднее значение по параллельным опытам u -й строки матрицы планирования; х i – уровень фактора (+1, -1).
– среднее значение по параллельным опытам u -й строки матрицы планирования; х i – уровень фактора (+1, -1).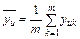 , (3.5)
, (3.5)
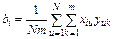 . (3.6)
. (3.6)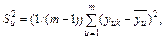 (3.7)
(3.7)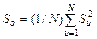 (3.8)
(3.8)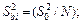 (3.9)
(3.9)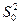 и числа строк матрицы планирования N;
и числа строк матрицы планирования N;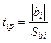 (3.10)
(3.10)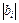 - абсолютное значение i-го коэффициента регрессии,
- абсолютное значение i-го коэффициента регрессии,  среднеквадратичное отклонение
среднеквадратичное отклонение 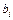
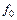 и уравнению значимости
и уравнению значимости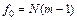 (3.11)
(3.11)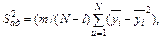 (3.13)
(3.13)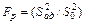
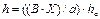 , (3.15)
, (3.15)