
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы статистической обработкирезультатов испытанийСодержание книги
Поиск на нашем сайте ГРУНТЫ Методы статистической обработкирезультатов испытаний
Предисловие Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0-92 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-2009 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, применения, обновления и отмены» Сведения о стандарте 1 РАЗРАБОТАН Научно-исследовательским, проектно-изыскательским и конструкторско-технологическим институтом оснований и подземных сооружений им. Н.М. Герсеванова (НИИОСП им. Н.М. Герсеванова), ОАО «НИЦ «Строительство» при участии Национального объединения изыскателей (НОИЗ), Московского геологоразведочного института (МГРИ - РГГРУ) 2 ВНЕСЕН Техническим комитетом по стандартизации ТК 465 «Строительство» 3 ПРИНЯТ Межгосударственной научно-технической комиссией по стандартизации, техническому нормированию и оценке соответствия в строительстве (приложение В к протоколу № 40 от 4 июня 2012 г.) За принятие проголосовали:
4 Приказом Федерального агентства по техническому регулированию и метрологии от 29 октября 2012 г. № 597-ст межгосударственный стандарт ГОСТ 20522-2012 введен в действие в качестве национального стандарта Российской Федерации с 01 июля 2013 г. 5 ВЗАМЕН ГОСТ 20522-96 Информация о введении в действие (прекращении действия) настоящего стандарта публикуется в ежемесячно издаваемом указателе «Национальные стандарты». Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра или отмены настоящего стандарта соответствующая информация будет опубликована в ежемесячно издаваемом информационном указателе «Национальные стандарты» Содержание
ГОСТ 20522-2012 МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ ГРУНТЫ Методы статистической обработки результатов испытаний Soils. Methods of statistical treatment of test results Дата введения - 2013-07-01 Область применения Настоящий стандарт устанавливает применяемые при инженерно-геологических изысканиях, проектировании и строительстве методы статистической обработки результатов испытаний грунтов, составляющих различные грунтовые объекты (основания сооружений, массивы, вмещающие подземные сооружения, сооружения из грунта, склоны и т.д.). Данные методы применяют для статистической обработки результатов определений физических и механических (прочностных и деформационных) характеристик всех грунтов (см. ГОСТ 25100), а также для выделения инженерно-геологических и расчетных грунтовых элементов. Требования настоящего стандарта не распространяются на параметры прочности и деформируемости грунтов при динамических воздействиях, а также на характеристики крупнообломочных грунтов, получаемые с применением моделирования гранулометрических составов. Нормативные ссылки В настоящем стандарте использованы ссылки на следующие межгосударственные стандарты: ГОСТ 12248-2010 Грунты. Методы лабораторного определения характеристик прочности и деформируемости ГОСТ 25100-2011 Грунты. Классификация Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов на территории государства по соответствующему указателю «Национальные стандарты», составленному на 1 января текущего года, и по соответствующим информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку. 3 Термины и определения В настоящем стандарте применены следующие термины с соответствующими определениями: 3.1 вероятность: Числовая характеристика возможности появления какого-либо определенного события в тех или иных определенных условиях, которые могут повторяться неограниченное число раз, выражаемая в долях единицы или процентах. Вероятности, с которыми характеристики грунтов, трактуемые как случайные величины, принимают те или иные значения, образуют распределение вероятностей, для установления которого по выборочным данным оценивают один или несколько параметров распределения. 3.2 доверительный интервал: Интервал, вычисленный по выборочным данным, который с заданной вероятностью (доверительной) накрывает неизвестное истинное значение оцениваемого параметра распределения. 3.3 доверительная вероятность: Вероятность того, что доверительный интервал накроет неизвестное истинное значение параметра, оцениваемого по выборочным данным. 3.4 односторонняя доверительная вероятность: Вероятность того, что неизвестное истинное значение параметра не выйдет за пределы нижней (или верхней) границы доверительного интервала. 3.5 среднее значение (выборочное): Среднеарифметическое частных значений, образующих выборку величин, независимых друг от друга и от пространственных координат. 3.6 среднеквадратическое отклонение: Мера отклонения опытных данных от выборочного среднего значения или функциональной зависимости, выражаемая в абсолютных единицах и вычисляемая по формулам (4), (12). 3.7 коэффициент вариации: Мера отклонения опытных данных от выборочного среднего значения, выражаемая в долях единицы или процентах и вычисляемая по формуле (5). 3.8 сравнительный коэффициент вариации: Мера изменчивости величины, зависящая от начала отсчета выборки и вычисляемая по формуле (А.1) приложения А. 3.9 число степеней свободы: Число независимых наблюдений, равное числу определений n характеристики минус число оцениваемых статистических параметров. 3.10 метод наименьших квадратов: Метод статистической оценки функциональной зависимости путем установления таких ее параметров, при которых сумма квадратов отклонений опытных данных от этой зависимости является минимальной. 3.11 инженерно-геологический элемент; ИГЭ: Основная грунтовая единица при инженерно-геологической схематизации грунтового объекта, определяемая положениями 4.6. 3.12 расчетный грунтовый элемент; РГЭ: Основная грунтовая единица, выделяемая с учетом применяемого при проектировании грунтового объекта расчетного или экспериментального метода, определяемая по 4.6. Общие положения 4.1 Статистическую обработку результатов испытаний проводят для оценки неоднородности грунтов, выделения ИГЭ, а при необходимости и РГЭ, и вычисления нормативных и расчетных значений характеристик грунтов. 4.2 Опытные данные, для которых проводится статистическая обработка, должны быть получены единым методом испытания. 4.3 Применяемые в настоящем стандарте методы статистической обработки используют нормальный закон распределения вероятностей. При обосновании могут быть использованы и другие законы распределения, например, логарифмически нормальный (см. приложение Б). 4.4 Неоднородность грунта оценивают с помощью коэффициента вариации характеристик грунта (см. 6.4). Для сравнения неоднородности по разным характеристикам может применяться сравнительный коэффициент вариации (см. приложение A). 4.5 Статистическую обработку проводят для частных значений характеристик грунтов или фиксируемых в отдельных испытаниях величин, которые составляют случайную выборку. При наличии закономерного изменения характеристики в каком-либо направлении (чаще всего с глубиной) статистическую обработку проводят для определения параметров корреляционной зависимости, аппроксимирующей опытные точки линейной или кусочно-линейной функцией. 4.6 Статистическую обработку результатов испытаний выполняют для ИГЭ или РГЭ. За ИГЭ принимают некоторый объем грунта одного и того же происхождения, подвида или разновидности (см. ГОСТ 25100) при условии, что значения характеристик грунта изменяются в пределах элемента случайно (незакономерно) либо наблюдающаяся закономерность такова, что ею можно пренебречь. В случае выявления закономерности должны выполняться требования 5.5. ИГЭ наделяют постоянными нормативными и расчетными значениями характеристик. Комплекс ИГЭ используют при создании инженерно-геологической модели объекта. За РГЭ принимают некоторый объем грунта не обязательно одного и того же происхождения, подвида или разновидности, в пределах которого нормативные и расчетные значения характеристик по условиям применяемого расчетного или экспериментального метода проектирования объекта могут быть постоянными или закономерно изменяющимися по направлению (чаще всего по глубине). РГЭ может включать в себя один или несколько ИГЭ. Комплекс РГЭ используют при создании расчетной геомеханической модели объекта. Примечания 1 Местоположение, конфигурацию и объем ИГЭ и РГЭ устанавливают с учетом сведений об объекте строительства и геологических данных. 2 Выделение РГЭ должно осуществляться совместно изыскателем и проектировщиком. 4.7 Для всех характеристик грунта вычисляют нормативные, а для характеристик, используемых в расчетах, и расчетные значения. Нормативные значения характеристик определяют как среднестатистические, получаемые осреднением их частных значений, или отвечающие осредненным по частным значениям аппроксимирующим зависимостям между измеряемыми в опытах величинами (или функционально с ними связанными величинами), или по зависимостям каких-либо из этих величин от координат по одному из направлений. Расчетное значение получают делением нормативного значения на коэффициент надежности по грунту γ g. 4.8 Коэффициент надежности по грунту γ g должен устанавливаться с учетом изменчивости и числа определений характеристики (числа испытаний) при заданной доверительной вероятности. Примечания 1 В расчетное значение характеристики проектировщиком в соответствии с указаниями норм проектирования различных видов сооружений могут вводиться и другие коэффициенты надежности, учитывающие влияние факторов, которые не могут быть учтены статистическим путем. 2 Для отдельных характеристик грунтов по указаниям норм проектирования различных видов сооружений их расчетные значения могут быть приняты равными нормативным значениям. 4.9 Значения доверительной вероятности при вычислении расчетного значения характеристики грунта принимают в соответствии с рекомендациями норм проектирования различных видов сооружений и должны быть указаны в техническом задании и программе работ на проведение инженерно-геологических изысканий. 4.10 Число определений характеристики грунтов, необходимое для вычисления ее нормативного и расчетного значения, может быть установлено из формулы (6) в зависимости от заданных коэффициента вариации характеристики, показателя точности (погрешности) ее среднего значения и доверительной вероятности. Минимальное число определений характеристик грунтов или фиксируемых в опытах значений должно быть шесть. Примечания 1 Число определений частных значений tg φ j и cj в первом способе и число определений пар τ i и σ i во втором способе должно быть не менее шести. 2 Методика статистической обработки результатов испытаний грунтов при трехосном сжатии приведена в приложении Д. 7.2 При статистической обработке частных значений tg φ j и cj для каждой j -й точки отбора монолита грунта в пределах ИГЭ предварительно вычисляют по методу наименьших квадратов указанные частные значения по результатам не менее трех определений сопротивления грунта срезу τ i при трех последовательных значениях нормального напряжения σ i (см. ГОСТ 12248):
где k - число определений τв каждой точке ИГЭ. Если при вычислении по формуле (10) получается значение с j < 0, то принимают значение с j = 0, а tg φ j вычисляют по формуле
7.3 По найденным частным значениям tg φ j и cj вычисляют нормативные значения tg φ n и сn по формуле (2) и среднеквадратические отклонения s tg φи S с по формуле (4). 7.4 Проводят статистическую проверку для исключения возможных ошибок в значениях tg φ j и cj в соответствии с 6.3. Пару значений tg φ j и cj исключают, если хотя бы для одного из них выполняется условие (3). При этом для оставшихся опытных данных следует заново вычислить значения tg φ n, с n, S tg φи Sc. 7.5 Вычисляют для tg φи с коэффициент вариации V, показатель точности ρα, коэффициент надежности по грунту γgи их расчетные значения по формулам (5)-(8). Примечание - Если по формуле (6) для tg φили с получится значение ρα> 1, то расчетное значение этой характеристики следует принять равным нулю. 7.6 При статистической обработке всех n пар опытных значений τ i и σ i как единой совокупности нормативные значения tg φ n, с n вычисляют по формулам (9) и (10), в которых значения tg φ j, с j и k необходимо заменить на tg φ n, с n и n соответственно. Если при этом получится значение сn < 0, то принимают сn = 0, а tg φ n вычисляют вновь по формуле (11), в которой необходимо заменить tg φ j и k на tg φ n и n соответственно. Примечание - При существенной нелинейности зависимости τ= f (σ)ее аппроксимируют кусочно-линейной зависимостью и выполняют статистическую обработку для каждого линейного участка отдельно, при этом число пар опытных значений σ i и τ i на каждом линейном участке должно быть не менее шести. 7.7 Вычисляют среднеквадратическое отклонение сопротивления срезу S τпо формуле
Примечание - В формуле (12) следует заменить n - 2 на n - 1, если в соответствии с 7.6 принято сn = 0, а tg φ n вычислен по формуле (11). 7.8 Выполняют статистическую проверку для исключения возможных ошибок в значениях τ i в соответствии с 6.3. Исключают наиболее отклоняющееся от нормативной зависимости τ n = сn + σtg φ n значение τ i, для которого выполняется условие (3). При этом в условие (3) следует подставить вместо Хi проверяемое значение τ i, вместо Хn - соответствующее τ i значение τ n и вместо S - значение S τиз формулы (12). Если какое-либо значение τ i будет исключено, следует заново вычислить значения tg φ n, сn и S τпо оставшимся опытным данным. 7.9 Расчетные значения tg φи с вычисляют с учетом заданного диапазона нормальных напряжений σmin, σmax, который принимают в соответствии с программой работ. При отсутствии таких указаний следует принимать σmin и σmax равными минимальному и максимальному нормальным напряжениям, имевшим место при испытании грунта на срез. Вычисляемые значения tg φи с должны сопровождаться сведениями о принятом диапазоне нормальных напряжений. 7.10 Вычисляют нормативные значения сопротивления грунта срезу τ ' n и τ '' n и значения полудлин совместных доверительных интервалов δ ' τи δ '' n при значениях нормального напряжения σ= σmin и σ= σmax по формулам (13) и (14):
где V α,λ- коэффициент, принимаемый по таблице Е.3 или Е.4 приложения Е в зависимости от заданной односторонней доверительной вероятности α, параметра λ, вычисляемого по формуле (16), и числа степеней свободы К = n - 2;
σ i - опытные значения нормального напряжения. 7.11 Параметр λ, учитывающий значения диапазона /σmin, σmax/, вычисляют по формуле
где
7.12 Вычисляют расчетные значения сопротивления срезу τ ' и τ '' при нормальных напряжениях σ= σmin и σ= σmax и коэффициенты надежности по грунту γ g , tg φ и γ g , c для tg φи c по формулам (19) и (20):
Расчетные значения tg φи с вычисляют по формуле (8). Если
Приложение А Статистические таблицы Таблица Е.1 - Значения критерия v при двусторонней доверительной вероятности α = 0,95
Таблица Е.2 - Значения коэффициента t α
Таблица Е.3 - Значения коэффициента V α (α = 0,85)
Таблица Е.4 - Значения коэффициента V α (α = 0,95)
Таблица Е.5 - Значения критерия F α при доверительной вероятности α = 0,95
Ключевые слова: грунты, статистическая обработка результатов испытаний, инженерно-геологический элемент, нормативное значение характеристики, расчетное значение характеристики
ГРУНТЫ Методы статистической обработкирезультатов испытаний
Предисловие Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0-92 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-2009 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, применения, обновления и отмены» Сведения о стандарте 1 РАЗРАБОТАН Научно-исследовательским, проектно-изыскательским и конструкторско-технологическим институтом оснований и подземных сооружений им. Н.М. Герсеванова (НИИ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


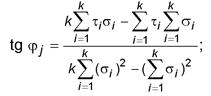 (9)
(9)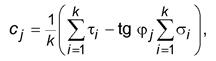 (10)
(10)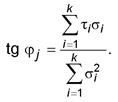 (11)
(11)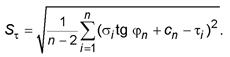 (12)
(12)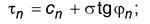 (13)
(13)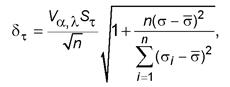 (14)
(14)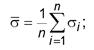 (15)
(15)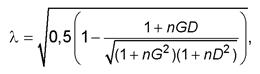 (16)
(16)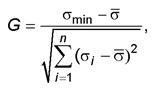 (17)
(17)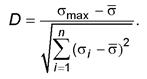 (18)
(18)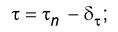 (19)
(19)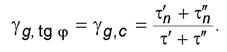 (20)
(20)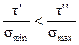 , то вместо формулы (20) следует использовать формулу (21):
, то вместо формулы (20) следует использовать формулу (21):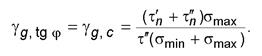 (21)
(21)


