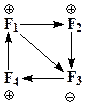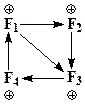Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование технологических процессовСодержание книги
Поиск на нашем сайте
И экологических систем В изучении природных и технологических процессов следует выделить два основных метода исследования, таких, как мониторинг и моделирование. В предыдущих главах показано, что мониторинг как элемент экспертизы состоит из наблюдения за природой, анализа состояния окружающей среды, контроля за выбросами вредных веществ, рекомендаций по улучшению экологической обстановки, приведения в действие нормативных и законодательных актов, регулирующих хозяйственную деятельность субъектов. Мониторинг допускает моделирование процессов, но в узкой трактовке рассмотрим мониторинг как метод наблюдения за природой, выделив моделирование в отдельную область исследования. Моделированием называют получение модели, дающей информацию об исследуемом процессе или явлении. Модель – это система, отражающая отдельные стороны явления, процесса. Существуют несколько видов моделирования: имитационное, или аналоговое; физическое; математическое; комбинированное. В системном анализе применяют такие термины, как входной эффект и выходной эффект; под выходом понимается любое воздействие на систему со стороны окружающей или внешней среды или соседней системы. В качестве входного эффекта может рассматриваться любой вид техногенного воздействия на геологическую среду или их комплекс. И наоборот, соответствующими выходными эффектами, или выходами, называются изменения (или отклики), которые претерпевает система. Входные эффекты представляют собой внешние факторы по отношению к рассматриваемой системе (техногенная компонента), а выходные эффекты могут быть изменениями ее свойств и характеризоваться комплексом параметров. В системном анализе выделяют четыре типа моделей: 1) модель типа «черный ящик»; 2) модель состава; 3) модель структуры; 4) комплексная модель (сочетание первых трех) (рис. 6.1).
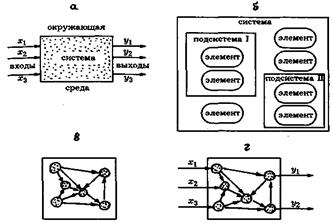
Рис. 4.1. Типы статических моделей систем: а – модель «черного ящика»; б – модель состава; в – модель структуры; г – структурная схема модели системы Модель «черного ящика». Когда ничего неизвестно о внутреннем составе и устройстве самой исследуемой системы, то ее модель можно представить в виде «ящика», выделенного из окружающей среды, так называемого «черного ящика». Связи со средой осуществляют «входы» и «выходы» рассматриваемой системы (рис. 6.1, а).
Модель «черного ящика» используется и на начальных этапах исследований, на начальных стадиях организации мониторинга. Цель использования модели «черного ящика» проста: варьируя входными переменными интенсивностью техногенных воздействий (или исследуя их в разных условиях), исследователь изучает реакцию на них выходных параметров изменений окружающей среды или ее элементов. Анализируя затем эту реакцию на выходе, можно сделать ряд важных практических выводов о самой системе. При использовании этой модели в системе мониторинга она реализуется на ЭВМ, и поставленные задачи решаются подбором до наилучшего совпадения входных и выходных параметров. На основе анализа входных и выходных параметров устанавливают детальные модели состава и структуры. Модель состава системы. Модель состава окружающей среды (ее элементов) может рассматриваться в широком и узком смысле. В широком смысле подсистемами окружающей среды являются почвы, воды, рельеф, воздух, процессы и явления (рис. 6.1, б). В каждой из этих подсистем могут быть выделены свои подсистемы и так далее до элементов. Модель структуры системы. Совокупность необходимых и достаточных для достижения цели отношений между элементами называется структурой системы. Перечень связей между отдельными (или всеми) элементами системы и ее подсистемами (т.е. структура системы) является отвлеченной, абстрактной моделью: в ней установлены только отношения между элементами, но не рассмотрены сами элементы. На практике же установлению связей и отношений между элементами окружающей среды всегда предшествует построение модели состава, т.е. выделение перечня элементов. Графически модель структуры выражается в виде набора связей разного типа между элементами (рис. 6.1, в). Комплексная модель системы. Объединяя в одну модель «черный ящик», модель состава и структуры системы, мы получим в итоге комплексную модель окружающей среды (ее части), или «структурную схему системы» (или «белый ящик», «прозрачный ящик»). В структурной схеме (не путать со структурной моделью) указываются все элементы системы, все связи между элементами внутри системы и связи определенных элементов с окружающей внешней средой (т.е. входы и выходы системы). Графически структурная схема системы содержит в себе все элементы ее составных моделей (рис. 6.1, г).
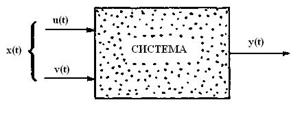
Все структурные схемы имеют нечто общее, что побудило математиков рассматривать их как особый объект математических исследований. Получилась схема, в которой обозначается только наличие элементов и связей между ними, а также (в случае необходимости) разница между элементами и между связями. Такая схема называется графом, а соответствующий раздел математики – теорией графов. В теории графов предусмотрены и разработаны и различные операции преобразования графов, определения их вероятностных характеристик (вероятностные, или стохастические, графы). Графы могут изображать любые структуры, если не накладывать ограничений на пересекаемость ребер. Системы, в которых происходят какие-либо изменения во времени, называются динамическими, а модели, их отражающие, – динамическими моделями систем. Реальные природно-технические системы, реальные объекты геологической среды представляют собой динамические системы, изменяющиеся во времени. Развитие динамических моделей происходит примерно в той же последовательности, как это излагалось: от «черного ящика» к «белому» (рис. 6.2). На этапе создания модели «черного ящика» различают два типа динамики системы: ее функционирование и развитие. Под функционированием понимают те процессы, которые происходят в системе (и окружающей ее среде), стабильно реализующей фиксированную цель. Развитием же называют то, что происходит с системой при изменении ее целей. Развитие ПТС осуществляется человеком при модернизации производства, смене технологий на более совершенные и т.п. Следующий шаг в построении динамических моделей систем состоит в том, чтобы конкретнее отобразить происходящие в них изменения, в частности техногенные изменения геологической среды. Типы динамических моделей такие же, как и статических, только элементы этих моделей имеют временной характер. Для динамической модели структуры необходимо установить последовательность действий и продолжительность каждого действия между связями и отношениями.
Рис. 4.2. Динамическая модель «черного ящика»
Все указанные выше типы моделей систем являются формальными, относящимися к любым системам окружающей среды. Чтобы получить модель заданной системы, нужно придать формальной модели конкретное содержание, т.е. решить, какие аспекты реальной системы включить в элементы модели избранного типа, а какие – нет, считая их несущественными. Процесс построения содержательных моделей окружающей среды или ее элементов является процессом творческим, интеллектуальным. Формальная модель является «окном», через которое исследователь смотрит на реальную систему, строя содержательную модель окружающей среды. Имитационное или аналоговое моделирование используют в биологии, биохимии при изучении отдельных компонентов экологических систем. Простейший пример аналогового моделирования – изучение развития замкнутой экологической системы в процессе брожения гексоз под действием микроорганизмов – дрожжей Sacchoromyces и перенос полученных закономерностей на другие системы.
Как установлено, спиртовое брожение может быть выражено следующим уравнением:
C6H12O6 = 2CO2 + 2С2H5OH + ΔH
Здесь ΔH – тепловой эффект химического процесса, Дж/моль. Доказано, что спиртовое брожение происходит под действием биологических катализаторов – ферментов и имеет ряд промежуточных стадий. На первой стадии образуется гексозодифосфат, который превращается в фосфат глицеринового альдегида и фосфат диоксиацетона. На второй стадии фосфат глицеринового альдегида окисляется с образованием фосфоглицериновой кислоты. Из фосфоглицериновой кислоты синтезируется пировиноградная кислота, которая распадается на ацетальдегид и оксид углерода. На последней стадии ацетальдегид восстанавливается до спирта. Ферментная система, вызывающая брожение, состоит из нескольких биологических катализаторов, важнейшими из которых являются дегидраза, карбоксилаза. Так, гексозодифосфат преобразуется под действием фермента «альдолазы». Фосфат глицеринового альдегида и фосфат диоксиацетона изомеризуются под влиянием фосфотриазоизомеразы. Окисление фосфата глицеринового альдегида происходит под действием фермента козимазы. Енолаза катализирует процессы, связанные с синтезом пировиноградной кислоты. Карбоксилаза превращает пировиноградную кислоту в ацетальдегид из которого под действием дигидрокозимазы образуется этиловый спирт. Предложенная схема брожения объясняет образование эквимолярных количеств спирта и оксида углерода (IV), а также постоянное наличие в системе небольших количеств глицерина и ацетальдегида. Основные продукты жизнедеятельности дрожжей – углекислый газ, этиловый спирт, теплота химической реакции приводят к повышению температуры и загрязнению системы. Через некоторое время концентрация спирта в системе достигает 10–14%, как следствие, происходит гибель микроорганизмов, т.е. развитие является неустойчивым (рис.3.3). Выделим следующие стадии развития системы: устойчивый рост, равновесие, гибель системы. Характерно, что человеческая цивилизация развивается по принципам жизнедеятельности примитивных микроорганизмов в замкнутой системе. Отметим, что к концу XX в. цивилизация вступила в область равновесия, за которым следует гибель при отсутствии каких-либо кардинальных мероприятий по охране окружающей среды. При физическом моделировании проводят воспроизведение процесса в различных масштабах. Исследование развития микроорганизмов при спиртовом брожении в пробирке и перенос полученных закономерностей на технологию получения спирта в промышленном масштабе – результат физического моделирования. В аналоговом моделировании мы перенесли результаты исследования одной системы на совершенно другую и более сложную систему.
При математическом моделировании изучение явления осуществляется на математической модели – уравнении, системе уравнений, описывающих всю совокупность процесса:
где X, Y, Z, t, n – факторы или параметры процесса; f 1, f 2,..., f п – функции, связывающие параметры в уравнении. Особенность математического моделирования состоит в варьировании условий функционирования процесса путем параметрического изменения факторов, что сокращает время проведения анализа модели. Математическое моделирование сочетается с другими видами моделей, поэтому наиболее часто применяют комбинированные модели. Рассмотрим пример комбинированного моделирования – очистку раствора каустической соды от ртути. Получим линейное уравнение, описывающее данный процесс. Эксперименты по очистке каустической соды проводили в лабораторном реакторе, имеющем термостат. Из реактора ртуть экстрагировали специальными органическими веществами. Алгоритм моделирования: 1. Выбор факторов, влияющих на содержание ртути: X 1 – скорость вращения мешалки, об/мин; X 2 – температура раствора,ºС; X 3 – время экстракции ртути, мин. 2. Составление матрицы планирования эксперимента (табл.4.1).
Таблица 4.1 Матрица планирования эксперимента по очистке Каустической соды от ртути
Значения +1, –1 называют уровнями факторов, которые фиксируют при проведении эксперимента. Уровни факторов – это кодированные значения параметров процесса:
где X i0 – нулевые уровни; Δ X i – интервал факторов. X 10 =2500 об/мин; X 20 =100 ºС; X 30 =40 мин; Δ X 1 =500 об/мин; Δ X 2 = 10 ºС; Δ X 3 = 15 мин. Уровни факторов выбирают по имеющейся априорной информации о процессе. 3. Расчет коэффициентов математической модели проводят по формуле
где y i – среднее значение содержания ртути в каустической соде в опытах. Необходимо обратить внимание, что значения уровней факторов выбирают для каждой строки табл. 3.1 в кодированной форме: +1, –1:
b 0 =10–4(0,90+1,14 + 2,86+3,22+2,70+2,80+3,54+6,45)/8 =2,95∙10–4; b 1 = 10–4(0,90+1,14 – 2,86+3,22-2,70+2,80–3,54 +6,45)/8 =0,45∙10–4; b 2 = 10–4(0,90+1,14 – 2,86–3,22+2,70+2,80–3,54–6,45)/8 =– 1,07∙10–4; b 3 = 10–4(0,90+1,14+2,86+3,22–2,70–2,80–3,54–6,45)/8 =0,92∙10–4.
4. Составление математического уравнения
Y = b 0 + b 1 X 1 + b 3 X 3, Y =10–4 (2,95 + 0,45 X 1 – 1,07 X 2 + 0,92∙ X 3),
где Y – содержание ртути в каустической соде, %. Получив уравнение или математическую модель, проводят анализ: – рассчитывают ошибку опыта; – проверяют значимость коэффициентов b i; – проверяют адекватность уравнения или его точность;
– определяют оптимальные условия, при которых содержание ртути в растворе минимально; – принимают решение по охране окружающей среды от выбросов ртути. Рассмотренный вид моделирования относится к разновидности регрессионного анализа или полного факторного эксперимента (ПФЭ), устанавливающего зависимость между числом факторов N и количеством опытов, необходимых для построения уравнения регрессии. Специальные методы комбинированного моделирования природных процессов, содержащие элементы запаздывания причинно-следственных связей, разработаны в 70-х гг. XX в. группой исследователей под руководством Д. Медоуза. Основной принцип моделирования основан на изучении поведения существенного фактора системы в зависимости от набора параметров, влияющих на природные процессы. Поведение существенного фактора представляется в виде уравнения, диаграммы или базовой динамики. Диаграмма, график, уравнение позволяют провести системный анализ проблемы и установить причинные связи между явлениями. Формализованная запись существования причинных связей отображается схемой:
F1 ──> F2
Схема означает, что с изменением F1 меняется величина F2. Существуют два типа причинных воздействий – положительные и отрицательные:
F1──> ±F2.
В реальных системах структура связей между явлениями гораздо сложнее, чем схемы, изображенные формализованной записью. Для того чтобы показать совокупность взаимодействующих процессов, цепочки причинных связей, изображенные формализованной записью, замыкают в контуры – кольца обратных связей. Предположим, исследуют систему F2. В системе F2 произошло возрастание одного параметра, который вывел ее из равновесия. Двигаясь по внешнему контуру, заметим, что системы F3, F4, F1, уменьшились. Через некоторое время (время запаздывания) система F2 вернется в первоначальное положение. Следовательно, система F1 становится собственной причиной своего поведения во времени, а гомеостаз системы F2 обусловлен наличием отрицательного кольца обратной связи. Гомеостаз системы – удержание величины F2 на некотором уровне или ее способность сопротивляться внешним воздействиям – обусловлен наличием отрицательного кольца обратной связи. В моделировании необходимо находить действующую отрицательную обратную связь, которая сопротивляется внешним воздействиям, способствуя сохранению окружающей среды. Существуют системы, в которых существенный фактор постоянно увеличивается по определенному закону (рис.4.3). Развитие таких систем неустойчиво, они разрушаются с течением времени, не выдерживая нагрузки. В рамках формального представления явлений в виде цепочки причинных связей подобный случай реализуется в цепи F1, F2, F3, F4 с положительным контуром обратной связи.
а б
Рис. 4.3. Примеры устойчивого (а) и неустойчивого развития систем (б)
Все процессы, происходящие в природе, можно представить в виде колец обратных связей с различным смысловым наполнением факторов, влияющих на развитие системы, но необходимо различать желаемое, воспринимаемое, действительное состояния системы. Между желаемым, воспринимаемым и реальным состояниями существуют различия. Предположим, необходимо довести наблюдаемое состояние до определенного уровня F1. Для достижения этого уровня предпринято воздействие на систему. В зависимости от условия воздействия состояние системы снизится на более низкий уровень или приблизится к желаемому уровню F1. Наблюдаемое состояние F2 может не отражать реальных процессов, протекающих в системе. Сформулируем наиболее общие положения, позволяющие привести реальное состояние к желаемому: – воздействовать на систему необходимо путем изменения структуры, отвечающей за нежелательную динамику развития; – постоянное усиление действия одних и тех же параметров приводит к неустойчивому развитию и гибели системы; – поддерживать нормативы, стандарты, не допуская выхода процессов из равновесия; – снизить запаздывание при переходе от действия к реальному и воспринимаемому состоянию; – добавить действие противоположного типа (контур с отрицательной связью); – использовать такие методы анализа и наблюдения, которые дают небольшие отклонения реального состояния от воспринимаемого. Применение общих принципов экологической экспертизы к развитию биосферы позволили построить различные модели развития человеческого общества. Экспериментальной основой послужили статистические данные производства продуктов потребления, роста населения, загрязнения окружающей среды. Модель с неустойчивым развитием по сценарию жизни примитивных микроорганизмов рассмотрена ранее на примере брожения гексоз под действием дрожжей. Поясним этот процесс подробнее. Производство продуктов питания, объем промышленного производства, численность народонаселения возрастает до тех пор, пока истощение ресурсов не приведет к замедлению развития производства. Наличие запаздывания в системе причинно-следственных связей производства: рост населения, загрязнение окружающей среды – приведет к гибели системы из-за загрязнения окружающй среды и нехватки продуктов питания. Можно предположить, что при неисчерпанных природных и энергетических ресурсах модель предскажет устойчивое развитие. В действительности моделирование показало, что при неисчерпаемых природных и энергетических ресурсах коллапс и гибель системы наступит к 2100 г. Модель предсказывает устойчивое развитие человеческого общества при определенных ограничениях параметров экологической системы: – ограничение роста производства, перераспределение материальных благ в сторону менее развитых стран; – контроль над рождаемостью; – комплексное использование вторичных ресурсов, возврат в производство отходов не менее чем на 80%; – рациональное использование энергетических ресурсов, установление пределов максимального потребления энергии. Важность комплексного регулирования перечисленных выше параметров иллюстрируется следующим примером. Допустим, нам удалось возвращать в производство 75% вторичных материалов, но рост производства неограничен. Урожайность сельскохозяйственных культур удвоили, осуществили контроль за уровнем рождаемости. Гибель цивилизации в данном случае неизбежна из-за истощения природных ресурсов и загрязнения окружающей среды.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.124.212 (0.015 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

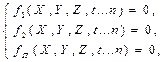
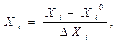
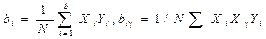 ,
,