Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоемкость идеальных газов и их смесейСодержание книги
Поиск на нашем сайте Под теплоемкостью рабочего тела в некотором процессе понимают количество тепла, которое необходимо подвести или отвести для того, чтобы изменить его температуру на 1 К:
Теплоемкость единицы количества вещества называют удельной теплоемкостью. Различают удельные массовую
Между ними существует однозначная связь
Теплоемкость газа зависит от характера процесса подвода теплоты и параметров. В зависимости от процесса теплоемкость любого газа может изменяться от Теплоемкость газов зависит (в общем случае) от параметров Согласно молекулярно-кинетической теории газа изобарные и изохорные теплоемкости не зависят от параметров, а зависят только от природы газа, от его атомности.
Между изохорной, изобарной теплоемкостями и показателем адиабаты существует однозначная связь.
Уравнение Майера
Для реальных газов теплоемкость сильно зависит от физической природы и параметров, прежде всего от температуры, с ростом температуры теплоемкость чаще всего увеличивается, показатель адиабаты уменьшается. Найдем, чему равны теплоемкость и показатель адиабаты смеси газов. Пусть имеем смесь, состоящую из n компонент:
…
Теплота, переданная смеси, равна сумме теплот, переданных компонентам этой смеси, при этом каждая компонента нагревается на одну и ту же температуру ΔТ:
Поделив правую и левую части этого выражения на произведение МсмΔТ получаем:
Аналогично для удельных мольных теплоемкостей
Таким образом, показатель адиабаты для смеси газов определяется следующим образом:
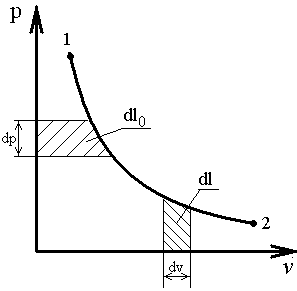
Работа объемной деформации «L» – работа, совершаемая вследствие деформации контрольной поверхности термодинамической системы. Элементарное количество работы объемной деформации
где
В термодинамике широко используется метод представления процессов в системе координат В ходе конечного процесса изменение давления зависит от его характера, поэтому для всего процесса
знак
Работа как форма обмена энергией обладает следующими свойствами: 1) работа– это функция процесса, количество работы в процессе зависит от пути перехода из одного состояния в другое; 2) 3) так как При термодинамическом анализе термодинамической системы со многими степенями свободы необходимо учитывать и другие виды работы, например механическую работу на валу, электрическую работу переноса электрического заряда в цепи, магнитная работа намагничивания магнитика в магнитном поле и др. Для работы объемной деформации давление является потенциалом взаимодействия, а перемещение – координатой взаимодействия. Располагаемая (полезная) работа «L 0»– это работа, которая может быть получена за счет падения давления
Располагаемая работа численно равна площади фигуры между кривой данного конечного процесса и осью давлений на рабочей (p-v) диаграмме.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

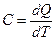 ,
, 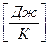
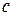 и мольную теплоемкости
и мольную теплоемкости 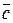 :
:
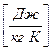 ;
; 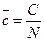
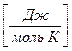 .
.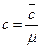 .
.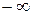 до
до 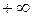 . В термодинамике широко используется понятия изобарной и изохорной теплоемкостей (
. В термодинамике широко используется понятия изобарной и изохорной теплоемкостей (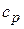 ,
, 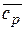 и
и 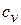 ,
, 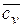 ) и их отношение
) и их отношение 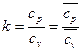 – показатель адиабаты.
– показатель адиабаты.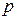 и
и 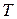 .
.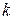
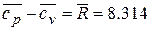
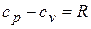
 ,
, 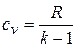 ,
, 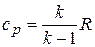
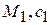 ;
; 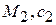 …
… 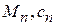 . Вся смесь нагревается в некотором диапазоне температур ΔТ. Тогда для каждой компоненты можно записать:
. Вся смесь нагревается в некотором диапазоне температур ΔТ. Тогда для каждой компоненты можно записать: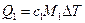
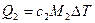
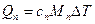
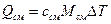
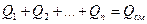
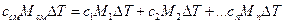
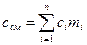
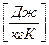
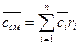
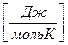
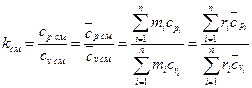
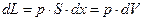
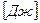
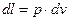
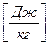
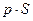 – сила;
– сила;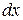 – перемещение.
– перемещение.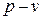 , называемый рабочей диаграммой, так как любая площадка на ней численно равна работе. Площадь фигуры между кривой процесса и осью удельных объемов численно равна работе объемной деформации этого процесса.
, называемый рабочей диаграммой, так как любая площадка на ней численно равна работе. Площадь фигуры между кривой процесса и осью удельных объемов численно равна работе объемной деформации этого процесса.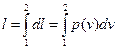
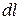 определяется знаком
определяется знаком 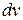
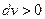 ,
, 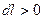 ,
, 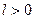 - работа объемного расширения;
- работа объемного расширения;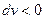 ,
, 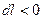 ,
, 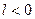 - работа сжатия.
- работа сжатия. , следовательно при круговом процессе (цикле) система получает от ОС (или отдает ей) некоторое количество энергии.
, следовательно при круговом процессе (цикле) система получает от ОС (или отдает ей) некоторое количество энергии.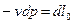 ,
,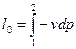 ,
,