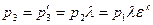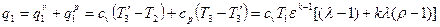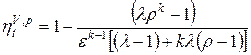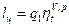Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет термодинамики. Основные черты термодинамического метода исследованияСодержание книги
Поиск на нашем сайте
Введение Памятка студенту. 1. Итоговый контроль знаний студентов предусматривает в разных группах либо экзамен, либо зачет. К итоговому контролю допускаются только те студенты, которые успешно выполнили программу практической части курса (выполнение и защита всех 4-х лабораторных работ). Студенты, не имеющие зачетной книжки на руках, к итоговому контролю не допускаются. 2. Студенты, имеющие академическую задолженность, и выполнившие требования по п.1, допускаются к переэкзаменовке только при наличии направления, либо ведомости из деканата. В запущенных случаях (третья переэкзаменовка или академическая задолженность сроком более чем 1 семестр) итоговый контроль проводится специальной комиссией из числа преподавателей каф. А8 в конце сессии, в назначенные для этого день и время. 3. Задача курса «Термодинамика» - в первую очередь научить студента методам термодинамического анализа. Это означает, что просто запомнить уравнения и определения мало. На итоговом контроле требуется показать, как и на основании чего они были получены, и какие выводы из них следуют. 4. Студент должен владеть базовыми понятиями термодинамики (см. приложение), на которых основаны общая термодинамика и термодинамический анализ тепловых машин. Незнание любого из этих понятий приравнивается к полному незнанию дисциплины. 5. В случае, если ведущим преподавателем (лектором) предусмотрен т.н «зачет/экзамен автоматом», его условия озвучиваются на первой или второй лекции. Эти условия определяются в первую очередь успешным выполнением студентом учебной программы практической части дисциплины к определенной дате. Зачет/экзамен автоматом проставляется лектором по рекомендации преподавателя, ведущего практическую часть курса. В случае несоответствия знаний студента пп.3 и 4 данной памятки, этот студент теряет право на зачет/экзамен автоматом. Приложение. Базовые понятия термодинамики (От студента требуется знание как определения указанного понятия, его размерности – если она есть, – так и математического выражения – если оно есть) 1. Понятия теплоемкости, ТДС, основных термодинамических параметров (р, v, Т), внутренней энергии, энтальпии, теплоты, энтропии, располагаемой работы и работы объемного расширения
2. Уравнение состояния идеального газа 3. Первый закон термодинамики в различных формах записи с использованием различных параметров и функций (см. п.1) 4. Уравнение политропного и других характерных процессов идеального газа, их графики в p-v и Т-s координатах, особенности превращения энергии в этих процессах 5. Первый закон термодинамики для потока 6. Уравнение неразрывности 7. Понятие сопла и диффузора, их характерные признаки 8. Понятие «критический режим истечения из сопла», зависимость изменения основных термодинамических параметров и функций для каналов различного профиля от условий на входе в канал 9. Второй закон термодинамики для простых и для сложных термодинамических систем 10. Диаграмма водяного пара в p-v, T-s, i-s и p-T координатах 11. Термодинамические процессы водяного пара в p-v, T-s и i-s координатах 12. Понятие дросселирования реального газа (пара) и его расчет 13. Понятие «тепловая машина», прямой и обратный циклы, КПД и холодильный коэффициент 14. Принципиальные схемы ДВС, ГТУ, ВРД, ЖРД, паросиловых и холодильных тепловых машин, которые были представлены в теоретической части дисциплины на лекциях, и графические изображения их циклов. Законы идеального газа Некоторые законы идеального газа (законы Бойля-Мариотта и Гей-Люссака) были получены экспериментально в начале 19-го века. В настоящее время целесообразнее рассматривать их как следствие из закона состояния идеального газа, экспериментально установленного Клайпероном позже, в 1834 году. Уравнение Клайперона устанавливает, что для любого идеального газа, в любом его состоянии выполняются равенства:
где p – абсолютное давление [Па]; v – удельный объем [м3/кг]; T – абсолютная температура [К]; R – газовая постоянная;
Уравнение состояния идеального газа массой 1 кг
Для произвольной массы газа:
Физический смысл газовой постоянной R R идеального газа не зависит от параметров, а зависит только от физической природы газа. Она характеризует работоспособность газа. Численно R равна работе, которую совершит 1 кг данного газа, если его нагреть на 1 К при постоянном давлении.
Уравнение Менделеева-Клапейрона для одного моля любого газа:
где
Численно Если воспользоваться следствием из закона Авогадро (моль любого газа при одинаковых р и Т занимает одинаковый объем), то легко можно получить величину универсальной газовой постоянной:
Зная универсальную газовую постоянную, легко рассчитать газовую постоянную любого газа:
где μ – масса моля [кг/моль]; В химической термодинамике (для сложных ТДС) количество вещества в системе часто задают числом молей.
т.о.
Первый закон термодинамики Первый закон термодинамики представляет собой всемирный закон сохранения энергии. Энергия не исчезает и не возникает вновь, она только переходит из одних видов в другие в различных физических и химических процессах. Энергия изолированной системы (системы, которая не обменивается с ОС ни веществом, ни энергией) постоянна. Для неизолированных систем изменение внутренней энергии ТДС равна алгебраической сумме внешних воздействий Уравнение первого закона термодинамики для процессов протекающих в ТДС со многими степенями свободы может быть записано для произвольного процесса так:
В дифференциальной форме для элементарного (бесконечно малого) процесса:
Где dU – бесконечно малое изменение внутренней энергии; dQ, dL, dAi – бесконечно малые количества теплоты, работы объемного расширения и другие виды работ соответственно. Для ТДС с равномерным распределением параметров все уравнения запишутся для удельных величин:
Для простой термодеформационной системы:
Эти уравнения называют основным термодинамическим тождествам или первой формой записи первого закона термодинамики с использованием параметра внутренняя энергия. Рассмотрим уравнение
если к нему добавить и вычесть выражение
т.к.
Поскольку
Рассмотрим форму записи:
Если прибавить и отнять sdT, получаем:
– 3я форма записи первого закона термодинамики с использованием параметра свободная энергия. Рассмотрим форму записи:
Если прибавить и отнять sdT, получаем:
4ая форма записи первого закона термодинамики с использованием параметра свободная энтальпия. Все реальные процессы, протекающие в двигателях, являются неравновесными, однако, в технической термодинамике их заменяют соответствующими равновесными процессами. Зная уравнения первого закона и уравнение состояния газов легко рассмотреть основные процессы – изобарный, изохорный, изотермический, адиабатный и обобщающий – политропный. Из первого закона термодинамики есть важные для термодинамического анализа следствия. Рассмотрим первый закон термодинамики для случая изобарного процесса (процесса, в котором давление постоянно): (р=const, dр=0). В этом процессе теплоемкость равна изобарной теплоемкости с=ср В результате для изобарного процесса уравнение [] запишется следующим образом:
То есть, как для изобарного, так и для любого политропного процесса в простой термодинамической системе справедливо утверждение:
Рассмотрим первый закон термодинамики для случая изохорного процесса (процесса, в котором объем постоянен): (v=const, dv=0). В этом процессе теплоемкость равна изохорной теплоемкости с=сv В результате для изохорного процесса уравнение [] запишется следующим образом:
То есть, как для изохорного, так и для любого политропного процесса в простой термодинамической системе справедливо утверждение:
Если разделить уравнения [] друг на друга, получаем:
Второй закон термодинамики Сущность второго закона ТД Iый закон ТД дает необходимые сведения для составления энергетического баланса в ТД процессах и тепловых машинах. Однако он ничего не говорит о возможности осуществления таких процессов и циклов реальных машин. IIой закон ТД, так же как первый, является экспериментальным. Он показывает направления протекания и пределы осуществимости реальных, следовательно необратимых, процессов. Этот закон имеет много проявлений и соответственно много формулировок. Формулировка Больцмана. Свойство природы – стремиться от состояний менее вероятных к состояниям более вероятным. Наиболее вероятным состоянием ТДС является состояние термодинамического равновесия, при котором внутри нее отсутствуют макроскопические потоки вещества и энергии. Если изолированную систему вывести из состояния ТД равновесия, например, создав разницу температур между ее отдельными частями, то за счет самопроизвольных естественных процессов теплообмена она придет к состоянию равновесия, при котором температура всех тел системы выравнивается, и будет находиться в этом состоянии бесконечно долго, пока не начнется взаимодействие с ОС. Формулировка Клаузиуса. Теплота самопроизвольно может переходить от тел с большей к телам с меньшей температурой и не может сама собой, даровым способом, переходить от тел с меньшей к телам с большей температурой. Оствальд отметил невозможность создания вечного двигателя второго рода, в котором вся подведенная теплота превращается в работу.
Математическое выражение IIго закона ТД. Термический КПД цикла Карно с одной стороны равен
с другой стороны как для любых тепловых машин равен
Þ или учитывая знак
– для обратимого цикла Карно где
Любой обратимый цикл можно разбить адиабатами на бесконечное множество элементарных циклов, состоящих из двух адиабат и двух малых отрезков кривой, ограничивающей цикл. Изменение температуры по отрезкам кривой мало, следовательно в каждом элементарном цикле можно отрезки кривой заменить на изотермы и таким образом исследуемый цикл будет представлять собой большое количество циклов Карно.
Для цикла 1-2-3-4-1
для всего количества циклов
при бесконечном количестве адиабат
- интеграл Клаузиуса. Для произвольного обратимого процесса
КПД необратимого цикла Карно всегда меньше КПД обратимого, и тогда
для произвольного необратимого цикла
для произвольного необратимого процесса
В итоге для цикла Карно- для произвольного цикла- для произвольного процесса- Для адиабатной системы
Если в адиабатной системе протекают естественные самопроизвольные процессы, то такая система стремится к состоянию термодинамического равновесия, т.е. энтропия возрастает Т.о. IIй закон термодинамики называют законом возрастания энтропии. Объединяя Iй и IIй законы термодинамики можно сказать: «энергия изолированной системы постоянна, а ее энтропия увеличивается». 6.2 Объединенные уравнения I го и II го законов термодинамики для простых систем. Условие термодинамического равновесия Для произвольного процесса, как было показано ранее, можно записать
а согласно Iму закону термодинамики
Подставляя одно в другое получим
или
или
Полученные уравнения и есть объединенные уравнения двух законов термодинамики для простых систем, они позволяют получить условие стремления к равновесию не только для адиабатных систем
1) при Из уравнения (1), следует что (Знаки: при неравновесных процессах
2) при Из (2) уравнения следует, что
3) при Из (3) уравнения следует, что
4) при Из (4) уравнения следует, что
5) при Из (5) уравнения следует, что
Таким образом, для не изолированных систем, в зависимости от условий взаимодействия с окружающей средой, протекание в них неравновесных процессов происходит таким образом, в таком направлении, что соответствующая функция состояния системы уменьшается, система стремится к равновесию и при достижении его эта функция состояния достигает своего минимального значения. Поэтому IIй закон термодинамики это не только закон возрастания энтропии, но и закон уменьшения соответствующей функции состояния. Объединенные уравнения I го и II го законов термодинамики для сложных систем Термодинамический метод исследования применим и к сложным системам, состоящих из рабочих тел различного химического состава, находящихся в различных агрегатных состояниях. В системе могут протекать химические реакции и осуществляться фазовые переходы. Компонентой сложной термодинамической системы называют – любое независимое, химически различное вещество, содержание которого не зависит от других компонентов. Фазами называют различные формы одного и того же вещества, отличающиеся физическими свойствами и разделенные видимыми макроскопическими границами. Гомогенной ТДС называется такая система, химический состав и физические свойства которой во всех ее частях одинаковы или изменяются непрерывно (без скачков) от одной точки системы к другой. Гетерогенной – называют систему, состоящую из одной или нескольких компонент, находящихся в различных фазах. (Каждая фаза отделена друг от друга поверхностью раздела, при переходе через которую скачкообразно изменяется химический состав или физические свойства. И гомогенная и гетерогенная система могут состоять из химически активных компонент. Характерным признаком сложной ТДС является перераспределение количества вещества между компонентами и фазами, в результате протекания химических реакций и осуществления фазовых переходов, т.е. масса или количество вещества играет роль координаты состояния в таких процессах. Если сложную ТДС вывести из равновесного состояния, то перераспределение массы может происходить и в полностью изолированной системе. Гиббс ввел в ТД понятие химического потенциала и показал, что причину химических реакций и фазовых переходов следует искать в неоднородностях полей химического потенциала:
где
Химические реакции и фазовые переходы изначально не равновесны, так как переход массы не может быть бесконечно малым. Рассмотрим сложную ТДС, состоящую из
Если вся система обменивается теплотой и работой равновесно, то и каждая компонента обменивается теплотой и работой равновесно. Тогда для отдельной компоненты можно записать
где
тогда
Дополнительное слагаемое
Суммирование аналогичных уравнений для всех компонент дает следующее уравнение
при равновесном обмене теплотой и работой, т.е. можно записать, что
Опыты показывают, что единственная форма энергии, в которую превращается некомпенсированная часть взаимодействия подсистемы Тогда
где
– полное изменение энтропии системы с учетом обратимых и необратимых процессов. Уравнение (1) – является сводным уравнением Iго и IIго законов ТД для сложных ТДС. Оно показывает, что внутренняя энергия сложной системы может изменяться за счет обмена энергии с ОС в виде теплоты, работы и за счет химических реакций и фазовых переходов. Совместное уравнение Iго и IIго законов ТД можно записать, используя функции состояния – энтальпию
Уравнения (1) и (2)-(4) – условия термодинамического равновесия сложных систем, при различных условиях взаимодействия с ОС, могут быть представлены в виде: 1) при Из (1) уравнения следует, что
2) при Из (2) уравнения следует, что
3) при Из (3) уравнения следует, что
4) при Из (4) уравнения следует, что
Эти выражения показывают, что химические реакции и фазовые переходы возможны внутри ТДС только при уменьшении соответствующей функции состояния, при этом в состоянии равновесия функция состояния достигает своего минимального значения. P-v диаграмма водяного пара Пары различных веществ широко применяются во всех областях производства и энергетики. Наибольшее распространение получил водяной пар в связи с его низкой стоимостью, легкодоступностью и нетоксичностью. Водяной пар используется как рабочее тело в паровых турбинах, паровых машинах, как теплоноситель в различных теплообменниках и др. Парообразование – процесс превращения вещества из жидкого состояния в газообразное. Испарение – парообразование, которое происходит при любой температуре со свободной поверхности жидкости или твердого тела. Кипение – процесс парообразование как на свободной поверхности жидкости, так и по всему её объему. Конденсация – переход вещества из газообразного состояния в жидкое. Конденсат – жидкость, полученная при конденсации. Сублимация – процесс преобразования твердого вещества непосредственно в пар. Десублимация – обратный процесс. Насыщенный пар – пар, находящийся в равновесии с жидкостью. Т.е. пар в состоянии, когда число молекул покидающих жидкость равно числу молекул, возвращающихся в неё. Сухой пар – пар, в котором отсутствуют частицы жидкости. Влажный пар – пар, в котором присутствуют частицы жидкости. Насыщенный пар – пар, параметры которого соответствуют параметром насыщения (давлению, температуре, плотности, при которых наступает равновесие твердой и газообразной фаз). Влажный насыщенный пар – пар при температуре и давлении насыщения, в котором содержатся мелкодисперсные взвешенные частицы жидкости. Перегретый пар – пар, находящийся при температуре, величина которой превышает температуру насыщения при данном давлении. Степень сухости – массовая доля сухого насыщенного пара во влажном. Степень влажности – массовая доля кипящей жидкости во влажном паре. Фазовая p-v диаграмма системы, состоящей из жидкости и пара, представляет собой график зависимости удельных объемов воды и пара от давления. Термодинамика потока
Термодинамическая теория течения и истечения газов и паров имеет большое прикладное значение в современной теплоэнергетике. Целый ряд технических расчетов основывается на закономерностях, которые вытекают из рассмотрения и исследования термодинамики процессов течения и истечения газов и паров. С этими закономерностями приходится сталкиваться при изучении процессов в тепловых двигателях, особенно в реактивных двигателях, газовых и паровых турбинах, рабочий процесс которых полностью основывается на закономерностях процессов течения и истечения газов и паров. Массовый расход через сопло Массовый расход через сопло найдем, используя уравнение постоянства расхода
при адиабатном истечении идеального газа
Массовый секундный расход идеального газа зависит от площади выходного сечения канала, начального состояния газа, физической природы рабочего тела и перепада давлений в сопле
рис. 32 Из этого уравнения следует (рис 5в), что при Цикл Карно. Основоположник термодинамики Карно предложил предельные идеальные циклы тепловых машин. Предельным случаем будет тот, когда вся теплота в цикле будет подводиться и отводиться в изотермных процессах. Прямой цикл Карно состоит из двух изотермических процессов подвода и отвода тепла и двух адиабатных процессов расширения и сжатия. КПД цикла Карно определяется на основе уравнения КПД любой тепловой машины []:
Поскольку
Термический КПД цикла Карно не зависит от рабочего тела. КПД зависит только от перепада температур, чем он больше, тем больше КПД
Если
Обратный цикл Карно. Холодильный коэффициент для обратного цикла Карно может быть получен на основе тех же соображений, что и КПД для прямого цикла:
Холодильный коэффициент обратного цикла Карно зависит от абсолютных температур
Идеальные циклы ДВС. Идеализация циклов осуществляется при принятых допущениях. На рис 42 представлены циклы: Отто с подводом тепла при
Рис 42 В этих циклах: 1-2 – адиабатное сжатие рабочего тела; 2-3 – подвод тепла к рабочему телу (для Отто по изохоре; Дизеля – по изобаре; Тринклера – часть по изохоре, а часть по изобаре) 3-4 – адиабатное расширение; 4-1 – отвод тепла по изохоре. Исходными данными для анализа являются: 1) параметры рабочего тела 2) начальные параметры 3) 4) масса рабочего тела.
Анализ цикла Тринклера Из рассмотрения циклов видно, что цикл Тринклера является обобщающим по отношению к циклам Отто и Дизеля. Порядок анализа следующий: 1. Последовательно определяют значения p, v и T в характерных точках по уравнениям [] для соответствующих процессов в двигателе. Например, для цикла Тринклера температура в точке 3:
2. На основании уравнений [] определяют количество подведенной и отведенной теплоты в каждом процессе, а также общее количество подведенной и отведенной теплоты. Например, для цикла Тринклера количество подведенной теплоты:
3. На основании уравнения [] определяют величину КПД цикла. Например, для цикла Тринклера:
4. Определяют работу цикла:
5. Опред
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 73; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.233.83 (0.017 с.) |

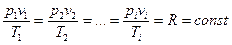
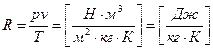
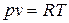
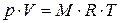
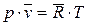
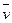 –удельный объем одного моля газа [м3/моль]
–удельный объем одного моля газа [м3/моль]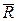 – универсальная газовая постоянная [Дж/мольК]
– универсальная газовая постоянная [Дж/мольК]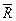 равна работе, которую совершит 1 моль любого газа, если его нагреть на 1 К (при
равна работе, которую совершит 1 моль любого газа, если его нагреть на 1 К (при 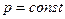 )
)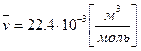
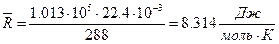
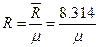
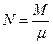
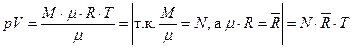
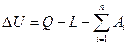
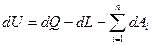
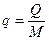 ,
, 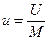 ,
, 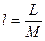 ,
, 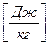
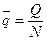 ,
, 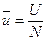 ,
, 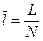
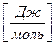
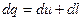
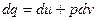 ;
;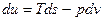 ;
;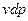 , то получим
, то получим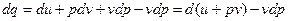
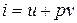 , то
, то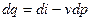
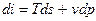
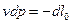 , получаем
, получаем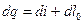
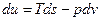 ,
,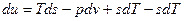
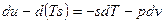
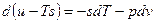
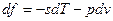
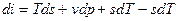
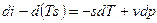
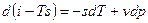
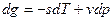
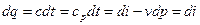
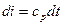
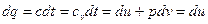
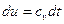
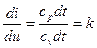 , или
, или 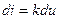
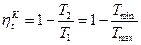 ,
,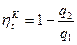 , Þ
, Þ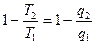 ; Þ
; Þ 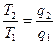 ; Þ
; Þ 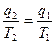
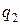 (считая подведенную теплоту
(считая подведенную теплоту 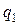 величиной положительной, а отведенную
величиной положительной, а отведенную 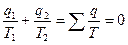
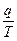 - приведенная теплота.
- приведенная теплота.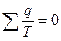 ;
;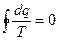
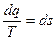
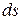 - изменение энтропии (функции состояния).
- изменение энтропии (функции состояния).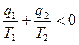 ;
; 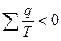

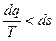 ;
; 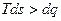 .
. ,
,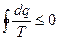 ,
,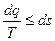 или
или 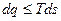 .
.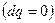 , второй закон термодинамики запишется в виде
, второй закон термодинамики запишется в виде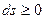
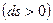 . Когда наступает термодинамическое равновесие
. Когда наступает термодинамическое равновесие 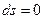 , а
, а 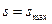
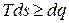 ,
,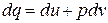 .
.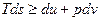
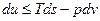
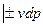
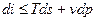
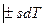
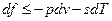
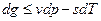
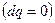 , но и для других условий взаимодействия с окружающей средой.
, но и для других условий взаимодействия с окружающей средой.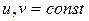
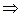
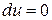 и
и 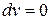 – полная изоляция системы.
– полная изоляция системы.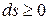
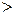 – для неравновесных процессов;
– для неравновесных процессов; 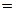 – для равновесных процессов.)
– для равновесных процессов.)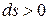 , при достижении термодинамического равновесия
, при достижении термодинамического равновесия 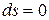 ,
, 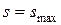 , т.е. если в изолированной системе протекают неравновесные процессы, то система стремится к равновесию.
, т.е. если в изолированной системе протекают неравновесные процессы, то система стремится к равновесию.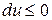 , т.е. при протекании неравновесных процессов внутренняя энергия уменьшается
, т.е. при протекании неравновесных процессов внутренняя энергия уменьшается 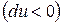 и при достижении термодинамического равновесия
и при достижении термодинамического равновесия 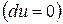 , а внутренняя энергия достигает своего минимального значения
, а внутренняя энергия достигает своего минимального значения 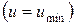 .
.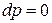 – изобарно-изоэнтропная система.
– изобарно-изоэнтропная система.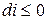 , т.е. при протекании неравновесных процессов энтальпия уменьшается
, т.е. при протекании неравновесных процессов энтальпия уменьшается 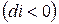 и при достижении термодинамического равновесия
и при достижении термодинамического равновесия 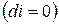 , а энтальпия достигает своего минимального значения
, а энтальпия достигает своего минимального значения 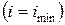 .
.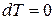 – изохорно-изотермическая система.
– изохорно-изотермическая система.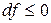 , т.е. при протекании неравновесных процессов свободная энергия уменьшается
, т.е. при протекании неравновесных процессов свободная энергия уменьшается 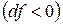 и при достижении термодинамического равновесия
и при достижении термодинамического равновесия 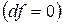 , а свободная энергия достигает своего минимального значения
, а свободная энергия достигает своего минимального значения 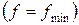 .
.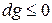 , т.е. при протекании неравновесных процессов свободная энтальпия уменьшается
, т.е. при протекании неравновесных процессов свободная энтальпия уменьшается 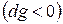 и при достижении термодинамического равновесия
и при достижении термодинамического равновесия 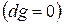 , а свободная энтальпия достигает своего минимального значения
, а свободная энтальпия достигает своего минимального значения 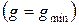 .
.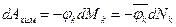
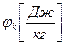 ,
, 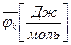 – химический потенциал массовый или мольный;
– химический потенциал массовый или мольный;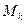 – масса
– масса 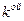 компоненты;
компоненты;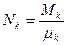 – число молей
– число молей  компоненты.
компоненты.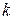 компонент, которая обменивается с окружающей средой теплотой и работой равновесно. Тогда изменение внутренней энергии в целом определится Iм законом ТД.
компонент, которая обменивается с окружающей средой теплотой и работой равновесно. Тогда изменение внутренней энергии в целом определится Iм законом ТД.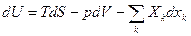
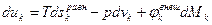
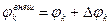
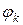 – собственный потенциал компоненты,
– собственный потенциал компоненты, 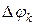 – разность потенциалов между данной компонентой и компонентами всей системы,
– разность потенциалов между данной компонентой и компонентами всей системы,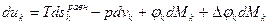 .
.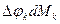 вызвано неравновесностью процесса перераспределения массы, представляет собой некомпенсированную часть взаимодействия, оно всегда положительное. (Опыт показывает, что это потери).
вызвано неравновесностью процесса перераспределения массы, представляет собой некомпенсированную часть взаимодействия, оно всегда положительное. (Опыт показывает, что это потери).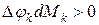
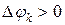 , то имеет место приток массы
, то имеет место приток массы 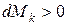 ;
;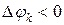 , то имеет место отток массы
, то имеет место отток массы 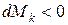 ;
;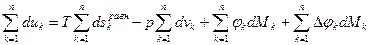
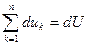
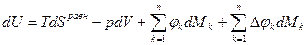 .
.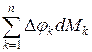 – это теплота, т.е.
– это теплота, т.е. 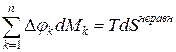 .
.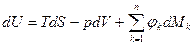
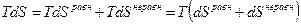
 , свободную энергию
, свободную энергию  и свободную энтальпию
и свободную энтальпию 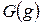 .
.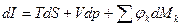
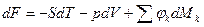
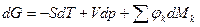
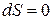 и
и 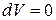 – изохорно-изоэнтропная система.
– изохорно-изоэнтропная система.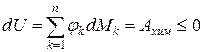 ;
;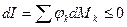 ;
;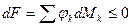 ;
;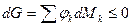 .
.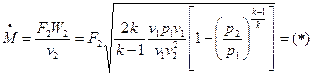
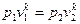 Þ
Þ 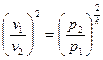 ,
, 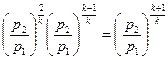
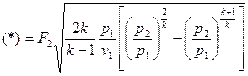
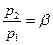 .
.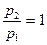 расход
расход 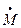 обращается в нуль. С уменьшением давления среды
обращается в нуль. С уменьшением давления среды 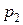 расход газа увеличивается. При некотором отношении
расход газа увеличивается. При некотором отношении 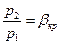 расход газа достигает максимума. При дальнейшем уменьшении отношения
расход газа достигает максимума. При дальнейшем уменьшении отношения 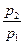 величина
величина 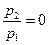 будет снова равна нулю (действительный же массовый расход остается постоянным).
будет снова равна нулю (действительный же массовый расход остается постоянным).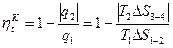
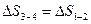 , получаем:
, получаем: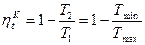
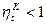 т.к.
т.к. 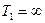 или
или 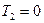 неосуществимо.
неосуществимо.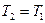 , то
, то 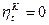 , т.е. при термодинамическом равновесии теплоту невозможно перевести в работу.
, т.е. при термодинамическом равновесии теплоту невозможно перевести в работу.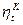 всегда больше
всегда больше 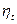 любой машины, работающей в том же диапазоне температур. Поэтому сравнение термических КПД любого цикла и цикла Карно позволяет делать заключение о степени совершенства использования теплоты в машине, работающей по данному циклу.
любой машины, работающей в том же диапазоне температур. Поэтому сравнение термических КПД любого цикла и цикла Карно позволяет делать заключение о степени совершенства использования теплоты в машине, работающей по данному циклу.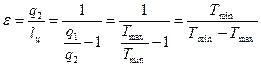
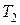 и
и 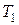 источников теплоты и обладает наибольшим значением по сравнению с холодильным коэффициентом других циклов, протекающих в тех же пределах температур.
источников теплоты и обладает наибольшим значением по сравнению с холодильным коэффициентом других циклов, протекающих в тех же пределах температур. (быстрое горение); Дизеля с подводом тепла при
(быстрое горение); Дизеля с подводом тепла при 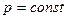 (медленное горение, воздух сжимается в цилиндре двигателя, а жидкое топливо распыляется сжатым воздухом от компрессора); Тринклера с подводом тепла при
(медленное горение, воздух сжимается в цилиндре двигателя, а жидкое топливо распыляется сжатым воздухом от компрессора); Тринклера с подводом тепла при 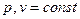 (смешанное горение, Жидкое топливо топливным насосом подается через топливную форсунку в головку цилиндра в виде мельчайших капелек. Попадая в нагретый воздух, топливо самовоспламеняется и горит в течение всего периода, пока открыта форсунка: в начале при постоянном объеме, а затем при постоянном давлении).
(смешанное горение, Жидкое топливо топливным насосом подается через топливную форсунку в головку цилиндра в виде мельчайших капелек. Попадая в нагретый воздух, топливо самовоспламеняется и горит в течение всего периода, пока открыта форсунка: в начале при постоянном объеме, а затем при постоянном давлении).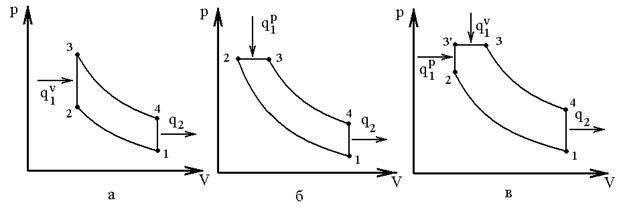
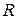 ,
, 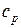 ;
;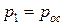 ,
, 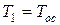 ;
;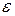 ,
, 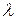 ,
, 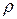 – из опыта конструирования
– из опыта конструирования