
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Суммирование справа в (2. 1. 5) и (2. 1. 6) проводится по повторяющимся индексам, так что эти соотношения в общем случае состоят каждое из девяти уравнений, содержащих по девять коэффициентов.
Обычно принимают гипотезу «парности касательных напряжений», и тогда из симметрии тензоров Из существования упругого потенциала, через который напряжения выражаются производными по деформациям (2.1.1), и из доказанной Риманом теоремы о независимости вторых частных производных от последовательности дифференцирования - следует, что тензоры модулей упругости и податливостей симметричны относительно перестановки первой и второй пары индексов:
В результате оказывается, что из 81 компоненты тензора четвертого ранга в трехмерном пространстве (i, j, k, l = 1, 2, 3) независимыми остаются лишь 21 компонента. Это - сумма цифр на гранях кубика, в который играли еще до нашей эры, а уже много веков позднее, при «изобретении» игральных карт выбрали такие номиналы для валета, дамы, короля, чтобы сумма значений карт одной масти (без туза) была кратна общеизвестному «блэк джек» (в нашей стране - «очко»): 21х3= 63. Вообще, в нашей стране с неограниченными возможностями ограничивать местопребывание большинства людей в избранных зонах неограниченных пространств гимном многих служит «Мурка», а 21 означает только «очко» и уж никак не число независимых констант в тензоре 4-го ранга. Зато – ночью разбуди любого студента – он фамилию свою может не вспомнить, но скажи ему – «очко» и он эхом отзовётся – «двадцать одно». Тензор второго ранга можно записать на листе бумаги или на доске в виде обычной матрицы. Четырехвалентный тензор следовало бы представить в виде четырехмерного куба, который сложно изобразить на бумаге, и даже если изобразишь, то сложно воспринять. Для компьютера такое построение элементарно, для человеческого глаза – бесполезно, поэтому переходят к иной форме записи закона Гука, в которой компоненты тензоров
Отметим также, что в матричной записи традиционно используют техническую сдвиговую деформацию, которая в два раза больше, чем тензорная:
Такая же «путаница» с двойками возникает и при переходе от тензора к матрице податливостей:
Для тензора модулей упругости такие изменения при переходе к матричной записи не возникают, поэтому формулы преобразования для S и E в матричной форме различаются, а в тензорной, естественно, нет. Закон Гука (2.1.6) можно теперь записать так:
Фигурными скобками обозначают «вектор», прямыми – матрицу. Вследствие симметрии относительно диагонали в матрице податливостей независимыми остаются лишь шесть диагональных констант и половина недиагональных, т. е. всего 21 константа:
Несмотря на уменьшение числа индексов, ранги тензоров (второй – для тензора напряжений, и четвертый – для тензора податливостей) остаются прежними, то есть формулы преобразования тензоров и матриц при повороте системы координат будут содержать направляющие косинусы во второй и в четвертой степенях, соответственно.
|
|||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 108; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.188.66 (0.006 с.) |
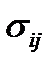 и
и  следует, что тензоры модулей и податливостей не меняются при перестановке внутри первой и второй пары индексов i и j, k и l. При этом число независимых компонент тензоров напряжений и деформаций снижается до шести, а число компонент тензоров модулей и податливостей – с 81 до 36.
следует, что тензоры модулей и податливостей не меняются при перестановке внутри первой и второй пары индексов i и j, k и l. При этом число независимых компонент тензоров напряжений и деформаций снижается до шести, а число компонент тензоров модулей и податливостей – с 81 до 36.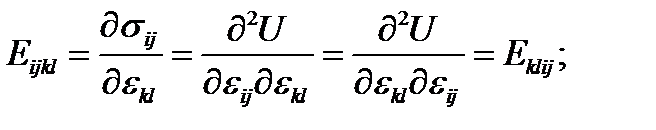
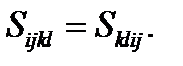 (2.1.7)
(2.1.7)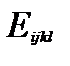 и
и  представляются в виде матриц
представляются в виде матриц  , а шесть компонент тензоров напряжений и деформаций второго ранга записываются в виде вектор-столбцов. При этом пара индексов заменяется на один индекс: 11 → 1; 22 → 2; 33 → 3; 23 → 4; 31 → 5; 12 → 6. Это правило замены связано с использованием только четных циклических перестановок тройки индексов: 123, 231, 312, соответствующих «правой» системе координат. Напомним, что четными называются перестановки с четным или нулевым числом ошибок (ошибка, когда большее число стоит перед меньшим).
, а шесть компонент тензоров напряжений и деформаций второго ранга записываются в виде вектор-столбцов. При этом пара индексов заменяется на один индекс: 11 → 1; 22 → 2; 33 → 3; 23 → 4; 31 → 5; 12 → 6. Это правило замены связано с использованием только четных циклических перестановок тройки индексов: 123, 231, 312, соответствующих «правой» системе координат. Напомним, что четными называются перестановки с четным или нулевым числом ошибок (ошибка, когда большее число стоит перед меньшим).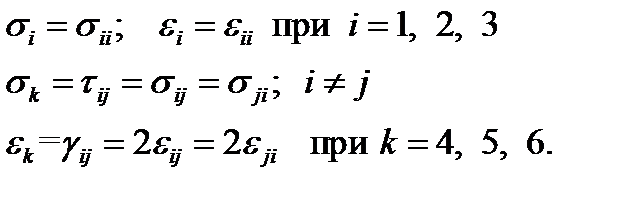 (2.1.8)
(2.1.8)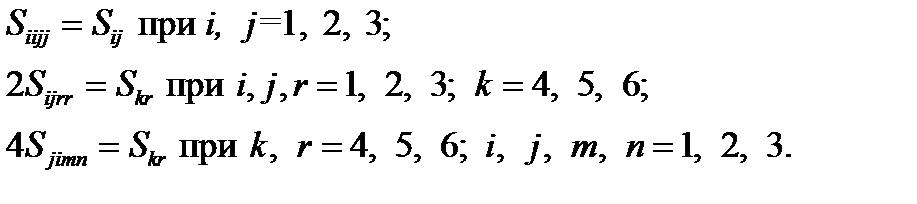 (2.1.9)
(2.1.9)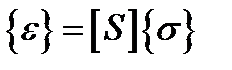 (2.1.10)
(2.1.10) (2.1.11)
(2.1.11)


