
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Механика деформирования композитовСодержание книги
Поиск на нашем сайте
Обобщенный закон Гука в тензорной и матричной формах Определение упругости часто связывают с наблюдаемыми фактами: «если тело нагрузить, а затем разгрузить, то оно вернётся к прежней форме». Интуитивно - понятно, но строго говоря, этого не может происходить, остаточные деформации всегда существуют, иначе, чем вызвана «усталость» – разрушение при многократном нагружении в упругой области. И главное, понятие нагрузки и разгрузки можно строго определить лишь для одноосного нагружения. Только числа можно сравнивать по признаку «больше - меньше». Уже для векторов (а тем более, для тензоров) этого сделать нельзя. И поэтому при комбинированном нагружении, например, растяжением и сдвигом, неясно, что происходит – нагрузка или разгрузка, когда растягивающие напряжения растут, а касательные - убывают. Более правильно говорить, что «упругим называется тело, поведение которого можно с приемлемой точностью описать уравнениями теории упругости», то есть определяющими соотношениями между тензорами напряжений и деформаций, включающими только константы (в линейном случае - модули упругости или податливости). Определение упругости можно дать через наличие упругого потенциала Закон упругости в общем случае имеет вид
где компоненты тензора малых деформаций Коши выражаются через перемещения:
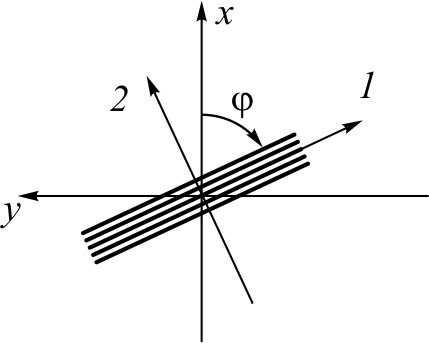
Именно при такой записи деформации (как и напряжения) представляют собой тензор, то есть преобразуются при повороте системы координат (рис. 2.1.1) по правилам преобразования тензоров второго ранга:
Рис. 2.1.1. Схема поворота системы координат
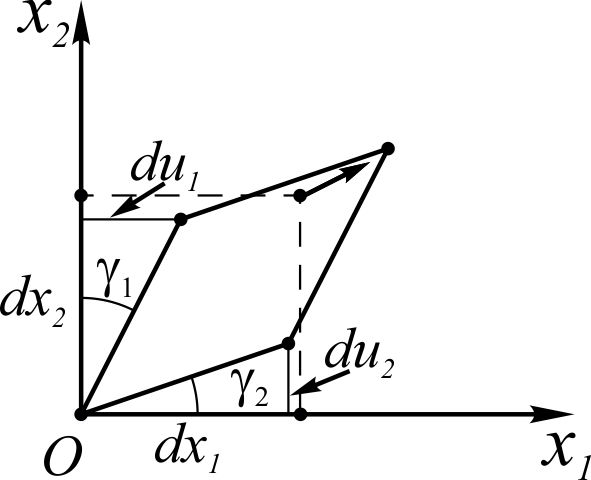
На рис. 2.1.2 дана иллюстрация технической сдвиговой деформации γ12, которую принято определять как «угол, на который изменился прямой угол».
Рис. 2.1.2. Иллюстрация понятия «техническая сдвиговая деформация»
Из рис. 2.1.2 видно, что:
то есть техническая сдвиговая деформация γ12 в два раза больше тензорной ε12, и в этом причина различия тензорной и матричной формы обобщенного закона Гука, который можно записать через тензор модулей упругости четвертого ранга
или – эквивалентно - через тензор упругих податливостей
О задачах теории упругости Полная система уравнений теории упругости кроме определяющих соотношений (2.1.5) или (2.1.6) включает в себя уравнения совместности деформаций (2.1.26) и уравнения равновесия:
где Формулы (2.1.2) выражают 9 компонент тензора малых деформации через три компоненты вектора перемещений. Только шесть компонент деформаций считаются независимыми, как следствие из так называемого «закона парности касательных напряжений». На самом деле, это, конечно, не закон, а гипотеза, ограничивающая класс симметричной теории упругости. Развиваемые вот уже более ста лет моментные теории упругости типа Коссера эту гипотезу не используют и число компонент тензора деформаций увеличивается. Можно ввести также антисимметричный тензор вращения, компоненты которого часто предполагают пренебрежимо малыми:
Тензор
В плоском случае через две компоненты вектора перемещений надо взаимооднозначно определить три компоненты тензора деформаций, поэтому требуется одно уравнение совместности деформаций:
В трехмерном случае можно непосредственно проверить, что из 81 возможного уравнения (2.1.26) из-за симметрии по парам индексов и различия в знаках остаются независимыми только шесть: по три в каждой группе. Полагая i = k =1, j =s=2, получаем первую группу уравнений типа (2.1.27), а при i = k =1, j =2, s =3 – вторую группу:
В (2.1.27) и (2.1.28) выписаны лишь первые варианты уравнений каждой группы, по два других получаются формально – круговой перестановкой индексов 1 →2→3. Для решения задачи теории упругости необходимо задать условия на поверхности тела
В каждой точке
Таким образом, задача теории упругости состоит в решении уравнений при заданных граничных условиях. Если
Тема 2. Механика деформирования композитов
Лекция 2.1. Теория упругости анизотропных сред.
Основная задача механики – это установление связи между причиной и результатом, между силой и движением. Применительно к твердому телу – это связь между векторами усилий Р i и перемещений Напомним, что задать функцию - значит установить (1) соответствие (в частности, взаимооднозначное) между элементами двух множеств и (2) область определения этой функции. Механика деформирования формулирует – (1) – определяющие соотношения, а механика разрушения – в широком смысле – занимается – (2) – установлением области справедливости этих определяющих соотношений, и потому является частью механики твердого тела, хотя и с совершенно другими подходами, чем, скажем, теория упругости. Прежде чем переходить к тензорной записи определяющих соотношений теории упругости анизотропного тела следует уточнить, в каких задачах нужно знание упругих характеристик? Для стержневых и балочных элементов (для статически определимых стержневых конструкций) напряжения зависят только от нагрузок и размеров сечений элементов, и их можно оценивать без учета анизотропных упругих свойств. Разумеется, в общей постановке краевых задач теории упругости знание параметров определяющих соотношений необходимо, и любой стандартный пакет программ (типа ANSYS) запросит значения элементов матрицы модулей упругости и податливостей, но можно отметить пять типов задач, в которых знание упругих характеристик необходимо даже для простейших аналитических расчетов. Каковы же основные области, где необходимо знание упругих характеристик? 1. Расчет несущих или упругих элементов, когда нужно оценить перемещения при заданных нагрузках (балки перекрытия, мосты, листовые рессоры). 2. Задачи устойчивости: возможные формы выпучивания (buckling) стержней, пластин, оболочек и соответствующие критические нагрузки рассчитываются через упругие характеристики. 3. Динамические задачи: в расчетные формулы для скоростей волн и собственных частот колебаний входят упругие характеристики, отнесенные к плотности материала.
4. Задачи о концентрации напряжений. При растяжении изотропной пластины с круговым отверстием теоретический коэффициент концентрации напряжений Kt равен трем, независимо от модуля упругости. Но в анизотропной пластине Kt существенно зависит от упругих свойств и становится – при растяжении в «сильном» направлении – значительно больше, чем в изотропной пластине. 5. Расчет многослойных композитных пластин (см. Лекцию 2.3). Если деформации каждого слоя (в простейшем случае растяжения) считаются одинаковыми, то напряжения в них должны быть пропорциональны модулям упругости каждого слоя и заранее неясно, в каком слое начнётся разрушение. Поэтому, собственно, и развивается весь аппарат теории анизотропной упругости, чтобы пересчитав напряжения в слоях, ответить на главный вопрос прикладной МДТТ: «Разрушится композитная конструкция или нет?».
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.98.190 (0.011 с.) |

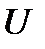 , когда напряженно-деформированное состояние (НДС) в данный момент времени зависит только от текущих значений приложенных усилий и не зависит от пути (или истории) нагружения.
, когда напряженно-деформированное состояние (НДС) в данный момент времени зависит только от текущих значений приложенных усилий и не зависит от пути (или истории) нагружения.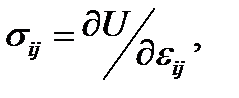 (2.1.1)
(2.1.1)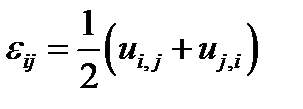 . (2.1.2)
. (2.1.2)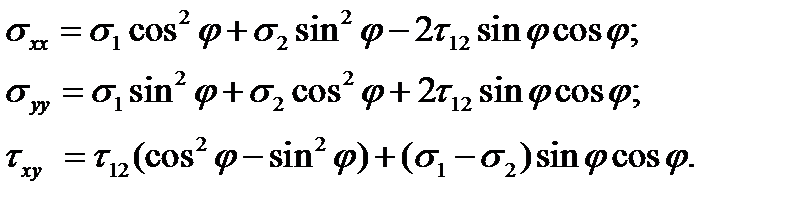
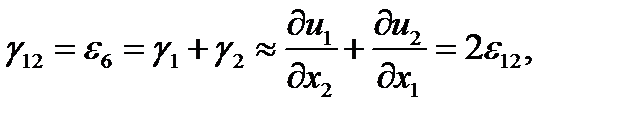
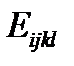 в виде:
в виде: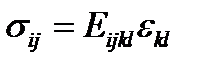 (2.1.5)
(2.1.5)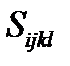 :
: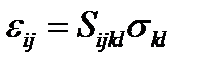 (2.1.6)
(2.1.6)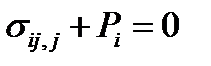 (2.1.24)
(2.1.24)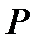 – «массовая» сила (на единицу объема),
– «массовая» сила (на единицу объема), 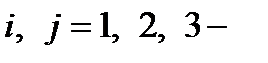 координатные оси.
координатные оси.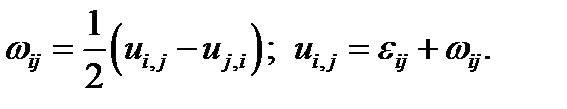
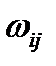 имеет три независимые компоненты: его диагональные члены равны нулю, недиагональные - антисимметричны. Чтобы обеспечить взаимооднозначное соответствие между девятью производными от трёх компонент вектора перемещений по трём координатам (или девятью компонентами тензоров (2.1.24), (2.1.25) и тремя компонентами вектора перемещений необходимо ввести шесть уравнений совместности деформаций. Их общее выражение – без вывода – имеет вид:
имеет три независимые компоненты: его диагональные члены равны нулю, недиагональные - антисимметричны. Чтобы обеспечить взаимооднозначное соответствие между девятью производными от трёх компонент вектора перемещений по трём координатам (или девятью компонентами тензоров (2.1.24), (2.1.25) и тремя компонентами вектора перемещений необходимо ввести шесть уравнений совместности деформаций. Их общее выражение – без вывода – имеет вид: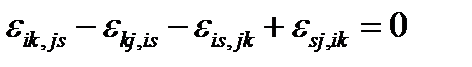 .
.
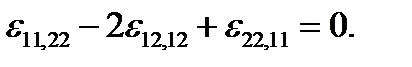
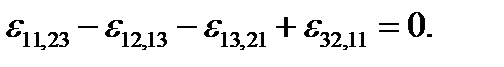
 состоящей из двух частей:
состоящей из двух частей: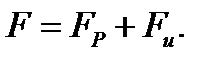 (2.1.29)
(2.1.29)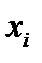 поверхности задано либо перемещение, либо распределенные усилия:
поверхности задано либо перемещение, либо распределенные усилия: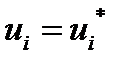 при
при 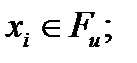 (2.1.30)
(2.1.30)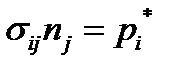 при
при 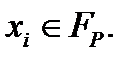 (2.1.31)
(2.1.31)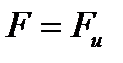 , следовательно, на всей поверхности тела заданы перемещения, соответствующая задача называется первой основной задачей теории упругости. Если
, следовательно, на всей поверхности тела заданы перемещения, соответствующая задача называется первой основной задачей теории упругости. Если 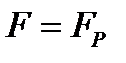 и на всей поверхности заданы распределенные усилия, будем говорить о второй основной задаче. Сформулированная выше постановка (2.1.29) - (2.1.31) относится к смешанной задаче.
и на всей поверхности заданы распределенные усилия, будем говорить о второй основной задаче. Сформулированная выше постановка (2.1.29) - (2.1.31) относится к смешанной задаче.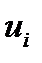 , через которые можно выразить тензоры напряжений
, через которые можно выразить тензоры напряжений 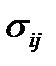 и деформаций
и деформаций 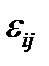 . Механика деформируемого твердого тела (МДТТ) обосновывает: определяющие соотношения, связывающие между собой тензоры напряжений и деформаций, и границу справедливости этой связи.
. Механика деформируемого твердого тела (МДТТ) обосновывает: определяющие соотношения, связывающие между собой тензоры напряжений и деформаций, и границу справедливости этой связи.


