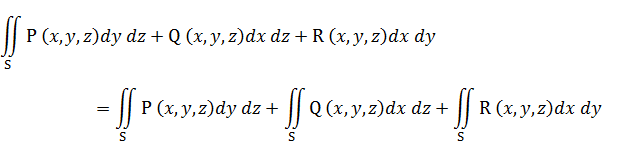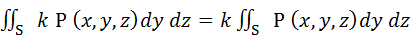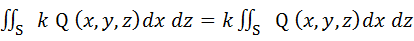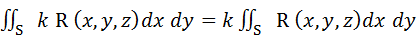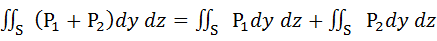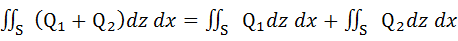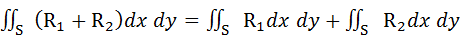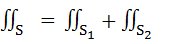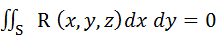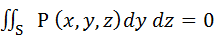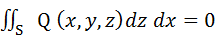Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
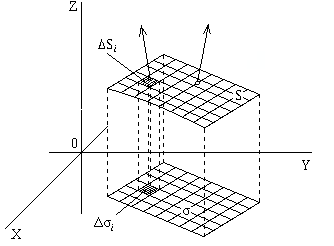
Поверхностный интеграл второго рода.Содержание книги Поиск на нашем сайте Пусть S – двухсторонняя ограниченная поверхность, заданная уравнением z = f (x, y), где f (x, y) – непрерывная функция в замкнутой области D – проекции поверхности S на плоскость XOY, а R (x, y, z) – непрерывная функция на поверхности S. Выберем верхнюю сторону поверхности S. Разобьем поверхность S сетью кусочно-гладких линий на n частей Δ S 1, Δ S 2, …, Δ Sn. Проекциями этих линий на плоскость XOY область D разобьется на n областей, обозначим их соответственно Δσ1, Δσ2, …, Δσ n. Возьмем на каждой части Δ Si произвольную точку Mi (ξ i,η i,ζ i) и составим интегральную сумму:
рис. 3.1
Так как сторона поверхности выбрана верхняя, то (Δ Si) xy = Δσ i, а значит
В правой части равенства имеем интегральную сумму для двойного интеграла от непрерывной функции R (x, y, f (x, y)) по области Dxy. При стремлении к нулю шага разбиения поверхности S, Δσ i также стремится к нулю. В пределе получаем формулу
определяющую интеграл по верхней стороне поверхности S по переменным x и y через двойной интеграл по ее проекции на плоскость XOY. Аналогичным образом устанавливается справедливость формул:
для функции P (x, y, z), непрерывной на двухсторонней поверхности S, заданной уравнением x = f (x, y) (Dyoz – проекция поверхности S на плоскость YOZ) и
для функции Q (x, y, z), непрерывной на двухсторонней поверхности S, заданной уравнением y = f (x, z). Если поверхность S такова, что для функций P (x, y, z), Q (x, y, z) и R (x, y, z), определенных в точках этой поверхности, интегралы (3.1), (3.2) и (3.3) существуют, то вводится понятие поверхностного интеграла «общего» вида по выбранной стороне поверхности:
Свойства поверхностных интегралов второго рода. А) При перемене стороны поверхности S знак поверхностного интеграла второго рода меняется на противоположный. Б) Постоянный множитель можно выносить за знак поверхностного интеграла: В) Поверхностный интеграл от суммы двух функций равен сумме соответствующих интегралов слагаемых: Г) Если поверхность S разбита на части S 1 и S 2, то интеграл по всей поверхности S равен сумме интегралов по ее частям: Д) Если S – цилиндрическая поверхность с образующими, параллельными оси OZ, то Если S – цилиндрическая поверхность с образующими, параллельными оси OX, то Если S – цилиндрическая поверхность с образующими, параллельными оси OY, то Вычисление поверхностных интегралов второго рода. К вычислению поверхностных интегралов второго рода приводит задача о потоке векторного поля. Существует несколько основных методов вычисления поверхностных интегралов второго рода.
|
||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.006 с.) |

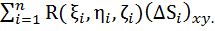
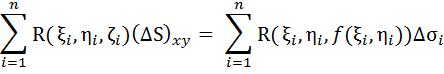
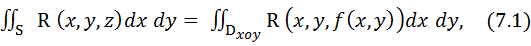 (3.1)
(3.1)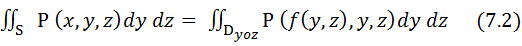 (3.2)
(3.2) 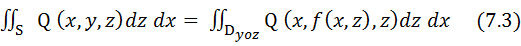 (3.3)
(3.3)