
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический и физический смысл производной функции.Содержание книги
Поиск на нашем сайте Геометрический смысл производной. Угловой коэффициент касательной к кривой
Уравнение касательной к кривой
Определение 8.7. Прямая, проходящая через точку касания перпендикулярно касательной, называется нормалью к кривой в данной точке. Уравнение нормали к кривой
Пример 8.9. Найти уравнение касательной и нормали к кривой Решение: Для того чтобы найти угловой коэффициент касательной, необходимо вычислить производную от заданной функции:
Значение производной в заданной точке M и определяет искомый угловой коэффициент:
Уравнение касательной: Уравнение нормали: Физический смысл производной. Значение производной от функции в данной точке характеризует скорость изменения функции в этой точке по сравнению со скоростью возрастания независимого переменного, в частности, скорость
а ускорение
или вторая производная от пути, т.е.
Пример 8.10. Точка движется по прямой, причем расстояние Решение: Используя физический смысл производной, находим, что скорость движения в любой момент времени определяется формулой Задания для самостоятельной работы по теме «Производная функции». Задание 1. Используя определение производной, доказать справедливость следующих формул:
Задание 2. Найти производные следующих простых функций:
Задание 3. Найти производные следующих сложных функций:
Задание 4. Найти производные функций, заданных неявно и параметрически:
Задание 5. Найти значение производной функции в данной точке:
Задание 6. Найти уравнение касательной к кривой в точке M:
Задание 7. Найти уравнение нормали к кривой в точке M:
Задание 8. Определить угол, под которым кривая пересекает ось абсцисс:
Задание 9. Точка движется попрямой, причем расстояние Задание 10. Путь, проходимый телом, свободно падающим в пустоте, определяется по формуле Задание 11. Радиус шара возрастает равномерно со скоростю 10 см/с. С какой скоростью растет объем шара в момент, когда радиус его составит 100 см? Задание 12. На кривой Задание 13. При каком значении x ордината кривой
Ответы
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |

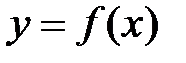 в точке с абсциссой
в точке с абсциссой  равен производной функции
равен производной функции 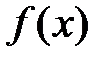 в этой точке, т.е.
в этой точке, т.е.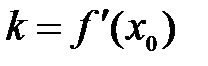 .
.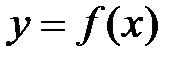 в точке касания
в точке касания 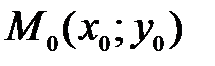 имеет вид:
имеет вид: .
. в точке касания
в точке касания  имеет вид:
имеет вид: .
.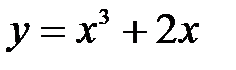 в точке
в точке  .
.
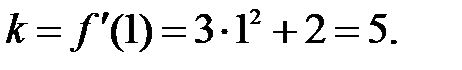
 или
или  .
. или
или  .
. прямолинейного движения есть производная от пути по времени
прямолинейного движения есть производная от пути по времени 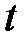 , т.е.
, т.е.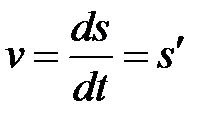 ,
, есть производная от скорости, т.е.
есть производная от скорости, т.е.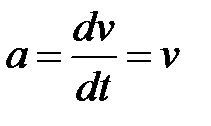 ,
, .
. точки от начала отсчета, измеряемое в метрах, определяется по формуле
точки от начала отсчета, измеряемое в метрах, определяется по формуле 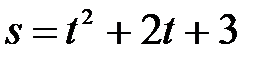 , где
, где 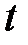 – время, измеряемое в секундах. Определить скорость движения точки в конце пятой секунды.
– время, измеряемое в секундах. Определить скорость движения точки в конце пятой секунды.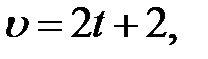 а скорость движения в конце пятой секунды
а скорость движения в конце пятой секунды  (м/с).
(м/с). .
.
 .
.

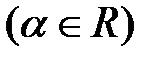 .
.
 .
.
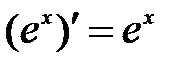 .
.
 .
.
 .
.
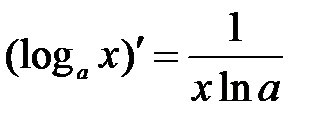 .
.
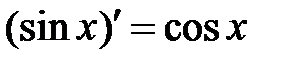 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
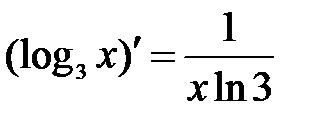 .
.

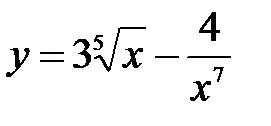 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
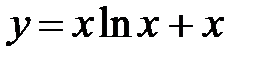 .
.
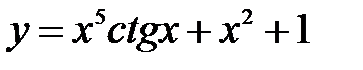 .
.
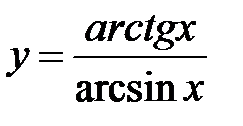 .
.
 .
.
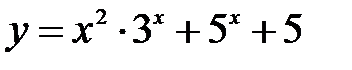 .
.
 .
.
 .
.
 .
.
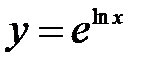 .
.
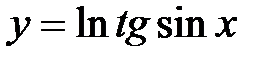 .
.
 .
.
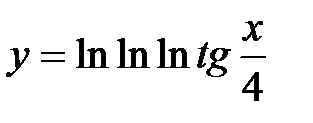 .
.
 .
.
 .
.
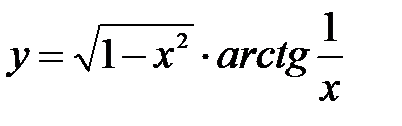 .
.

 .
.
 .
.
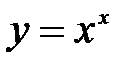 .
.
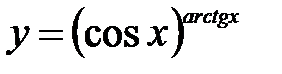 .
.
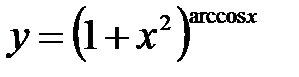 .
.
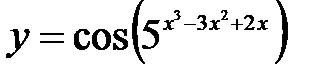 .
.
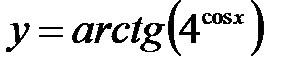 .
.

 .
.
 .
.
 .
.
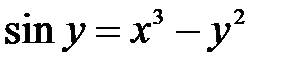 .
.
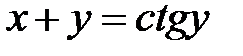 .
.
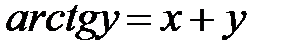 .
.
 .
.
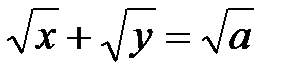 .
.
 .
.
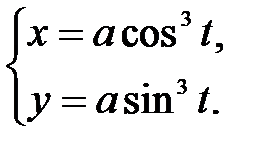

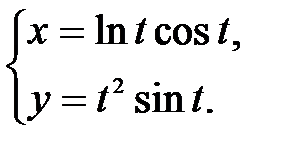
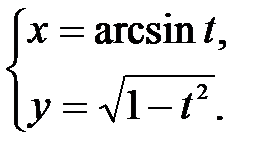
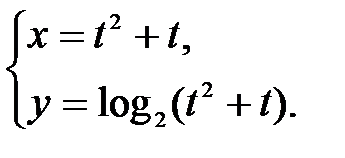

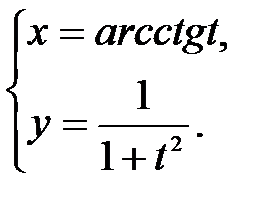

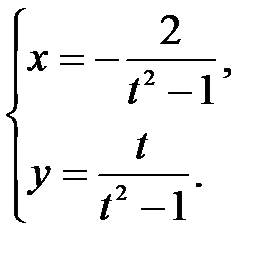
 в точке
в точке  .
.
 в точке
в точке  .
.
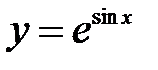 в точке
в точке  .
.
 в точке
в точке  .
.
 в точке
в точке 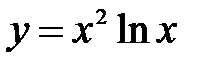 в точке
в точке  ,
,  .
.
 ,
, 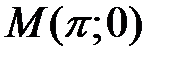 .
.
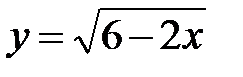 ,
,  .
.
 ,
,  .
.
 M при
M при 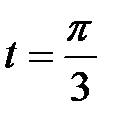 .
.
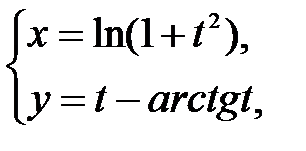 M при
M при 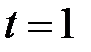 .
.
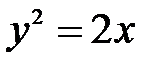 ,
,  .
.
 ,
, 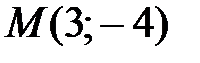 .
.
 ,
,  .
.
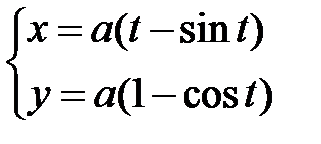 , M при
, M при 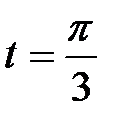 .
.
 .
.
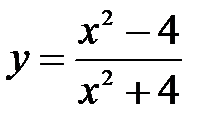 .
.
 .
.
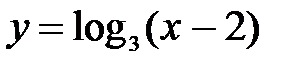 .
.
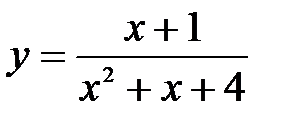 .
.
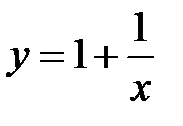 .
.
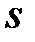 точки от начала отсчёта, измеряемое в метрах, определяется по формуле
точки от начала отсчёта, измеряемое в метрах, определяется по формуле 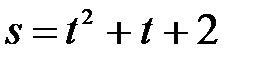 , где
, где  – время, измеряемое в секундах. Определить скорость движения точки в конце третьей секунды.
– время, измеряемое в секундах. Определить скорость движения точки в конце третьей секунды.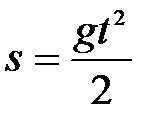 . При этом предполагается, что в начальный момент времени тело находится в начале отсчета и начальная скорость равна нулю; g – ускорение свободного падения. Вывести закон изменения скорости свободно падающего тела.
. При этом предполагается, что в начальный момент времени тело находится в начале отсчета и начальная скорость равна нулю; g – ускорение свободного падения. Вывести закон изменения скорости свободно падающего тела.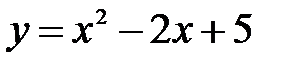 найти точку, в которой ордината возрастает в четыре раза быстрее, чем абсцисса.
найти точку, в которой ордината возрастает в четыре раза быстрее, чем абсцисса.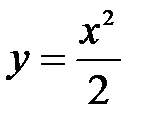 будет возрастать в четыре раза быстрее, чем ордината кривой
будет возрастать в четыре раза быстрее, чем ордината кривой 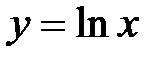 ?
?


