Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разработка двоичного счётчикаСодержание книги Поиск на нашем сайте
Разработать двоичный счётчик на микросхемах К555ИЕ7 (SN74LS193) – группа 1; К555ИЕ5 (SN74LS93) – группа 2; К555ИЕ18 (SN74LS163) – группа 3; К555ИЕ17 (SN74LS169) – группа 4 с коэффициентом счёта, равным n. Моделирование работы счётчика. Пример разработки двоичного счётчика
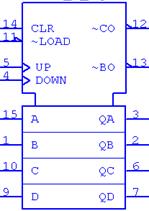
Необходимо реализовать двоичный счётчик на микросхемах К555ИЕ7 (SN74LS193) с коэффициентом счёта Ксч = 31 ∙ 3 = 93. Микросхема К555ИЕ7 (SN74LS193) представляет собой четырёхразрядный двоичный счётчик (рисунок 2.13).
а) б)
Рисунок 2.13 – Условное обозначение микросхем К555ИЕ7 (а) и SN74LS193 (б)
Выводы 15, 1, 10, 9 предназначены для предварительной установки счётчика при нулевом уровне сигнала на входе 11. Высокий уровень напряжения на входе 11 (+5 В) исключает предварительную установку. Вход 5 используется для прямого счёта, а вход 4 – для обратного. Сброс счётчика осуществляется при подачи высокого уровня напряжения на вход 14. Для увеличения разрядности счётчика используется выход 12 (≥15). Одна микросхема может иметь максимальный коэффициент счёта, равный 16. Две последовательно соединённые микросхемы дадут коэффициент счёта, равный 256. Так как заданный коэффициент счёта Ксч = 31 ∙ 3 = 93, то для построения счетчика-делителя с заданным коэффициентом счёта достаточно двух микросхем. Определим двоичный код заданного коэффициента счёта:
=128 ∙ 0 + 64 ∙ 1 + 32 ∙ 0 + 16 ∙ 1 + 8 ∙ 1 + 4 ∙ 1 + 2 ∙ 0 + 1 ∙ 1.
При поступлении 93-го импульса на вход микросхемы DD 1 на выходах Q i микросхем DD 1 и DD 2 установятся следующие логические сигналы:
DD 2: Q 3 Q 2 Q l Q O; DD 1: Q 3 Q 2 Q l Q O. 0101 1101
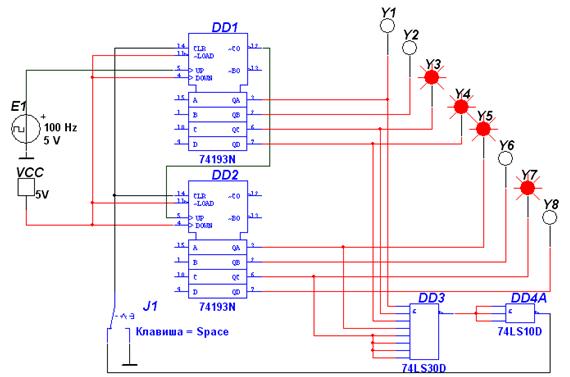
Так как сброс счётчиков в исходное (нулевое) состояние осуществляется сигналом высокого уровня, подаваемым на входы 14, то, объединив с помощью логического элемента 8И-НЕ (DD 3) выходы Qi счетчиков, на которых появятся логические единицы при поступлении на вход 93-го импульса, подадим результирующий сигнал с выхода DD 3, предварительно проинвертировав его с помощью логического элемента 3И-НЕ DD 4 на входы 14 микросхем DD 1 и DD 2. В качестве DD 3 можно использовать микросхему К555ЛА2 (74LS30D), в которой содержится один логический элемент 8И-НЕ; в качестве DD 4 – микросхему К555ЛА4 (74LS10D), в которой содержится два логических элемента 3И-НЕ. Модель разработанной схемы счётчика в среде Multisim приведена на рисунке 2.14. Данная схема осуществляет подсчёт 93-х импульсов и отображение их двоичного кода. С приходом 93-го импульса выходы счётчиков обнуляются и счёт возобновляется.
Рисунок 2.14 – Модель двоичного счётчика с коэффициентом счёта Ксч = 93 Разработка двоично-десятичного счётчика Разработать двоично-десятичный счётчик на микросхемах К555ИЕ6 (SN74LS192) – группа 1; К555ИЕ9 (SN74LS160) – группа 2; К555ИЕ2 (SN74LS90) – группа 3; К555ИЕ20 (SN74LS390) – группа 4 с коэффициентом счёта, равным n. Пример разработки двоично-десятичного счётчика
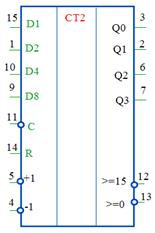
Необходимо реализовать двоично-десятичный счётчик на микросхемах К555ИЕ6 (SN74LS1932) с коэффициентом счёта Ксч = 31 ∙ 3 = 93. Микросхема К555ИЕ6 (SN74LS192) по назначению выводов аналогична микросхеме К555ИЕ7 (SN74LS193) (см. рисунок 2.13). Однако подсчёт числа импульсов осуществляет в двоично-десятичном коде. Одна микросхема может иметь максимальный коэффициент счёта, равный 10. Две последовательно соединённые микросхемы дадут коэффициент счёта, равный 100. Так как заданный коэффициент счёта Ксч = 31 ∙ 3 = 93, то для построения счетчика-делителя с заданным коэффициентом счёта достаточно двух микросхем. Определим двоично-десятичный код заданного коэффициента счёта. При этом каждый из разрядов десятичного числа представляется двоичным кодом из четырёх разрядов:
При поступлении 93-го импульса на вход микросхемы DD 1 на выходах Q i микросхем DD 1 и DD 2 установятся следующие логические сигналы:
DD 2: Q 3 Q 2 Q l Q O; DD 1: Q 3 Q 2 Q l Q O. 1001 0011
Так как сброс счётчиков в исходное (нулевое) состояние осуществляется сигналом высокого уровня, подаваемым на входы 14, то, объединив с помощью логического элемента 8И-НЕ (DD 3) выходы Q i счетчиков, на которых появятся логические единицы при поступлении на вход 93-го импульса, подадим результирующий сигнал с выхода DD 3, предварительно проинвертировав его с помощью логического элемента 3И-НЕ DD 4 на входы 14 микросхем DD 1 и DD 2. В качестве DD 3 можно использовать микросхему К555ЛА2 (74LS30D), в которой содержится один логический элемент 8И-НЕ; в качестве DD 4 –микросхему К555ЛА4 (74LS10D), в которой содержится два логических элемента 3И-НЕ. Модель разработанной схемы счётчика в среде Multisim приведена на рисунке 2.15. Данная схема осуществляет подсчёт 93-х импульсов и отображение их двоично-десятичного кода. С приходом 93-го импульса выходы счётчиков обнуляются и счёт возобновляется. Для отображения двоично-десятичного кода воспользуемся семисегментными индикаторами DCD_HEX.
Рисунок 2.15 – Модель двоично-десятичного счётчика с коэффициентом счёта Ксч = 93
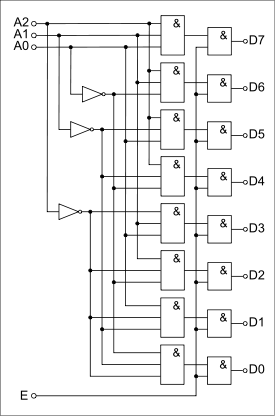
Дешифратор [2] Дешифра́тор (декодер), от англ. Decoder – комбинационная схема, преобразующая n -разрядный двоичный, троичный или k -й код в Двоичный дешифратор работает по следующему принципу. Пусть дешифратор имеет N входов, на которые подаётся двоичное слово Функционирование одноединичного дешифратора, где активные выходные сигналы принимают значение логической 1, описывается системой конъюнкций:
…
Часто дешифраторы дополняются входом разрешения работы Функционирование одноединичного дешифратора с дополнительным входом
…
Обычно микросхемы дешифраторов выполняют с инверсными выходами. У такого дешифратора активный выбранный разряд принимает значение логического нуля. Двоичное слово на входе дешифратора часто называют адресом. Таблица истинности двухвходового двоичного дешифратора с четырьмя выходами (
Таблица 2.7 – Таблица истинности двухвходового двоичного дешифратора
Таблица 2.8 – Дешифратор с тремя входами адреса и входом разрешения на восемь выходов 23
Далее будет детально рассмотрен дешифратор, преобразующий двоичный код в десятичный код, подаваемый на семисегментный индикатор. Микросхема SN74LS248 D представляет собой дешифратор, преобразующий входной двоичный код в выходной десятичный (шестнадцатеричный). К выходу дешифратора подключают семисигментный индикатор с общим катодом.
Рисунок 2.16 – Условное обозначение микросхемы SN74LS192
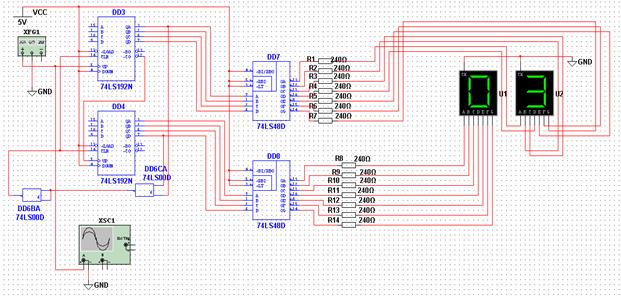
На рисунке 2.16 приняты следующие обозначения: A–D – входная шина данных; QA–QG – выходная шина данных; LT – вход для проверки работоспособности; RBO, RB1 – входы управления. Для начала работы необходимо подать на них сигнал высокого уровня. Схема моделирования двухразрядного двоично-десятичного счетчика с дешифраторами и индикаторами представлена на рисунке 2.17.
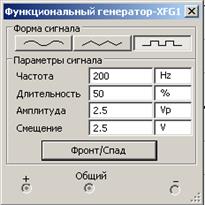
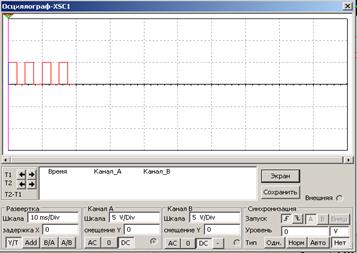
Рисунок 2.17 – Модель двоично-десятичного счётчика с индикацией с коэффициентом счёта Ксч = 81 Импульсы для счета формируются функциональным генератором XFG1 (рисунок 2.18) и подаются на суммирующий вход UP первого счетчика DD 3 (если подавать импульсы на вход DOWN, то счет будет вестись в обратном направлении). Счетные импульсы на вход старшего счетчика DD 4 подаются с выхода переполнения первого счетчика. Выходной сигнал счетчиков в виде параллельного двоичного кода поступает на выводы QA, QB, QC, QD, которые соединены со входами дешифраторов DD 7, DD 8. Преобразованный сигнал с дешифраторов подается на семисегментные индикаторы и отображается в удобном виде.
Рисунок 2.18 – Параметры счетных импульсов и их осциллограмма
Задания для выполнения 1 Рассчитать схему счетчика с заданным коэффициентом счета (таблица 2.9) согласно рисунку 2.15. 2 Выполнить моделирование счетчика согласно рисунку 2.17. 3 Убедиться, что реализуется заданный коэффициент счета.
Таблица 2.9 – Исходные данные к заданию 2
Продолжение таблицы 2.9
Окончание таблицы 2.9
Список литературы 1 Сборник задач по электротехнике и основам электроники / Под ред. В. Г. Герасимова. – М.: Высш. шк., 1987. – 288 с. 2 Лачин, В. И. Электроника: учеб. пособие / В. И. Лачин, Н. С. Савелов. – 7-е изд., перераб. и доп. – Ростов н/Д: Феникс, 2009. – 703 с. 3 Клочков, М. И. Расчет элементов и моделирование схем энергетической и информационной электроники: учеб. пособие / М. И. Клочков. – Хабаровск: ДВГУПС, 2004. – 138 c. 4 Марченко, А. Л. Основы электроники: учеб. пособие для вузов / А. Л. Марченко. – М.: ДМК Пресс, 2008. – 296 с. 5 Москатов, Е. А. Справочник по полупроводниковым приборам / Е. А. Москатов – М.: Радио, 2005. – 208 с. 6 Панфилов, Д. И. Электротехника и электроника в экспериментах и упражнениях. Лаборатория на компьютере: в 2 т. / Д. И. Панфилов, В. С. Иванов, И. Н. Чепурин. – 2-е изд., перераб. И доп. – М.: МЭИ, 2004. – 304 с.
Приложение А (справочное) Таблица А.1 – Параметры биполярных транзисторов
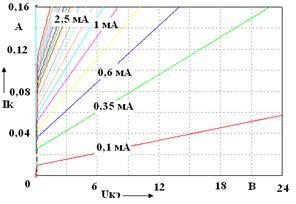
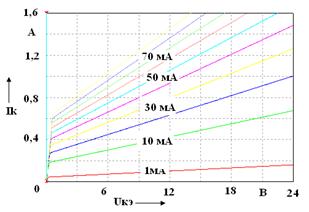
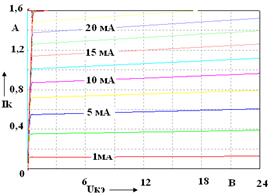
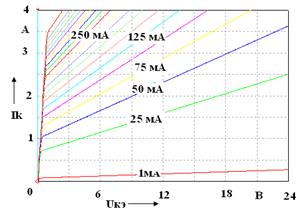
а – ВС547A (КТ3102Б); б – BD135 (КТ815Б); в – 2N2218 (КТ928А); г – BD237 (КТ817Г) Рисунок А.1 –Выходные характеристики биполярных транзисторов
Приложение Б (справочное)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 1052; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.231 (0.007 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


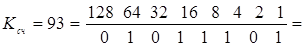
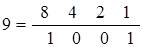 = 8 ∙ 1 + 4 ∙ 0 + 2 ∙ 0 + 1 ∙ 1;
= 8 ∙ 1 + 4 ∙ 0 + 2 ∙ 0 + 1 ∙ 1;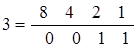 = 8 ∙ 0 + 4 ∙ 0 + 2 ∙ 1 + 1 ∙ 1.
= 8 ∙ 0 + 4 ∙ 0 + 2 ∙ 1 + 1 ∙ 1.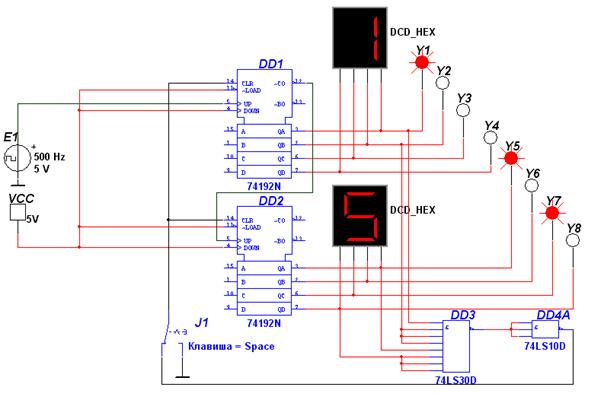
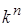 -й одноединичный код, где k – основание системы счисления. Логический сигнал активен на том выходе, порядковый номер которого соответствует двоичному, троичному или k-му коду. Дешифраторы являются устройствами, выполняющими двоичные, троичные логические функции (операции). Наиболее широко распространены дешифраторы преобразующий двоичный код в десятичный код, воспринимаемый человеком.
-й одноединичный код, где k – основание системы счисления. Логический сигнал активен на том выходе, порядковый номер которого соответствует двоичному, троичному или k-му коду. Дешифраторы являются устройствами, выполняющими двоичные, троичные логические функции (операции). Наиболее широко распространены дешифраторы преобразующий двоичный код в десятичный код, воспринимаемый человеком.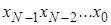 . Тогда на выходах формируется код разрядности, меньшей или равной
. Тогда на выходах формируется код разрядности, меньшей или равной 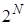 , где разряд, номер которого равен численному представлению входного слова, становится активным (принимает значение логической единицы, логического нуля или переводится в высокоимпедансное состояние – отключается, что зависит от конкретной реализации дешифратора), все остальные разряды неактивны. Очевидно, что максимально возможная разрядность выходного слова равна
, где разряд, номер которого равен численному представлению входного слова, становится активным (принимает значение логической единицы, логического нуля или переводится в высокоимпедансное состояние – отключается, что зависит от конкретной реализации дешифратора), все остальные разряды неактивны. Очевидно, что максимально возможная разрядность выходного слова равна 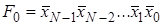
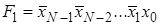
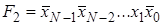
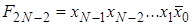
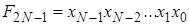 .
.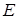 (Enable). Если на этот вход поступает активный логический сигнал (единица или ноль), то один из выходов дешифратора переходит в активное состояние, иначе все выходы неактивны вне зависимости от состояния входов.
(Enable). Если на этот вход поступает активный логический сигнал (единица или ноль), то один из выходов дешифратора переходит в активное состояние, иначе все выходы неактивны вне зависимости от состояния входов.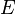 (Enable) описывается системой конъюнкций:
(Enable) описывается системой конъюнкций: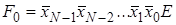
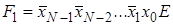
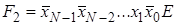
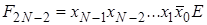
 .
. ) приведена в таблице 2.7.
) приведена в таблице 2.7.