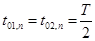Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Получение разностного уравнения ЛНЧ в векторно-матричной формеСодержание книги
Поиск на нашем сайте
Пусть ЛНЧ (линейная непрерывная часть) (рис. **) описывается дифференциальным уравнением в векторно-матричной форме
Общее решение данного дифференциального уравнения записывается в виде
где
Рассмотрим четыре случая работы мостового преобразователя. 1. Транзисторы
Приведем его к нормальной форме Коши. После несложных математических преобразований получим
где
Введем следующий вектор состояния ЛНЧ
Решение векторно-матричного дифференциального уравнения (**) на интервале
где Значение вектора состояния в конце интервала открытого состояния транзисторов
где 2. Транзисторы
Запишем систему уравнений по законам Кирхгофа
Приведем его к нормальной форме Коши. После несложных математических преобразований получим
Матрицы
Решение векторно-матричного дифференциального уравнения (**) на интервале
где Значение вектора состояния в момент времени
где 3. Транзисторы
Приведем его к нормальной форме Коши. После несложных математических преобразований получим
Матрицы
Решение векторно-матричного дифференциального уравнения (**) на интервале
где Значение вектора состояния в момент времени
где 4. Транзисторы
Приведем его к нормальной форме Коши. После несложных математических преобразований получим
Матрицы
Решение векторно-матричного дифференциального уравнения (**) на интервале
где Значение вектора состояния в момент времени
где Для упрощения расчетов будем считать что напряжение питания Используя уравнения (**1) – (**4) получим разностное уравнение ЛНЧ на интервале дискретизации. При преобразовании уравнения учтем, что
Чтобы найти решение этого уравнения необходимо найти длительности
|
||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 108; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 (*)
(*) ,
, - фундаментальная (переходная) матрица состояния,
- фундаментальная (переходная) матрица состояния,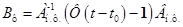 - матрица, учитывающая влияние внешних возмущений,
- матрица, учитывающая влияние внешних возмущений,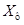 - вектор состояния ЛНЧ.
- вектор состояния ЛНЧ.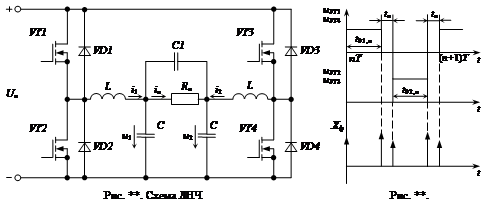
 открыты, а транзисторы
открыты, а транзисторы 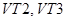 закрыты (рис. **). Интервал
закрыты (рис. **). Интервал 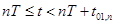 на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **). Источник тока
на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **). Источник тока  учитывает резкие изменения тока на выходе, например, сброс или наброс нагрузки. Для схемы запишем систему уравнений по первому и второму закону Кирхгофа.
учитывает резкие изменения тока на выходе, например, сброс или наброс нагрузки. Для схемы запишем систему уравнений по первому и второму закону Кирхгофа.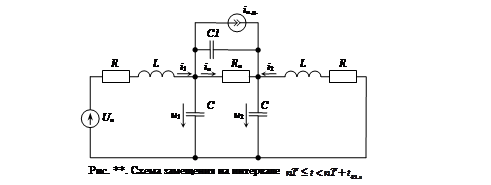
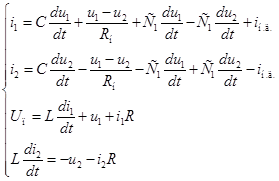

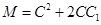 .
. , где Т – знак транспонирования. Вектор внешних воздействий –
, где Т – знак транспонирования. Вектор внешних воздействий – 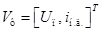 . Тогда матрицы
. Тогда матрицы 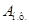 и
и  запишутся:
запишутся: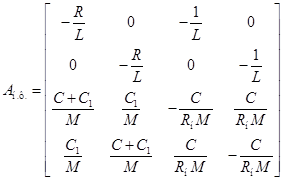
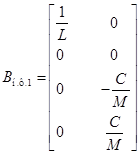
 ,
, ,
, 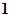 - единичная матрица.
- единичная матрица.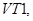
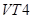 , т.е. при
, т.е. при 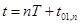 определяется уравнением
определяется уравнением ,(**1)
,(**1)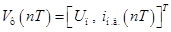 .
.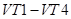 закрыты, ток протекает через диоды
закрыты, ток протекает через диоды 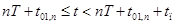 на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **).
на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **).

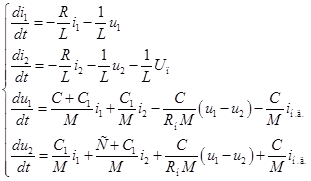
 запишутся:
запишутся:
 ,
, .
.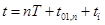 определяется уравнением
определяется уравнением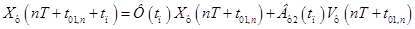 ,(**2)
,(**2) .
.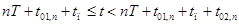 на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **). Для схемы запишем систему уравнений по первому и второму закону Кирхгофа.
на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **). Для схемы запишем систему уравнений по первому и второму закону Кирхгофа.
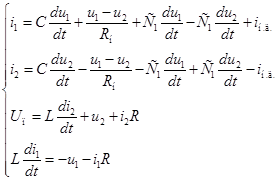

 запишутся:
запишутся:
 ,
,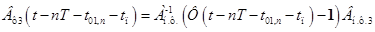 .
. определяется уравнением
определяется уравнением ,(**3)
,(**3) .
.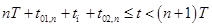 на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **).
на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **).



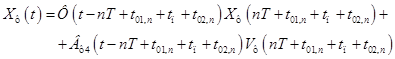 ,
, .
.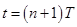 определяется уравнением
определяется уравнением ,(**4)
,(**4)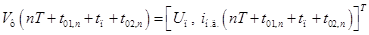 .
.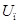 не меняется с течением времени, а изменение дополнительного тока нагрузки
не меняется с течением времени, а изменение дополнительного тока нагрузки 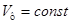 на интервале
на интервале  .
. . В результате преобразования имеем:
. В результате преобразования имеем:
 и
и  . При сигнале задания
. При сигнале задания