
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика расчета электрической цепи постоянного тока на основе законов КирхгофаСодержание книги
Поиск на нашем сайте
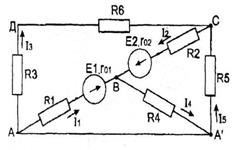
Дано: Е1= 40 В, Е2 = 60 В, R1 = 18 Ом, R2 = 36 Ом, R3 = 16 Ом, R4 = 24 Ом, R5 = 40 Ом, R6 = 34 Ом, r01 = 2 Ом, r02 = 4 Ом.
Для данной электрической цепи выполнить следующее: 1) определить токи во всех ветвях схемы, используя метод узловых и контурных уравнений; 2) составить баланс мощностей для заданной схемы.
1) Составляем систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях. При расчете данным методом произвольно задаем в ветвях направление токов I 1, I 2, I 3, I 4, I 5.
Составляем систему уравнений, применяя законы Кирхгофа. В системе должно быть столько уравнений, сколько в цепи ветвей (неизвестных токов).
В заданной цепи пять ветвей, значит, в системе должно быть пять уравнений (m = 5). Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с n узлами можно составить (n – 1) независимых уравнений. В расчетной цепи три узла (А, В, С), значит число уравнений: n – 1 = 3 – 1 = 2. Составляем два уравнения для любых двух узлов, например, для узлов В и С:
узел В: I 1 + I 2 = I 4, узел С: I 3 +I 5 = I 2. Всего в системе должно быть пять уравнений. Два уравнения уже представлены. Три недостающих составляем для линейно-независимых контуров. Чтобы они были независимыми, в каждый следующий контур надо включить хотя бы одну ветвь, не входящую в предыдущие. Задаемся обходом каждого контура и составляем уравнения по второму закону Кирхгофа.
Контур АДСВА – обход по часовой стрелке: Е2 – Е1 = I2(R2 + r02) – I1(R1 + r01) + I3(R3 + R6).
Контур АВА'А – обход по часовой стрелке: E1 = I1(R1 + r01) + I4R5. Контур А'СВА' – обход против часовой стрелки: Е2 = I2(R2 + r02) + I4 ∙R4 + I5∙R5.
ЭДС в контуре берется со знаком «+», если направление ЭДС совпадает с обходом контура, если не совпадает, то со знаком «–». Падение напряжения на сопротивлении контура берется со знаком «+», если направление тока в нем совпадает с обходом контура, если не совпадает, то со знаком «–».
Получили систему из пяти уравнений с пятью неизвестными:
I2 = I3 + I5 E2 – E1 = I2(R2 +r02) + I3(R3 + R6) – I1(R1 + r01), E1 = I1(R1 + r01) + I4R4, E2 = I2(R2 + r02) + I4R4 + I5R5
Решив систему уравнений, определим величину и направление тока во всех ветвях схемы.
Подставив значения, получим систему уравнений:
I3 + I5 – I2 = 0 20 = 40I2 + 50I3 – 20I1, 40 = 20I1 + 24I4, 60 = 40I2 + 24I4 + 40I5
На основе данной системы уравнений составляем матрицу:
Данную матрицу можно решить различными способами – методом Крамера или методом Гаусса. В результате решения матрицы получаются следующие решения: при x1 = 0,6243 = I1, при x2 = 0,5221 = I2, при x3 = 0,2320 = I3, при x4 = 1,1464 = I4, при x5 = 0,2901 = I5.
Если при решении системы ток получается со знаком «–», значит его действительное направление обратно тому направлению, которым изначально задались. 2) Составляем баланс мощностей для заданной схемы. Источники E1 и Е2 вырабатывают электрическую энергию (работают в режиме генератора), так как направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи запишется так: E1∙I1 + E2∙I2 = I12(R1 + r01) + I22(R2 + r02) + I32(R3 + R6) + I42∙R4 + I52∙R5. Подставляем числовые значения и вычисляем: 40∙0,624 + 60∙0,522 = 0,6242∙(18 + 2) + 0,5222∙(36 + 4) + 0,2322(16 + 34) + + 1,1462∙24 + 0,2902∙40; 56,280 Вт = 56,262 Вт. С учетом погрешности расчетов баланс мощностей сошелся.
Приложение 3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.15 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

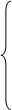 I4 = I1 + I2
I4 = I1 + I2


