Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы распространения светаСодержание книги
Поиск на нашем сайте
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования ОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Им. Ф.М. ДОСТОЕВСКОГО Геометрическая оптика Учебно-методическое пособие по курсам «Оптика» и «Общий физический практикум» Омск 2019 Рецензенты:
К.ф.-м.н. Н.А. Давлеткильдеев (КНИОРП ОНЦ СО РАН) К.ф.-м.н., Г.М. Серопян (ФГБОУ ВО ОмГУ им. Ф.М. Достоевского)
Геометрическая оптика: учебно-методическое пособие по курсам «Оптика и «Общий физический практикум»/ авт.: Б.Т. Байсова, Л.В. Баранова.– Омск: изд-во Ом.гос.ун-та, 2019.–29 с.
В пособии представлены краткие теоретические сведения по разделу волновой оптики «Геометрическая оптика», обеспечивающие выполнение цикла лабораторных работ. Пособие также включает в себя лабораторный практикум и представляет собой самостоятельное руководство к лабораторным занятиям для студентов физического факультета. Практикум содержит описание выполнение лабораторных работ по курсам «Оптика» и «Общий физический практикум». Предназначено для обучающихся по направлениям подготовки бакалавров 03.03.02 «Физика», 03.03.03 «Радиофизика».
ОГЛАВЛЕНИЕ ПРЕДИСЛОВИЕ……………………………………………………………………4 ГЛАВА 1. Основные теоретические сведения……………………...…………..5 1. Законы распространения света …..………………………………..….…5 1.1. Закон независимости световых пучков …………...………………..5 1.2. Закон независимости световых пучков ….…………………...…….5 1.3. Закон отражения света ….……………………………………………5 1.4. Закон преломления света………………………………..………….....6 2. Зеркальное и диффузное отражение ……………………………………….. 7 3. Характеристики центрированной оптической системы………………….. 7 4. Линзы …………………………………………………………………………...12 4.1. Виды линз………………………………………………………….…….12 4.2. Тонкая линза……………………………………………………………..12 4.3. Изображение в линзах…………………………………………………..13 5. Зрительные трубы. Разрешающая способность зрительных труб………13 ГЛАВА 2. Лабораторный практикум…………..……………………………....17 2.1. Измерение фокусных расстояний тонких и толстых линз ….………….....17
2.2. Моделирование зрительных труб ………………………………………..26 СПИСОК ИСПОЛЬЗОВАННОЙ И РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ………………………………………………..………………..…29 ПРЕДИСЛОВИЕ Целью настоящего учебно-методического пособия является ознакомление студентов с основными теоретическими сведениями по теме «Геометрическая оптика» с последующим закреплением теории на практике при выполнении лабораторных работ. Пособие способствует формированию у студентов практических навыков работы на оптическом оборудовании с возможностью наглядного наблюдения изучаемых явлений с последующим оформлением результатов эксперимента. В первой главе изложены краткие теоретические сведения. В представленном теоретическом материале рассмотрены основные законы распространения света, способы получения когерентных волн в оптике, расчет интерференционной картины, интерференция в тонких пленках. Во второй главе представлен лабораторный практикум, включающий пять работ: «Определение длины световой волны с помощью колец Ньютона», «Определение длины световой волны с помощью бипризмы Френеля», «Определение толщины пластинки с помощью наблюдения интерференционных полос равного наклона», «Измерение показателей преломления жидкостей с помощью интерферометра Релея», «Изучение интерференции поляризованных лучей». По каждой работе представлены методические указания о порядке ее выполнения, описание лабораторных установок, а также перечень контрольных вопросов и список рекомендуемой литературы. Геометрическая оптика Геометрическая оптика – это раздел оптики, в котором изучаются законы распространения световой энергии в прозрачных средах на основе представления о световом луче. Световой луч – это линия, имеющая направление, вдоль которого распространяется энергия световых волн. В основу формального построения геометрической оптики положено четыре закона, установленных опытным путем:· закон прямолинейного распространения света;· закон независимости световых лучей;· закон отражения;· закон преломления света. В однородной среде свет распространяется прямолинейно, а на границе раздела сред с разными показателями преломления происходят явления отражения и преломления.
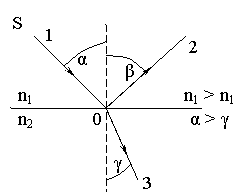
Закон отражения света. Луч света в однородной среде прямолинеен до тех пор, пока он не дойдет до границы этой среды с другой средой. На границе двух сред луч меняет свое направление. Часть света (а в ряде случаев и весь свет) возвращается в первую среду. Это явление называется отражением света. Одновременно свет частично проходит во вторую среду, меняя при этом направление своего распространения - преломляется.
Рис. 1. К закону отражения и преломления
Закон отражения света: Луч падающий 1, луч отраженный 2 и перпендикуляр, восстановленный в точке падения (т. О) к границе двух сред, лежат в одной плоскости. Угол падения α равен углу отражения β: α = β (1)
Закон преломления света. Луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред:
где n12 – относительный показатель преломления второй среды относительно первой. Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления n12 = n2/ n1. Абсолютным показателем преломления среды наз. величина n, равная отношению скорости с электромагнитных волн в вакууме к их фазовой скорости V в среде: n = с / V (3) Среда с большим оптическим показателем преломления называется оптически более плотной. Из симметрии выражения (1) вытекает обратимость световых лучей, сущность которой состоит в том, что если направить световой луч из второй среды в первую под углом β, то преломленный луч в первой среде выйдет под углом α. При переходе света из оптически менее плотной среды в более плотную получается, что sin α > sin β, т.е. угол преломления меньше угла падения света, и наоборот. В последнем случае при увеличении угла падения угол преломления увеличивается в большей мере, так что при некотором предельном угле падения α пр угол преломления становится равным π/2. С помощью закона преломления можно рассчитать значение предельного угла падения: sin α пр/sin(π/2) = n2/n1, откуда α пр = arcsin n2/n1. (4)
В этом предельном случае преломленный луч скользит по границе раздела сред. При углах падения α > α пр свет не проникает в глубь оптически менее плотной среды, имеет место явление полного внутреннего отражения. Угол α пр называется предельным угломполного внутреннего отражения. Явление полного внутреннего отраженияиспользуется в призмах полного отражения, которые применяются в оптических приборах: биноклях, перископах, рефрактометрах (приборах, позволяющих определять оптические показатели преломления), в световодах, представляющих собой тонкие, гнущиеся нити (волокна) из оптически прозрачного материала. Свет, падающий на торец световода под углами, большими предельного, претерпевает на границе раздела сердцевины и оболочки полное внутреннее отражение и распространяется только по световедущей жиле. С помощью световодов можно как угодно искривлять путь светового пучка. Рис.2. Гомоцентрический пучок
Если система не нарушает гомоцентричности пучков, то лучи, вышедшие из точки Р, после прохождения оптической системы пересекутся в некоторой точке Р'. Эта точка является изображением точки Р в оптической системе. Изображение называется действительным, если в точке Р' пересекаются сами лучи, и мнимым, если в точке Р' пересекаются продолжения лучей, проведенные в направлениях, обратных направлению распространения света. Точки Р и Р' называются сопряженными точками. Аналогичным образом две линии или две плоскости называются сопряженными, если одна из них является изображением другой.
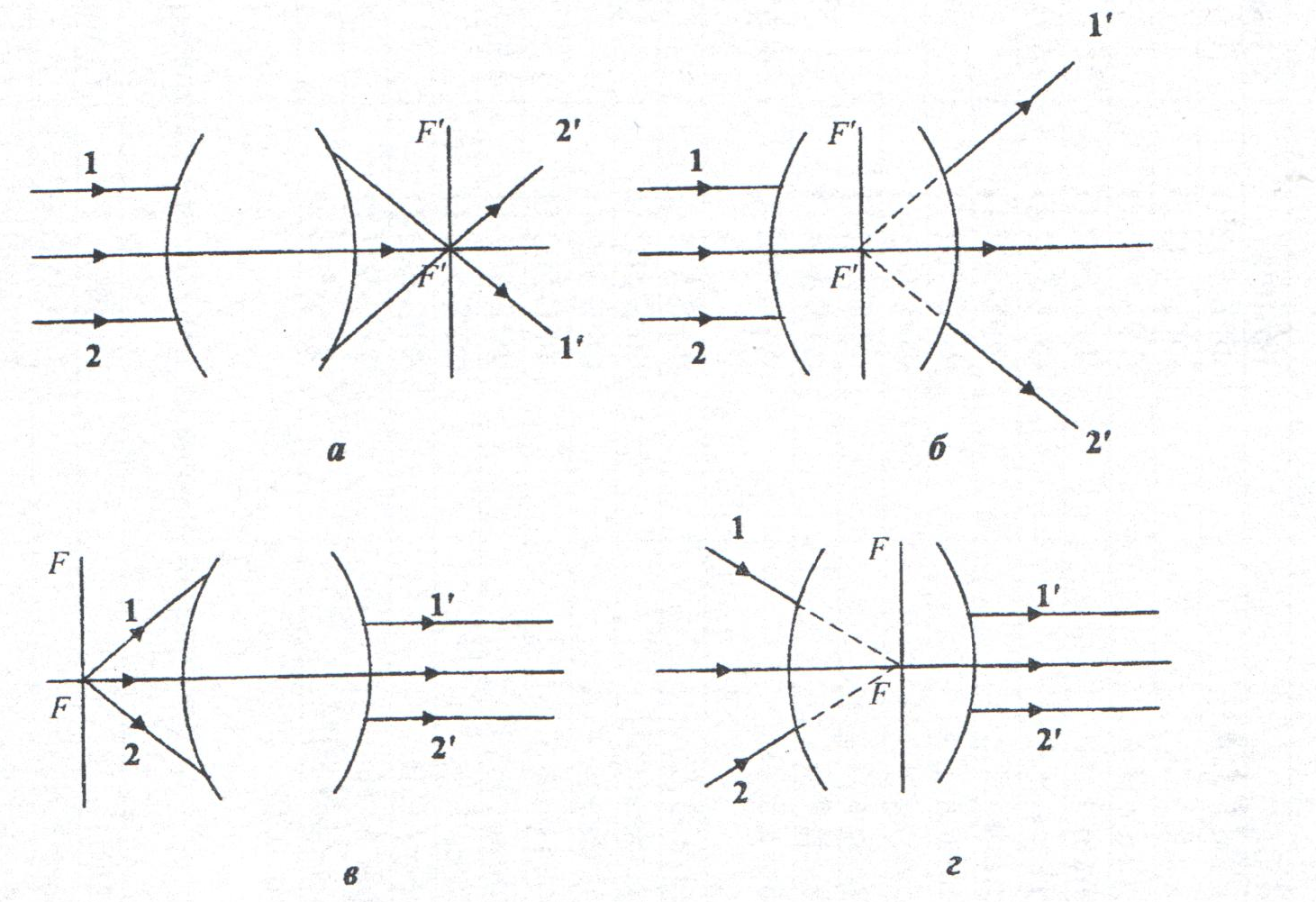
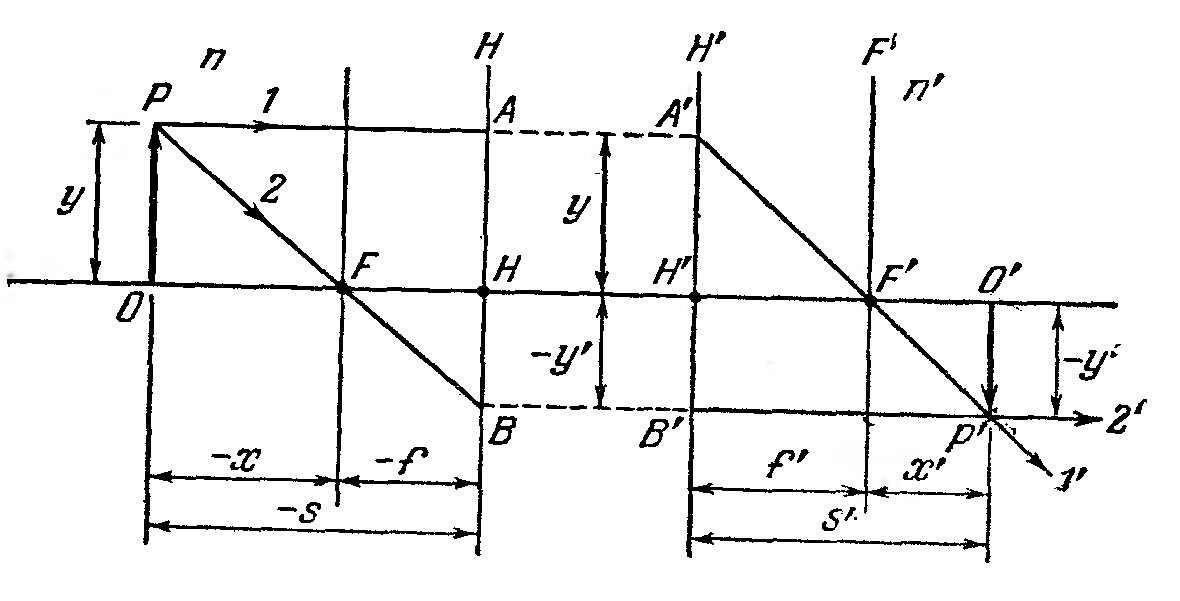
Центрированной оптической системой называется оптическая система, образованная сферическими (в частности плоскими) поверхностями, если центры всех поверхностей лежат на одной прямой. Эта прямая называется оптической осью системы. Если любая точка предмета изображается в виде точки, то изображение называется стигматическим. Оптическая система, которая дает стигматическое изображение, геометрически подобное предмету (имеется в виду, что предмет и изображения лежат в плоскостях перпендикулярных оптической оси системы), называется идеальной. На рис. 3 показаны внешние преломляющие поверхности и оптическая ось некоторой идеальной центрированной оптической системы. Пусть на систему падает пучок лучей, параллельный оптической оси (рис. 3,а; 3,б). Поскольку система идеальна после прохождения оптической системы пучок будет либо сходящимся (рис. 3,а), либо расходящимся (рис.3,б). Точка F', в которой пересекаются сами вышедшие из системы лучи или их продолжения называется задним фокусом оптической системы. Плоскость F'F', проходящая через задний фокус F' и перпендикулярная к оптической оси называется задней фокальной плоскостью. Изображение бесконечно удаленных предметов получается в задней фокальной плоскости оптической системы.
Рис.3. Оптическая система
На оптической оси существует точка F, обладающая таким свойством: вышедшие из нее лучи (рис.3, в) или сходящиеся в ней лучи (рис.3, г) после прохождения через систему становятся параллельными оптической оси. Эта точка называется передним фокусом оптической системы. Плоскость FF, проходящая через передний фокус F и перпендикулярная оптической оси называется передней фокальной плоскостью. Изображения предметов, находящихся в передней фокальной плоскости, получаются в бесконечности. Рассмотрим две сопряженные плоскости, перпендикулярные оптической оси системы. Отрезок прямой
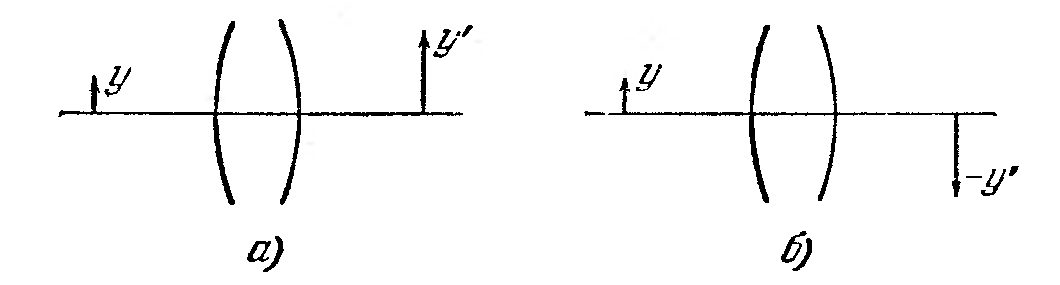
Размер прямого изображения считается положительным (
Рис.4. К определению линейного увеличения Отношение линейных размеров изображения к линейным размерам предмета называется линейным увеличением
Линейное увеличение – алгебраическая величина. Оно положительно, если изображение прямое ( Можно показать, что существуют такие сопряженные плоскости, которые отображаются друг в друга с увеличением Расстояние от передней главной точки Н до переднего фокуса F называется передним фокусным расстоянием
Рис. 5. Оптическая система Фокусные расстояния связаны соотношением:
где В случае, когда показатели преломления сред, находящихся по обе стороны от оптической системы, одинаковы, фокусные расстояния отличаются только знаком:
Если Фокальные и главные плоскости называются кардинальными плоскостями оптической системы. Фокусы и главные точки называются кардинальными точками оптической системы. Знание кардинальных плоскостей (или кардинальных точек) полностью определяет свойства оптической системы, в частности, дает возможность построить изображение, даваемое системой (см. рис.). На рис.
Можно показать, что справедлива формула Ньютона:
При
Линейное увеличение не зависит от размера предмета
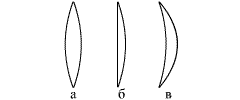
поэтому изображение плоского предмета, перпендикулярного оптической оси, будет подобно предмету. Изображение предмета, протяженного вдоль оптической оси, не подобно предмету. Это вытекает из зависимости линейного увеличения от Линзы Прозрачное тело, ограниченное сферическими поверхностями называется линзой. Виды линз. Линза может быть ограничена двумя выпуклыми сферическими поверхностями (двояковыпуклая линза - рис.6, а), выпуклой сферической поверхностью и плоскостью (плоско-выпуклая линза - рис.6, б), выпуклой и вогнутой сферическими поверхностями (вогнуто-выпуклая линза - рис. 6, в). Эти линзы посередине толще, чем у краев, и все они называются выпуклыми:
Рис.6.
Рис.7.
Тонкая линза
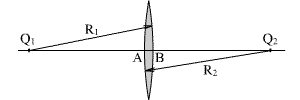
Мы будем рассматривать наиболее простой случай, когда толщина линзы l =|AB| пренебрежимо мала по сравнению с радиусами R1 и R2 поверхностей линзы и расстоянием предмета от линзы.
Рис.8.
Такую линзу называют тонкой линзой. В дальнейшем, говоря о линзе, будет подразумеваться именно тонкая линза. Точки А и B в тонкой линзе расположены столь близко друг к другу, что их можно принять за одну точку, которую называют оптическим центром линзы и обозначают точкой О. Луч света, проходящий через оптический центр линзы, практически не преломляется. Прямую О1О2, проходящую через центры сферических поверхностей, которые ограничивают линзу, называют ее главной оптической осью. Главная оптическая ось тонкой линзы проходит через оптический центр. Любую другую прямую, проходящую через оптический центр, называют побочной оптической осью. Изображение в линзах.
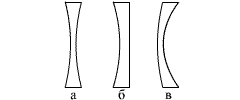
Рассеивающая линза. Подобно плоскому зеркалу линза создает изображения источников света. Это означает, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в одну точку (изображение), независимо от того, через какую часть линзы прошли лучи. Если по выходе из линзы лучи сходятся, они образуют действительное изображение. В случае же, когда прошедшие через линзу лучи являются расходящимися, пересекаются в одной точке не сами лучи, а их продолжения. Изображение тогда мнимое. Его можно наблюдать глазом непосредственно или с помощью оптических приборов. Собирающая линза. Точка, в которой пересекаются после преломлений в собирающей линзе лучи, падающие на линзу параллельноглавной оптической оси, называется главным фокусом линзы. Эту точку обозначают буквой F. Пустим три параллельных луча под углом к главной оптической оси. Мы увидим тогда, что пересечение произойдет не в главном фокусе линзы, а в другой точке. Точки пересечения лучей, падающих на линзу параллельными пучками, и при различных углах, образуемых этими пучками с главной оптической осью, располагаются в плоскости, перпендикулярной главной оптической оси и проходящей через главный фокус. Вогнутые линзы являются рассеивающими. Преломленные лучи будут расходящимися, а их продолжения пересекаются в главном фокусе рассеивающей линзы. В этом случае главный фокус является мнимым, и находиться на расстоянии F от линзы Порядок выполнения работы Юстировка Перед началом измерений центры всех линз нужно установить на одной высоте (юстировка по вертикали) и сделать оптические оси линз параллельными ребру оптической скамьи (юстировка по горизонтали). Юстировку проводят следующим путем. В окошко осветителя вставляют миру №5. Вплотную к осветителю пододвигают экран, на нем напротив центра миры делают отметку. Затем экран отодвигают к противоположному концу скамьи и между ним и осветителем помещают одну из собирающих линз. Передвигая линзу, получают на экране изображение миры. Перемещают линзу по высоте так, чтобы изображение центра миры на экране получалось на той же высоте, что и отметка. Вращая винт, перемещающий линзу в горизонтальном направлении, добиваются, чтобы изображение центра миры совпало с отметкой. Таким образом, последовательно юстируют все положительные линзы: коллиматорную линзу, линзы L1 и L2. Юстировку рассеивающей линзы L3 производят следующим образом. Между осветителем и экраном помещают уже юстированную собирающую линзу и рассеивающую линзу, подлежащую юстировке. Перемещая линзы, получают четкое изображение миры на экране. Перемещая центр отрицательной линзы по вертикали и горизонтали, добиваются совпадения центра изображения с отметкой на экране. Порядок выполнения работы Юстировка Перед началом измерений центры всех линз нужно установить на одной высоте (юстировка по вертикали) и сделать оптические оси линз параллельными ребру оптической скамьи (юстировка по горизонтали). Юстировку проводят следующим путем. В окошко осветителя вставляют миру №5. Вплотную к осветителю пододвигают экран, на нем напротив центра миры делают отметку. Затем экран отодвигают к противоположному концу скамьи и между ним и осветителем помещают одну из собирающих линз. Передвигая линзу, получают на экране изображение миры. Перемещают линзу по высоте так, чтобы изображение центра миры на экране получалось на той же высоте, что и отметка. Вращая винт, перемещающий линзу в горизонтальном направлении, добиваются, чтобы изображение центра миры совпало с отметкой. Таким образом, последовательно юстируют все положительные линзы: коллиматорную линзу, линзы L1 и L2. Юстировку рассеивающей линзы L3 производят следующим образом. Между осветителем и экраном помещают уже юстированную собирающую линзу и рассеивающую линзу, подлежащую юстировке. Перемещая линзы, получают четкое изображение миры на экране. Перемещая центр отрицательной линзы по вертикали и горизонтали, добиваются совпадения центра изображения с отметкой на экране. МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования ОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Им. Ф.М. ДОСТОЕВСКОГО Геометрическая оптика Учебно-методическое пособие по курсам «Оптика» и «Общий физический практикум» Омск 2019 Рецензенты:
К.ф.-м.н. Н.А. Давлеткильдеев (КНИОРП ОНЦ СО РАН) К.ф.-м.н., Г.М. Серопян (ФГБОУ ВО ОмГУ им. Ф.М. Достоевского)
Геометрическая оптика: учебно-методическое пособие по курсам «Оптика и «Общий физический практикум»/ авт.: Б.Т. Байсова, Л.В. Баранова.– Омск: изд-во Ом.гос.ун-та, 2019.–29 с.
В пособии представлены краткие теоретические сведения по разделу волновой оптики «Геометрическая оптика», обеспечивающие выполнение цикла лабораторных работ. Пособие также включает в себя лабораторный практикум и представляет собой самостоятельное руководство к лабораторным занятиям для студентов физического факультета. Практикум содержит описание выполнение лабораторных работ по курсам «Оптика» и «Общий физический практикум». Предназначено для обучающихся по направлениям подготовки бакалавров 03.03.02 «Физика», 03.03.03 «Радиофизика».
ОГЛАВЛЕНИЕ ПРЕДИСЛОВИЕ……………………………………………………………………4 ГЛАВА 1. Основные теоретические сведения……………………...…………..5 1. Законы распространения света …..………………………………..….…5 1.1. Закон независимости световых пучков …………...………………..5 1.2. Закон независимости световых пучков ….…………………...…….5 1.3. Закон отражения света ….……………………………………………5 1.4. Закон преломления света………………………………..………….....6 2. Зеркальное и диффузное отражение ……………………………………….. 7 3. Характеристики центрированной оптической системы………………….. 7 4. Линзы …………………………………………………………………………...12 4.1. Виды линз………………………………………………………….…….12 4.2. Тонкая линза……………………………………………………………..12 4.3. Изображение в линзах…………………………………………………..13 5. Зрительные трубы. Разрешающая способность зрительных труб………13 ГЛАВА 2. Лабораторный практикум…………..……………………………....17 2.1. Измерение фокусных расстояний тонких и толстых линз ….………….....17 2.2. Моделирование зрительных труб ………………………………………..26 СПИСОК ИСПОЛЬЗОВАННОЙ И РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ………………………………………………..………………..…29 ПРЕДИСЛОВИЕ Целью настоящего учебно-методического пособия является ознакомление студентов с основными теоретическими сведениями по теме «Геометрическая оптика» с последующим закреплением теории на практике при выполнении лабораторных работ. Пособие способствует формированию у студентов практических навыков работы на оптическом оборудовании с возможностью наглядного наблюдения изучаемых явлений с последующим оформлением результатов эксперимента. В первой главе изложены краткие теоретические сведения. В представленном теоретическом материале рассмотрены основные законы распространения света, способы получения когерентных волн в оптике, расчет интерференционной картины, интерференция в тонких пленках. Во второй главе представлен лабораторный практикум, включающий пять работ: «Определение длины световой волны с помощью колец Ньютона», «Определение длины световой волны с помощью бипризмы Френеля», «Определение толщины пластинки с помощью наблюдения интерференционных полос равного наклона», «Измерение показателей преломления жидкостей с помощью интерферометра Релея», «Изучение интерференции поляризованных лучей». По каждой работе представлены методические указания о порядке ее выполнения, описание лабораторных установок, а также перечень контрольных вопросов и список рекомендуемой литературы. Геометрическая оптика Геометрическая оптика – это раздел оптики, в котором изучаются законы распространения световой энергии в прозрачных средах на основе представления о световом луче. Световой луч – это линия, имеющая направление, вдоль которого распространяется энергия световых волн. В основу формального построения геометрической оптики положено четыре закона, установленных опытным путем:· закон прямолинейного распространения света;· закон независимости световых лучей;· закон отражения;· закон преломления света. В однородной среде свет распространяется прямолинейно, а на границе раздела сред с разными показателями преломления происходят явления отражения и преломления.
Законы распространения света 1.1. Закон прямолинейного распространения света: в оптически однородной среде (в частности, в вакууме) лучи света распространяются прямолинейно. Прямолинейностью распространения света объясняется образование тени, т.е. области, куда не поступает световая энергия. При малых размерах источника (светящаяся точка) получается резко очерченная тень. При больших размерах источника создаются нерезкие тени. Дело в том, что от каждой точки источника свет распространяется прямолинейно и предмет, освещенный уже двумя светящимися точками, даст две несовпадающие тени, наложение которых образует тень неравномерной густоты. Полная тень при протяженном источнике образуется лишь в тех участках экрана, куда свет не попадает совсем. По краям полной тени располагается более светлая область. Это полутень. 1.2. Закон независимости световых пучков: энергия в каждом пучке распространяется независимо от других пучков; освещенность поверхности, на которую падает несколько пучков, равна сумме освещенностей, создаваемых каждым пучком в отдельности. Закон отражения света. Луч света в однородной среде прямолинеен до тех пор, пока он не дойдет до границы этой среды с другой средой. На границе двух сред луч меняет свое направление. Часть света (а в ряде случаев и весь свет) возвращается в первую среду. Это явление называется отражением света. Одновременно свет частично проходит во вторую среду, меняя при этом направление своего распространения - преломляется.
Рис. 1. К закону отражения и преломления
Закон отражения света: Луч падающий 1, луч отраженный 2 и перпендикуляр, восстановленный в точке падения (т. О) к границе двух сред, лежат в одной плоскости. Угол падения α равен углу отражения β: α = β (1)
Закон преломления света. Луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред:
где n12 – относительный показатель преломления второй среды относительно первой. Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления n12 = n2/ n1. Абсолютным показателем преломления среды наз. величина n, равная отношению скорости с электромагнитных волн в вакууме к их фазовой скорости V в среде: n = с / V (3) Среда с большим оптическим показателем преломления называется оптически более плотной. Из симметрии выражения (1) вытекает обратимость световых лучей, сущность которой состоит в том, что если направить световой луч из второй среды в первую под углом β, то преломленный луч в первой среде выйдет под углом α. При переходе света из оптически менее плотной среды в более плотную получается, что sin α > sin β, т.е. угол преломления меньше угла падения света, и наоборот. В последнем случае при увеличении угла падения угол преломления увеличивается в большей мере, так что при некотором предельном угле падения α пр угол преломления становится равным π/2. С помощью закона преломления можно рассчитать значение предельного угла падения: sin α пр/sin(π/2) = n2/n1, откуда α пр = arcsin n2/n1. (4)
В этом предельном случае преломленный луч скользит по границе раздела сред. При углах падения α > α пр свет не проникает в глубь оптически менее плотной среды, имеет место явление полного внутреннего отражения. Угол α пр называется предельным угломполного внутреннего отражения. Явление полного внутреннего отраженияиспользуется в призмах полного отражения, которые применяются в оптических приборах: биноклях, перископах, рефрактометрах (приборах, позволяющих определять оптические показатели преломления), в световодах, представляющих собой тонкие, гнущиеся нити (волокна) из оптически прозрачного материала. Свет, падающий на торец световода под углами, большими предельного, претерпевает на границе раздела сердцевины и оболочки полное внутреннее отражение и распространяется только по световедущей жиле. С помощью световодов можно как угодно искривлять путь светового пучка.
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 95; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.88.132 (0.012 с.) |

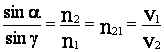 (2)
(2)
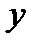 (рис.4), лежащий в одной из этих плоскостей, будет иметь своим изображением отрезок прямой
(рис.4), лежащий в одной из этих плоскостей, будет иметь своим изображением отрезок прямой 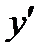 (рис.4,а), лежащий во второй плоскости. Изображение
(рис.4,а), лежащий во второй плоскости. Изображение 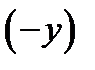 и
и 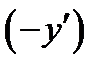 .
.
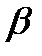 :
: (5)
(5)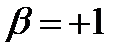 . Такие плоскости называются главными плоскостями оптической системы. Точки их пересечения с оптической осью называются главными точками системы. На рис. 5 главные плоскости обозначены НН и Н'Н'. НН называется передней главной плоскостью, Н'Н' – задней главной плоскостью.
. Такие плоскости называются главными плоскостями оптической системы. Точки их пересечения с оптической осью называются главными точками системы. На рис. 5 главные плоскости обозначены НН и Н'Н'. НН называется передней главной плоскостью, Н'Н' – задней главной плоскостью.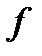 . Расстояние от задней главной точки Н' до заднего фокуса F' называется задним фокусным расстоянием
. Расстояние от задней главной точки Н' до заднего фокуса F' называется задним фокусным расстоянием 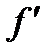 . Фокусные расстояния – алгебраические величины. Они положительны, если данный фокус лежит справа от соответствующей главной плоскости, и отрицательны в противном случае. Так, например, для системы, изображенной на рис.
. Фокусные расстояния – алгебраические величины. Они положительны, если данный фокус лежит справа от соответствующей главной плоскости, и отрицательны в противном случае. Так, например, для системы, изображенной на рис. 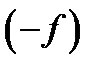 .
.
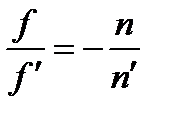 , (6)
, (6)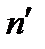 – показатель преломления среды, находящейся за оптической системой, а
– показатель преломления среды, находящейся за оптической системой, а 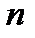 – показатель преломления среды, находящейся перед оптической системой.
– показатель преломления среды, находящейся перед оптической системой. 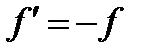 (7)
(7)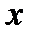 и
и 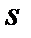 –расстояния от предмета до переднего фокуса и передней главной точки соответственно;
–расстояния от предмета до переднего фокуса и передней главной точки соответственно; 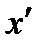 и
и 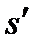 – расстояния от изображения до заднего фокуса и задней главной точки соответственно.
– расстояния от изображения до заднего фокуса и задней главной точки соответственно. 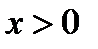 , если предмет расположен справа от переднего фокуса,
, если предмет расположен справа от переднего фокуса, 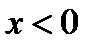 , если предмет расположен слева от переднего фокуса.
, если предмет расположен слева от переднего фокуса. 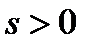 , если предмет расположен справа от передней главной точки,
, если предмет расположен справа от передней главной точки, 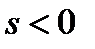 , если предмет расположен слева от передней главной точки.
, если предмет расположен слева от передней главной точки. 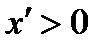 , если изображение расположено справа от заднего фокуса,
, если изображение расположено справа от заднего фокуса, 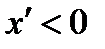 , если изображение расположено слева от заднего фокуса.
, если изображение расположено слева от заднего фокуса. 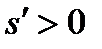 , если изображение расположено справа от задней главной точки,
, если изображение расположено справа от задней главной точки, 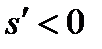 , если изображение расположено слева от задней главной точки.
, если изображение расположено слева от задней главной точки. или
или 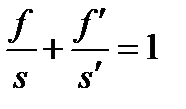 (8)
(8)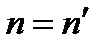 формулы (8) упрощаются следующим образом:
формулы (8) упрощаются следующим образом: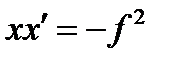 ,
, 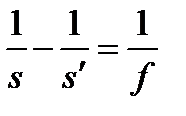 (9)
(9) :
: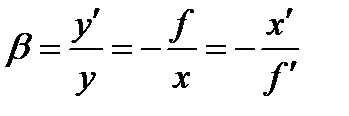 , (10)
, (10) .
.