
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Понятия необходимые для решения задач с помощью производнойСтр 1 из 4Следующая ⇒
Оглавление
Введение Глава 1. Понятия необходимые для решения задач с помощью производной Определение производной Предел функции Понятие интеграла Понятие дифференциала функции Глава 2. Применение производной к решению задач Исследование функции Применение производной при решении задач в разных науках Задачи по геометрии По аналитической геометрии По дифференциальной геометрии Задачи по физике Вычисление интегралов Доказательство неравенств Вычисление пределов (Правило Лопиталя) Заключение Список литературы производная интеграл функция неравенство предел
Введение Рассматриваемая тема является одним из разделов курса алгебры и начала анализа. Она имеет широкое применение в таких науках как физика, геометрия и др. Математический аппарат этой темы помогает при вычислении определенных и неопределенных интегралов и пределов функций, при доказательстве неравенств, помогает в исследовании функций в высшей математике. Кроме того, данная тема имеет свою историю, ей занимались и занимаются такие ученые как Г. Лейбниц, Ж. Лагранж, И. Ньютон, Г. Галилея, Р. Декарта. Подробнее остановимся на изложении исторического аспекта темы. Термин «производная» является буквальным переводом на русский французкого слова derive, которое ввел в 1797 г. Ж. Лагранж (1736-1813); он же ввел современные обозначения Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце XVII столетия. Тем более поразительно, что за долго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, но и сумел найти максимум функции Эта тема интересна и мне. Цель моей работы - расширить свой кругозор и научиться решать задачи по данной теме. Чтобы достигнуть цели, мне пришлось решить следующие исследовательские задачи.
. Подобрать и изучить материал по этой теме. . Из изученного материала выбрать главное. . Систематизировать основной материал в форме реферативно-поисковой работы. . Научиться решать задачи по теме. . Составить свои задачи по данной теме и решить их. . Подобрать и разработать наглядно-иллюстративный материал по данной теме.
Определение производной
Пусть мы имеем функцию y = f (x), (1)
определенную в некотором промежутке. При каждом значении аргумента x из этого промежутка функция y = f (x) имеет определенное значение. Пусть аргумент x получил некоторое (положительное или отрицательное- безразлично) приращение Δ x. Тогда функция y получит некоторое приращение Δ y. Таким образом: при значении аргумента x будем иметь y = f (x), при значении аргумента x + Δ x будем иметь y +Δ y = f (x + Δ x). Найдем приращение функции Δ y:
Δ y = f (x + Δ x)- f (x) (2)
Составим отношение приращения функции к приращению аргумента:
Найдем предел этого отношения при
или
Определение 1. Производной данной функции y = f (x) по аргументу x называется предел отношения приращения функции Δ y к приращению аргумента Δ x, когда последнее произвольным образом стремится к нулю. [5, с. 65] Заметим, что в общем случае для каждого значения x производная Наряду с обозначением
Конкретное значение производной при Пример 1. Дана функция 1) в произвольной точке x, 2) при Решение. 1) При значении аргумента, равном x, имеем Находим приращение функции
Составляем отношение
Переходя к пределу, найдем производную от данной функции:
Итак, производная от функции
) При
Пример 2. Решение. Рассуждая так же как в предыдущем примере, получаем:
Геометрический смысл производной. Теперь дадим не менее важное геометрическое истолкование производной. Для этого нам прежде всего потребуется определение касательной к кривой в данной точке.
Рис. 1. Рис. 2.
Пусть имеем кривую и на ней фиксированную точку Если при неограниченном приближении точки Определение 2. Прямая заданная уравнением
называется касательной к графику функции Рассмотрим функцию
В прямоугольной системе координат (рис. 2). При некотором значении
Если теперь
Следовательно,
т.е. значение производной Предел функции
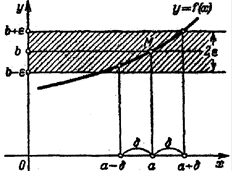
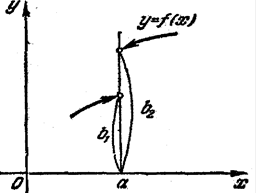
Определение 3. Пусть функция y = f (x) определена в некоторой окрестности точки a или в некоторых точках этой окрестности. Функция y = f (x) стремится к пределу b (y
Рис. 3.
Если b есть предел функции y = f (x) при
или Если Замечание. Предел функции f (x) при Пусть переменная величина x принимает значение так (упорядочена так), что если
то
то Другими словами, из двух точек числовой прямой последующей является та точка, которая ближе к точке a; при равных расстояниях последующая- та, которая правее от точки a.
Пусть упорядоченная таким образом переменная величина x стремится к пределу Рассмотрим, далее, переменную величину y = f (x). При этом будем считать, что из двух значений функции последующем является то значение, которое соответствует последующему значению аргумента. Если определенная так переменная величина y при
и говорить, что функция y = f (x) стремится к пределу b при
Рис. 4.
Замечание. Если f (x) стремится к пределу b Если x принимает только значения большие, чем a, то пишут Можно доказать, что если предел справа и предел слева существуют и равны, т.е. Пример 3. Докажем, что
Необходимо выполнение следующих неравенств:
Таким образом, при любом Замечание. Для существования предела функции при Пример 4. Докажем, что Нужно доказать, что при произвольном
если
или
Таким образом, при произвольном Определение 4. Функция
Зная смысл символов « « Которые символически записываются так:
Понятие интеграла
Пусть Разобьем отрезок
Обозначим длину отрезка Тогда величина
называется мелкостью разбиения. Зафиксируем произвольным образом точки и составим сумму
Суммы вида (11) называются интегральными суммами Римана. Определение 5. Функция
где
Если выполнены все условия определения 3, то число
Таким образом,
где или подробно
Определение 6. Число
где Если
(формула Ньютона-Лейбница). Запишем формулу Ньютона-Лейбница в следующем виде
где Теорема 1. (Основная теорема интегрального исчисления). Пусть
Доказательство: Положим
то есть
При Таким образом
Полагая здесь Теорема доказана. Исследование функции
Дифференциальное исчисление широко используется при исследовании функций. С помощью производной можно найти промежутки монотонности функции, ее экстремальные точки, наибольшие и наименьшие значения. Возрастание и убывание функций. Как известно функция, заданная на множестве
Если
то функция Аналогично определяются понятия убывающей и невозрастающей функций. Теорема 3. Если функция Доказательство. Рассмотрим две любые точки
где точка Поскольку оба множителя правой части равенства (18) положительны (
а значит, и
Итак,
Теорема 4. Если функция Доказательство этой теоремы аналогично. Пример 6. Докажем, что функция Решение. Имеем
Так как при любом Определение 7. Пусть функция то Точки максимума называют точками экстремума. [2, c. 85] Определение 8. Точки, в которых производная равна нулю или не существует, называют критическими (иногда точки, где производная равна нулю, называют стационарными). [2, c. 86] Теорема 5. пусть функция Если на Доказательство. Пусть производная По условию функция Таким образом, в
Это означает, что Рассмотрим случай, когда производная не меняет знака при переходе через точку Остальные два случая рассматриваются аналогично. Теорема доказана. [2, c. 101] Таким образом, чтобы исследовать функцию Пример 7. Исследуем на экстремум функцию Решение. Имеем
Приравняв производную к нулю, находим
Задачи по геометрии
По аналитической геометрии Пример 8. Найти угол между касательной к графику функции Решение. Найдем угловой коэффициент касательной к кривой Производная функции Пример 9. Найти уравнение касательной к графику функции Решение. Значение функции
Пример 10. Доказать, что касательная к параболе Решение. Пусть
Найдем точку пересечения этой касательной с осью абсцисс. Из равенства Пример 11. Найти тангенсы углов наклона касательной к кривой Решение. Имеем
Задачи по физике
Пусть точка движется вдоль некоторой прямой. Выберем на прямой начало отсчета, положительное направление и единицу измерения. Тогда положение точки на прямой будет определяться ее координатой. Зависимость
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 94; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.213.209 (0.198 с.) |
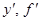 . Такое название отражает смысл понятия: функция
. Такое название отражает смысл понятия: функция 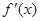 происходит из
происходит из 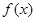 , является производным от
, является производным от 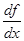 . Символ
. Символ 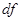 Лейбниц выбрал для обозначения дифференциала функции
Лейбниц выбрал для обозначения дифференциала функции 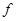 .
.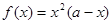 . В XVII в. на основе учения Г. Галилея о движении активно развивалась кинематическая концепция производной.
. В XVII в. на основе учения Г. Галилея о движении активно развивалась кинематическая концепция производной.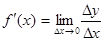
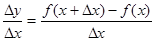 . (3)
. (3)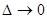 . Если этот предел существует, то его называют производной данной функции f (x) и обозначают
. Если этот предел существует, то его называют производной данной функции f (x) и обозначают 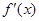 . Таким образом, по определению,
. Таким образом, по определению,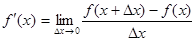 . (4)
. (4)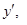
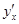 ,
, 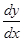 .
.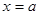 обозначается
обозначается 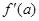 или
или  . Операция нахождения производной от функции f (x) называется дифференцированием этой функции.
. Операция нахождения производной от функции f (x) называется дифференцированием этой функции.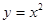 ; найти ее производную
; найти ее производную 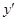 :
: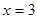 .
.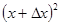 .
.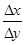 :
: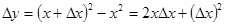 .
.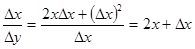 .
.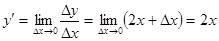 .
.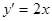 .
.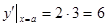 .
.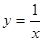 ; найти
; найти 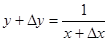 ;
;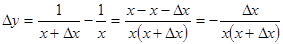 ;
;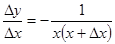 ;
; 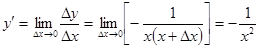 .
.
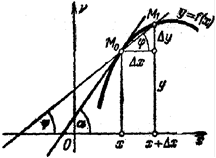
 . Возьмем на кривой точку
. Возьмем на кривой точку  и проведем секущую
и проведем секущую  (рис. 1). Если точка
(рис. 1). Если точка 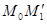 ,
, 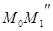 и т. д.
и т. д.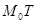 , то эта прямая называется касательной к кривой в точке
, то эта прямая называется касательной к кривой в точке 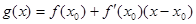
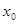 . [6, c. 134]
. [6, c. 134]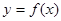
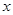 функция имеет значение
функция имеет значение 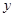 на кривой соответствует точка
на кривой соответствует точка 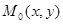 . Дадим аргументу
. Дадим аргументу 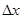 . Новому значению аргумента
. Новому значению аргумента 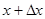 соответствует «наращенное» значение функции
соответствует «наращенное» значение функции 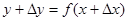 . Соответствующей ему точкой кривой будет точка
. Соответствующей ему точкой кривой будет точка 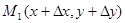 . Проведем секущую
. Проведем секущую 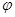 угол, образованный секущей с положительным направлением оси
угол, образованный секущей с положительным направлением оси 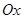 . Составим отношение
. Составим отношение 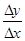 . Из рисунка 1 непосредственно усматриваем, что
. Из рисунка 1 непосредственно усматриваем, что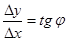 . (5)
. (5)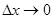 угол
угол 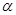 , то прямая, проходящая через
, то прямая, проходящая через 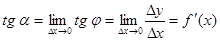 .
.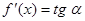 , (6)
, (6)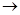 b) при x, стремящемся к a
b) при x, стремящемся к a 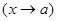 , если для каждого положительного числа
, если для каждого положительного числа 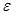 , как бы мало оно ни было, можно указать такое положительное число
, как бы мало оно ни было, можно указать такое положительное число 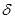 , что для всех x, отличных от a и удовлетворяющих неравенству
, что для всех x, отличных от a и удовлетворяющих неравенству 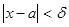 , имеет место неравенство
, имеет место неравенство 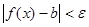 .
.
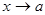 , то пишут:
, то пишут: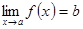
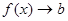 при
при 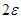 , ограниченной прямыми
, ограниченной прямыми 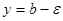 и
и 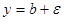 . [5, c. 31]
. [5, c. 31]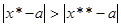 ,
,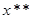 есть последующее, а
есть последующее, а 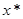 - предыдущее значение; если же
- предыдущее значение; если же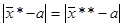 и
и 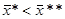 ,
,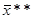 есть последующее, а
есть последующее, а 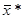 - предыдущее.
- предыдущее.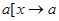 или
или 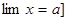 .
.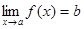
 при x, стремящемся к некоторому числу a так, что x принимает только значения, меньшие a, то пишут
при x, стремящемся к некоторому числу a так, что x принимает только значения, меньшие a, то пишут 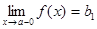 и называют
и называют 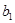 пределом функции в точке a справа (рис.4).
пределом функции в точке a справа (рис.4).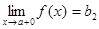 и называют
и называют 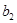 пределом функции в точке a справа (рис.4).
пределом функции в точке a справа (рис.4).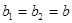 , то
, то 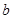 и будет пределом в смысле данного выше определения предела в точке a. И обратно, если существует предел функции b в точке a, то существуют пределы функции в точке a справа и слева и они равны.
и будет пределом в смысле данного выше определения предела в точке a. И обратно, если существует предел функции b в точке a, то существуют пределы функции в точке a справа и слева и они равны.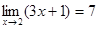 . Действительно, пусть задано произвольное
. Действительно, пусть задано произвольное 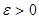 ; для того чтобы выполнялось неравенство
; для того чтобы выполнялось неравенство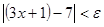 ,
,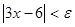 ,
, 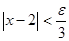 ,
, 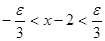 .
.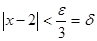 , значение функции
, значение функции 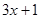 будет отличаться от 7 меньше чем на
будет отличаться от 7 меньше чем на 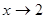 .
.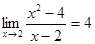 . Здесь функция
. Здесь функция 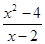 не определена при
не определена при  .
.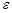 найдется такое
найдется такое 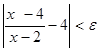 , (7)
, (7)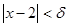 . Но при
. Но при 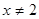 неравенство (7) эквивалентно неравенству
неравенство (7) эквивалентно неравенству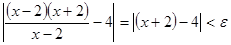
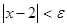 . (8)
. (8)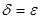 ). А это и значит, что данная функция при
). А это и значит, что данная функция при 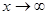 , если для каждого произвольно малого положительного числа
, если для каждого произвольно малого положительного числа 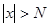 , будет выполняться неравенство
, будет выполняться неравенство 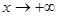 ,
, 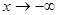 , очевидным является и смысл выражений:
, очевидным является и смысл выражений: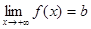 ,
, 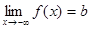 .
.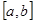 , где
, где 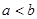
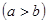 , и
, и 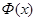 - некоторая первообразная при
- некоторая первообразная при 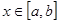 .
.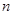 частей
частей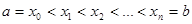 . (9)
. (9)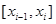 ,
, 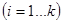 через
через 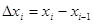 .
.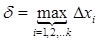 (10)
(10)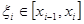 ,
, 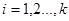
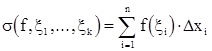 (11)
(11)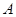 , что любой последовательности разбиений отрезка
, что любой последовательности разбиений отрезка 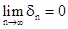 и для любого выбора точки xiÎ
и для любого выбора точки xiÎ  выполняется равенство
выполняется равенство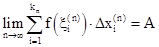 , (12)
, (12)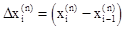
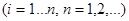 . [8, c. 54]
. [8, c. 54]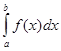 . (13)
. (13)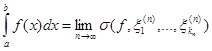 ,
,
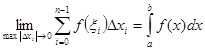 (14)
(14)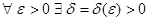 : для любого разбиения
: для любого разбиения 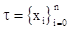
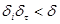 , каковы бы ни были точки
, каковы бы ни были точки 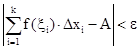
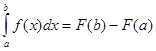
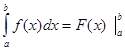 ,
,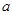 и
и 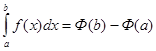 . (16)
. (16)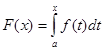 , но тогда
, но тогда 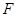 ,
, 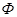 - две первообразные одной и той же функции
- две первообразные одной и той же функции 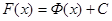 ,
, 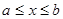 ,
,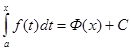 .
.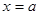 следует, что
следует, что  .
.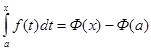 .
.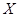 , называется возрастающей на этом множестве, если для любых
, называется возрастающей на этом множестве, если для любых 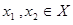 , таких, что
, таких, что 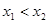 , имеем
, имеем 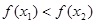 :
: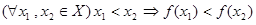 .
.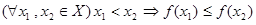 ,
, называется неубывающей на множестве
называется неубывающей на множестве 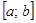 , а ее производная положительна на интервале
, а ее производная положительна на интервале 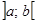 , то
, то 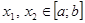 , такие, что
, такие, что 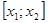 выполняется условие теоремы Лагранжа, то
выполняется условие теоремы Лагранжа, то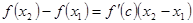 , (18)
, (18)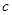 лежит между
лежит между 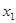 и
и 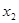 .
.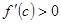 по условию,
по условию, 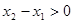 в силу выбора точек), то
в силу выбора точек), то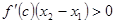 , (19)
, (19)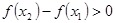 .
.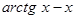 убывает на всей числовой прямой.
убывает на всей числовой прямой.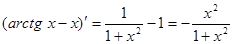 .
.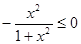 и, кроме того, равенство
и, кроме того, равенство 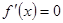 выполняется только в одной точке
выполняется только в одной точке 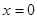 , то на всей числовой прямой
, то на всей числовой прямой 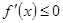 , причем
, причем 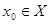 и непрерывна в этой точке. Если существует такая окрестность точки
и непрерывна в этой точке. Если существует такая окрестность точки 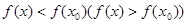 ,
,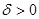 , такое, что функция
, такое, что функция 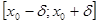 , дифференцируема на интервалах
, дифференцируема на интервалах 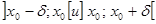 , причем производная данной функции сохраняет знак на каждом из этих интервалов.
, причем производная данной функции сохраняет знак на каждом из этих интервалов.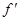 положительна на интервале
положительна на интервале 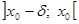 и отрицательна на
и отрицательна на 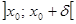 . Докажем, что
. Докажем, что 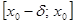 , дифференцируема в интервале
, дифференцируема в интервале 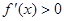 . Значит по теореме 1 функция
. Значит по теореме 1 функция 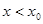 , где
, где 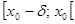 , следует
, следует 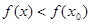 . Аналогично устанавливаем, что функция
. Аналогично устанавливаем, что функция 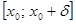 , а поэтому из неравенства
, а поэтому из неравенства 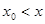 , где
, где 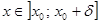 , следует
, следует 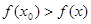 .
.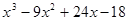 .
.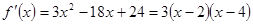 .
.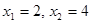 . При переходе через точку
. При переходе через точку 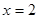 производная меняет знак с «+» на «-», значит, в этой точке функция имеет максимум. При переходе через точку
производная меняет знак с «+» на «-», значит, в этой точке функция имеет максимум. При переходе через точку 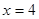 производная меняет знак с «-» на «+», значит, в этой точке функция имеет минимум. Имеем
производная меняет знак с «-» на «+», значит, в этой точке функция имеет минимум. Имеем 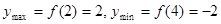 .
. в точке
в точке  и осью
и осью 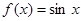 равна
равна 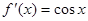 . По формуле
. По формуле 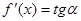 находим
находим 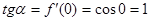 , откуда
, откуда 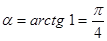 .
.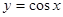 в точке с абсциссой
в точке с абсциссой 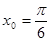 .
.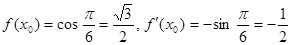 . Используя формулу
. Используя формулу 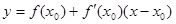 , найдем искомое уравнение касательной:
, найдем искомое уравнение касательной: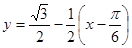 или
или 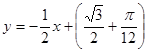 .
.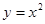 в точке с абсциссой
в точке с абсциссой 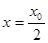 .
.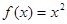 , тогда
, тогда 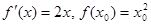 и
и 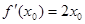 .По формулу
.По формулу 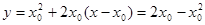 .
.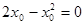 находим
находим 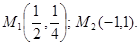
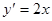 ; следовательно,
; следовательно,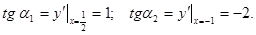
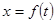 называется законом движения точки. Средней скоростью движения называют отношение перемещения к промежутку времени, в течение которого это пер
называется законом движения точки. Средней скоростью движения называют отношение перемещения к промежутку времени, в течение которого это пер


