
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение производной при решении задач в разных наукахСодержание книги
Поиск на нашем сайте
Задачи по геометрии
По аналитической геометрии Пример 8. Найти угол между касательной к графику функции Решение. Найдем угловой коэффициент касательной к кривой Производная функции Пример 9. Найти уравнение касательной к графику функции Решение. Значение функции
Пример 10. Доказать, что касательная к параболе Решение. Пусть
Найдем точку пересечения этой касательной с осью абсцисс. Из равенства Пример 11. Найти тангенсы углов наклона касательной к кривой Решение. Имеем
По дифференциальной геометрии Пример 12. Найти геодезическую кривизну винтовой линии
Решение. Запишем формулу для вычисления
Положим
Пример 13. Для кривой Решение. Проверим, лежит ли точка
Точка Напишем уравнение кривой в векторном виде: В точке Уравнение касательной в точке
Найдем уравнение бинормали, ее направляющий вектор коллинеарен вектору
Главная нормаль задается уравнением Пример 14. Найти длину дуги одного витка кривой:
Решение. Данная кривая пересекает плоскость Тогда
В промежутке
Задачи по физике
Пусть точка движется вдоль некоторой прямой. Выберем на прямой начало отсчета, положительное направление и единицу измерения. Тогда положение точки на прямой будет определяться ее координатой. Зависимость v ср =
или v ср =
Если положить v ср = Мгновенной скоростью в момент времени t называют предел средней скоростью движения за промежуток v мгн =
Так как Дифференциал координаты равен Решение. Закон свободного падения имеет вид Дадим аргументу приращение
Главная линейная часть приращения
I ср=
За силу тока I в момент времени
т.е. сила тока есть производная от количества электричества, как функции от времени. Пример 17. Пусть дан неоднородный стержень длины Решение. Если
т.е. линейная плотность стержня в данной точке есть производная массы стержня как функции от его длины. Рассмотренные примеры показывают, как используются производная для изучения скорости протекания неравномерных процессов. При этом само понятие скорости понимается в широком смысле. Например, плотность стержня есть скорость изменения массы части стержня как функции его длины. В общем случае можно сказать так: Вычисление интегралов
Интегрирование по частям. Пусть Интегрируя обе части тождества в пределах от
Так как
или окончательно
Пример 17. Вычислить интеграл Решение.
Доказательство неравенств
При доказательстве неравенств методами дифференциального исчисления используются теоремы о монотонности функций. Пример 18. Докажем, что для всех Решение. Составим вспомогательную функцию Так как при Значит, Таким образом, Пример 19. Докажем, что при
Решение. Составим вспомогательную функцию
и найдем ее производную
Из предыдущего примера следует, что
и, следовательно,
Что и требовалось доказать. Пример 20. Докажем, что если Решение. Исследуем на монотонность функцию
если
|
||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

 в точке
в точке 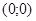 и осью
и осью 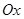 .
.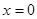 .
.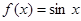 равна
равна 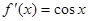 . По формуле
. По формуле 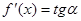 находим
находим 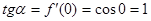 , откуда
, откуда 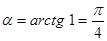 .
.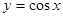 в точке с абсциссой
в точке с абсциссой 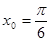 .
.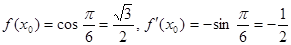 . Используя формулу
. Используя формулу 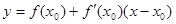 , найдем искомое уравнение касательной:
, найдем искомое уравнение касательной: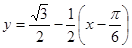 или
или 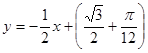 .
.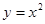 в точке с абсциссой
в точке с абсциссой 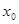 пересекает ось
пересекает ось 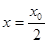 .
.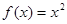 , тогда
, тогда 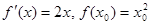 и
и 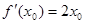 .По формулу
.По формулу 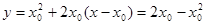 .
.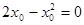 находим
находим 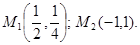
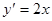 ; следовательно,
; следовательно,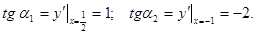
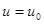 , лежащей на прямом геликоиде
, лежащей на прямом геликоиде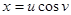 ,
, 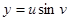 ,
, 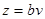 .
.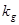 :
: .
.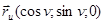 ,
, 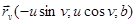 ,
,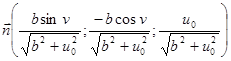 .
.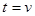 , тогда
, тогда 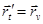 ,
, 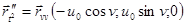 . Применяя формулу для вычисления
. Применяя формулу для вычисления 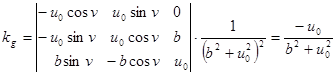 .
.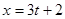 ,
, 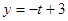 ,
, 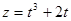 составить уравнение касательной, главной нормали, бинормали в точке
составить уравнение касательной, главной нормали, бинормали в точке 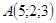 .
.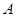 на кривой:
на кривой: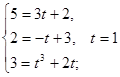 .
.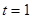 .
.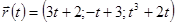 . Тогда
. Тогда 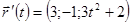 ,
, 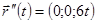 .
.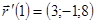 ,
, 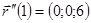 .
.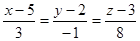 .
.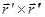 .
.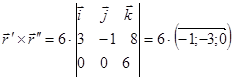 ,
,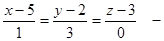 уравнение бинормали. Найдем направляющий вектор главной нормали:
уравнение бинормали. Найдем направляющий вектор главной нормали: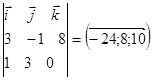 .
.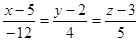 .
.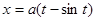 ,
, 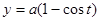 ,
, 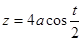 (где
(где 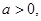
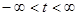 ) между двумя ее соседними точками пересечения с плоскостью
) между двумя ее соседними точками пересечения с плоскостью  .
.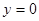 . Отсюда следует, что
. Отсюда следует, что 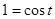 ;
; 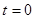 и
и 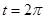 - значения параметра
- значения параметра 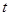 между двумя соседними точками пересечения с плоскостью
между двумя соседними точками пересечения с плоскостью 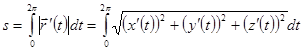 ,
,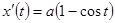 ,
, 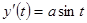 ,
, 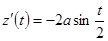 ,
,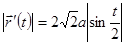 .
.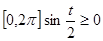 , поэтому
, поэтому  . Следовательно, длина дуги
. Следовательно, длина дуги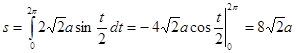 .
.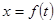 называется законом движения точки. Средней скоростью движения называют отношение перемещения к промежутку времени, в течение которого это перемещение произошло. Если, скажем, точка за промежуток времени от t 1 до t 2 прошла путь от А до В и вернулась обратно в А, то перемещение равно 0 и средняя скорость v ср равна 0. В общем случае имеем
называется законом движения точки. Средней скоростью движения называют отношение перемещения к промежутку времени, в течение которого это перемещение произошло. Если, скажем, точка за промежуток времени от t 1 до t 2 прошла путь от А до В и вернулась обратно в А, то перемещение равно 0 и средняя скорость v ср равна 0. В общем случае имеем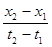 ,
,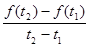 .
.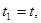
 , то средняя скорость за промежуток времени
, то средняя скорость за промежуток времени 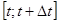 окажется равной:
окажется равной: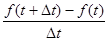 .
.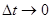 . Значит,
. Значит,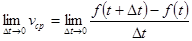 .
.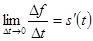 , то мгновенная скорость прямолинейно движущейся точки есть производная координаты (пути) x по времени t. в этом состоит механический смысл производной.
, то мгновенная скорость прямолинейно движущейся точки есть производная координаты (пути) x по времени t. в этом состоит механический смысл производной.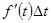 , т.е. v мгн
, т.е. v мгн 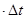 . Это путь, который прошло бы тело за промежуток времени
. Это путь, который прошло бы тело за промежуток времени 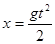 . Согласно сказанному выше v мгн =
. Согласно сказанному выше v мгн = 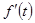 . Значит нужно найти производную функции
. Значит нужно найти производную функции 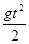 .
.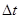 . Тогда
. Тогда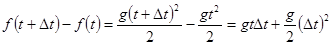 .
.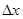 имеет вид
имеет вид 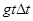 , а потому
, а потому 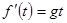 . Итак, v мгн =
. Итак, v мгн = 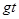 . Пример 16. Пусть
. Пример 16. Пусть 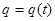 - количество электричества, протекающее через поперечное сечение проводника за время
- количество электричества, протекающее через поперечное сечение проводника за время 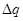 - количество электричества, протекающее через поперечное сечение проводника за время
- количество электричества, протекающее через поперечное сечение проводника за время 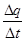 - средняя сила тока за промежуток времени
- средняя сила тока за промежуток времени 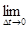 I ср. Таким образом,
I ср. Таким образом,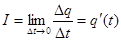 ,
,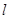 ,
, 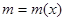 - масса части стержня длины
- масса части стержня длины 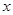 (один из концов стержня принимается за начало отсчета). Найдем линейную плотность стержня в данной точке
(один из концов стержня принимается за начало отсчета). Найдем линейную плотность стержня в данной точке 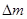 - масса части стержня между точками, расположенными соответственно на расстоянии
- масса части стержня между точками, расположенными соответственно на расстоянии 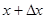 от начала отсчета, то
от начала отсчета, то 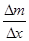 - средняя линейная плотность стержня на рассматриваемом участке, а
- средняя линейная плотность стержня на рассматриваемом участке, а 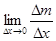 -искомая линейная плотность
-искомая линейная плотность 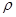 . Таким образом,
. Таким образом,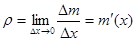 ,
,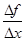 - средняя скорость изменения функции
- средняя скорость изменения функции 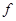 на отрезке
на отрезке 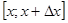 , а
, а 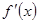 - скорость изменения
- скорость изменения 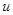 и
и 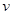 - дифференцируемые функции от
- дифференцируемые функции от 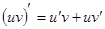 .
.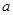 до
до 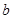 , получим:
, получим: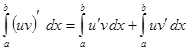 . (20)
. (20)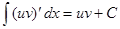 , то
, то 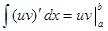 ; поэтому равенство (20) может быть записано в виде
; поэтому равенство (20) может быть записано в виде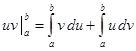 ,
,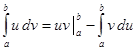 .
. .
.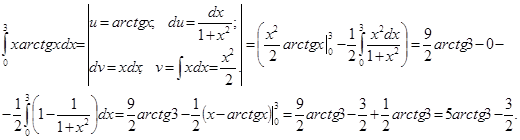

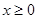 справедливо неравенство
справедливо неравенство 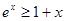 .
.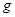 , где
, где 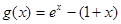 , и найдем ее производную
, и найдем ее производную 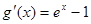 .
.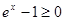 , причем равенство возможно лишь в случае
, причем равенство возможно лишь в случае 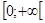 . В частности, выполняется неравенство
. В частности, выполняется неравенство 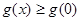 . Но
. Но 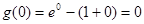 .
.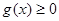 , т.е.
, т.е. 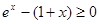 .
.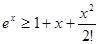 .
.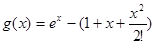 ,
,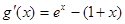 .
.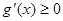 , значит, функция
, значит, функция 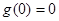 , то получаем
, то получаем 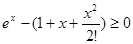
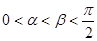 , то
, то 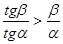 .
.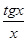 . Имеем
. Имеем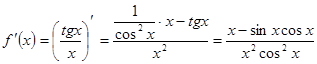 .
. , то, как известно,
, то, как известно, 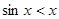 и тем более
и тем более 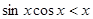 . Значит, в интервале
. Значит, в интервале 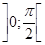 выполняется неравенство
выполняется неравенство 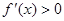 , а потому функция
, а потому функция 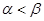 следует
следует 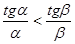 , т.е.
, т.е. 


