Классическая формула вероятности.

Событием называется всякий факт, который может произойти или не произойти в результате опыта. При этом тот или иной результат опыта может быть получен с различной степенью возможности.

Вероятностью события A называется математическая оценка возможности появления этого события в результате опыта. Вероятность события A равна отношению числа,

благоприятствующих событию A исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий.

P (A) = m

n

Исход опыта является благоприятствующим событию A, если появление в результате опыта этого исхода влечет за собой появление события A.

Значение вероятности любого события – есть положительное число, заключенное между нулем и единицей.

0 £ P (A) £ 1

Пример. Бросают игральную кость. Событие А – “четное число очков”. Определить вероятность этого события.

Решение. Событию А благоприятствуют грани кости со значениями «2», «4» и «6» - всего три исхода. Общее число исходов равно числу граней, то есть шесть. Применим

классическую формулу вероятности

P (A) = 3 = 0,5. Ответ:0,5

6

Планиметрия.

 

a, b – катеты, c – гипотенуза, a c, b c – проекции катетов на гипотенузу, h c – высота, опущенная на гипотенузу a 2 + b 2 = c 2 (теорема Пифагора) Площадь треугольника S = 1 ab S = 1 c × h S = 1 bc sin a 2        2 c               2

 

Для произвольного выпуклого четырехугольника (параллелограмм, трапеция),

диагонали которого равны площади:

d 1,

d 2, а угол между ними a, имеет место формула вычисления

S = 1 d d

sin a,

 

для ромба

2 1 2

S = 1 d d  ,

2 1  2

для трапеции с основаниями a, b и высотой h

S = a +  b h.

2

 

Стереометрия.

Для произвольной призмы объем вычисляется по формуле (S – площадь основания, H

– высота фигуры).

V = SH.

Для прямоугольного параллелепипеда (a, b, c –  ребра  параллелепипеда, d –

диагональ, S б

– площадь боковой поверхности) справедливы формулы:

б

V = abc, S = 2(a + b) c, a 2 + b 2 + c 2 = d 2.

Для правильной пирамиды (P – периметр основания, h – апофема, S б

боковой поверхности) используются формулы:

– площадь

 

1

S   = Ph, объем V

б       2

= SH.

1

3

Последняя формула также справедлива и для произвольной пирамиды. Для цилиндра и конуса используются формулы:

б

S = 2 p RH, V

б

S = p Rl, V

= p R 2  H

= 1  p R 2  H

3

(для цилиндра) (для конуса)

где R – радиус основания, H – высота, l – образующая конуса.

Для сферы радиуса R площадь поверхности определяется по формуле:

S = 4 p R 2 ,

а для шара радиуса R объем вычисляется по формуле:

V   = 4  p R 3 .

3

 

 

ДЕМОНСТРАЦИОННЫЕ ВАРИАНТЫ ЗАДАНИЙ БАЗОВОЙ ЧАСТИ

1. Простейшие текстовые задачи. Проценты, вычисления, округления.

ü Одноразовый билет на автобус для взрослого стоит 600 руб. Стоимость билета для учащегося составляет 50% стоимости билета для взрослого. Группа состоит из 10 учащихся и 4 взрослых. Сколько рублей затрачено на билеты для всей группы?

Решение. Стоимость билета учащегося находим как процент от числа 50% = 0.5,

тогда 600 × 0,5 = 300(руб). Тогда стоимость всех билетов учащихся  составляет

300×10 = 3000(руб). На билеты для взрослых  требуется  600 × 4 = 2400(руб).

Итого для всей группы затраты на билеты составят 3000 + 2400 = 5400(руб). Ответ:5400.

ü Блокнот стоит 30 рублей. Какое наибольшее число таких блокнотов можно будет купить на 650 рублей после понижения цены на 10%?

Решение. Снижение цены находим как процент от числа 10% = 0.1, что составляет

30 × 0,1 = 3(руб). Стоимость блокнота после снижения составляет 30 - 3 = 27(руб).

Найдем  количество  блокнотов  по  сниженной  цене,  которое  можно  купить  на  650

рублей 650: 27 = 24,07(руб). По смыслу задачи, число купленных блокнотов –

целое значение, поэтому округляем в меньшую сторону и получаем – 24 блокнота. Ответ: 24.

ü В разгар сезона 1 кг вишни стоил 80 рублей. В октябре вишни подорожали на 20%. Сколько килограмм (целых) вишни можно купить после подорожания на 770 рублей?

Решение. Повышение цены находим как процент от числа 20% = 0.2, что  составляет

80× 0,2 =16(руб).   Стоимость   вишни   после   повышения   составляет

80 +16 = 96(руб). Найдем количество килограммов по увеличенной цене, которое

можно купить на 770 рублей

770: 96 = 8,02(руб). По условию задачи, покупается

целое число килограммов вишни, поэтому округляем в меньшую сторону и получаем – 8 килограмм. Ответ: 8.

2.

7 - 6 x

Простейшие иррациональные уравнения.

ü Решить уравнение

= 7.

Решение. Возведем обе части уравнения в степень корня, в данном случае во вторую,

получим (

7 - 6 x)2 = 72. На основании свойств степени знак радикала «снимается»

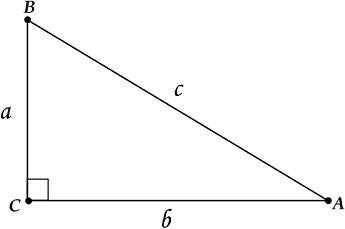
7 - 6 х = 49. Далее решается простейшее линейное уравнение - 6 х = 49 - 7,

умножим обе части уравнения на (-1), выражение примет вид

х = 6. Ответ: 6.

3. Преобразование алгебраических выражений и дробей.

ü Найдите значение выражения 56 ×38 :155

56 × 38

6 х = -42, в результате

Решение. По свойствам степени

Ответ: 135

55 × 35

= 56-1 × 38-5 = 51 ×33 = 5× 27 =135

ü Найти значение выражения 10⁴¹× 10⁴⁴:10⁸³

Решение.

Воспользуемся свойствами степени 1041+44-83 =1085-83 =102 =100. Ответ: 135.

4.
Решение прямоугольных треугольников с использованием тригонометрических функций.

ü В треугольнике ABC угол С равен 90°, АВ = 10, АС = 8. Найти sin В.

Решение. По определению sin B =

Ответ: 0,8

AC, значит sin B = 8

AB                  10

= 0,8

ü В треугольнике ABC угол С равен 90°, АС =5, ВС =6. Найти tg A.

Решение. По определению tgA = CB, значит tgA = 6 = 1,2

Ответ: 1,2

AC                5

ü В треугольнике ABC угол С равен 90°, sin A = 0,6. Найти cos A.

Решение.    Воспользуемся    основным    тригонометрическим    тождеством

1- sin 2 A

cos2   A + sin2   A = 1, следовательно, cos A =               подставим заданное значение

1- 0,36

0,64

cos A =          =      = 0,8.

Так как острые углы прямоугольного треугольника принадлежат первой четверти, то знаки их тригонометрических функций – положительные.

Ответ: 0,8

 

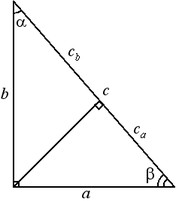
ü В треугольнике ABC угол С равен 90°, высота СН равна 6, АH =10. Найдите tg A.

 

Решение. По определению tgA = CH, значит tgA = 6 = 0,6 AH                10 Ответ: 0,6

 

 

5. Преобразование числовых логарифмических выражений.

При решении данного вида задач применим свойства логарифмов

ü Вычислить

log6 36 + log6 1 = 2 + 0 = 2. Ответ: 2

ü Вычислить: 8 × 6log6 2  = 8× 2 =16.          Ответ: 16

ü Вычислить: log 3

54 - log 3

2 = log 3

54 = log

2     3

27 = 3. Ответ: 3

 

ü Вычислить: log 5

3 + log 5

125

3

= log 5

3×125 = log 3   5

125 = 3. Ответ: 3

6. Задачи с прикладным содержанием. Алгебраические уравнения и неравенства.

ü Мотоциклист, движущийся по городу со скоростью

v 0 = 29км/ч, выезжает за

город и разгоняется с постоянным ускорением а = 4 км/ч². Расстояние до города

at 2

определяется по формуле

S = v 0 t +

. Найти наибольшее время (в минутах), в течение

2

которого мотоциклист будет находиться в зоне действия сотовой вышки, если оператор связи гарантирует покрытие не более 15 км от города.

Решение. Составим уравнение движения, используя условия задачи

4 t 2 +

2

29 t £ 15, получим квадратное неравенство

2 t 2

+ 29 t -15 £ 0. Найдем корни

соответствующего квадратного уравнения

t 1, 2

= - 29 ±

841- 8 × (-15)

, так как

4

 

время принимает  только  положительные значение

t = - 29 + 31 = 0,5час. Эта

4

величина и будет наибольшим значением времени, в течение которого мотоциклист будет находиться в зоне действия сотовой вышки. Переведем полученный результат в минуты 0,5 час = 30 мин.

Ответ: 30

 

ü Автомобиль,  движущийся  в  начальный  момент  времени  со скоростью

0

v = 7м/с, начинает тормозить с постоянным ускорением а = 1 м/с². За t секунд после начала

at 2

торможения, он проходит путь

S = v 0 t -

. Найти наименьшее время (в секундах), от

2

момента начала торможения, если автомобиль проехал не менее 20 метров.

Решение. Составим уравнение движения, используя условия задачи

t 2

20 £ 7 t -

, получим квадратное неравенство

2

- t 2 +14 t - 40 ³ 0. Найдем корни

 

соответствующего квадратного уравнения

t 1, 2 =

-14 ±

196 - 4 × 40

- 2

-14 ± 6

 

, так как время

принимает только положительные   значение

t 1, 2 =

- 2 Þ t 1 = 4, t 2 = 10.

Решением исходного неравенства будет множество значений:

4 £ t £ 10.

Наименьшим значением времени, от момента начала торможения будет значение 4. Ответ: 4.

ü Зависимость объема спроса q на продукцию предприятия-монополиста от

цены p (тыс. руб.) задается формулой:

q = 100 -10 p. Выручка предприятия за месяц n (тыс.

руб.) определяется как

n (p) = q × p. Определить наибольший уровень цены p (тыс. руб.), при

котором месячная выручка n(p) составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.

Решение. Составим уравнение для выручки предприятия, используя условия задачи

n (p) = (100 -10 p) × p = -10 p 2 +100 p,   получим  квадратное  неравенство

-10 p 2 +100 p £ 240. Упростим выражение  - p 2 +10 p - 24 £ 0. Найдем корни

 

соответствующего квадратного уравнения

p 1, 2

= -10 ±

100 - 4 × 24

- 2       , так как

уровень    цены    принимает    только    положительные             значение

t = -10 ± 2 Þ  p

 

= 4, p

= 6. Решением исходного неравенства будет множество

1, 2               - 2      1                    2

значений: 4 £ t £ 6. Наибольшим значением уровня цены p (тыс. руб.), при котором

месячная выручка n(p) составит не менее 240 тыс. руб. будет значение равное 6. Ответ: 6.