
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие IV . Квадратный трехчлен: теорема Виета; знаки корней квадратного трехчлена; соотношения на корни квадратного уравненияСодержание книги
Поиск на нашем сайте
Цель: закрепление умения использовать теорему Виета для определения знаков корней квадратного трехчлена и решения задач на соотношения между корнями квадратного уравнения; применение имеющихся знаний при решении задач; формирование умения работать в группе. Ход занятия: Организационный момент. 2. Проверка домашнего задания: 3 ученика до начала занятия записывают решение задач №1-3 на доске. На занятии учащиеся проверяют решение, исправляют ошибки. Задачи №4-6 учитель проверяет индивидуально у каждого учащегося. 3. Решение задач. Класс делится на группы по 4-5 человек. Каждая группа получает по 2 блока заданий (у всех задания одинаковые), которые необходимо решить за определенное время (20 мин). За каждое верно решенное задание первого блока будет ставиться 2 балла, второго блока – 3 балла. За 17 минут до окончания занятия группы прекращают свою работу, начинается проверка и обсуждение решений, найденных группами. По результатам проверки подводятся итоги, и выявляется группа-победитель. Задания: Блок 1. 1. При каких значениях параметра а уравнение (а-2)х 2. При каких значениях а уравнение (а 3. При каком значении параметра а уравнение х2-2(а-1)х+а+5=0 имеет положительные корни? 4. При каком значении параметра а уравнение х2+(3а-5)х-2=0 имеет корни разных знаков? 5. При каком значении параметра а оба корня уравнения х2-(3а-2)х-6а=0 неотрицательны? 6. При каких значениях параметра k сумма корней уравнения х2-2 k (х-1)-1=0 равна сумме квадратов корней? 7. Пусть х1 и х2 – корни уравнения 2х2-7х-3=0. Составить квадратное уравнение, корнями которого являются числа 1/ x 1 и 1/ x 2 . 8. Не вычисляя корней уравнения 3х2+8х-1=0, найти х1/х2+х2/х1 . Блок 2. 1. При каком значении параметра а уравнения х2+(а 2. При каком значении параметра а корни трехчлена 3х2+(а 3. Найти все значения а, при которых имеет корни уравнение (2а+1)х 4. При каком значении а уравнения х2+ах+1=0 и х2+х+а=0 имеют общий корень? 5. При каких значениях параметра р сумма квадратов корней уравнения х2+(р-1)х+р 6. Найти наименьшее значение выражения х12 + х22, если х1 и х2 – корни уравнения х2 - 2ах + а + 6 = 0.
7. Корни х1 и х2 уравнения х2+рх+12=0 обладают свойством х2-х1=1. Найти р. 8. При каком значении а уравнение (а+4х-х 4. Подведение итогов занятия: - Подсчет количества верно решенных заданий у каждой команды, начисление командам баллов. - Определение уровня достижения целей урока и меру участия каждого учащегося в занятии, оценка работы школьников. В каждой группе заполняется таблица (Таблица 4), происходит распределение общего количества баллов между членами каждой команды. 5. Постановка домашнего задания: Каждый ученик должен выполнить любые пять заданий из блоков 1 и 2, которые не решал на занятии. Литература: [3], [4], [5], [8], [9], [12], [13], [16], [18], [25], [29], [32], [33].
|
|||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.120.100 (0.01 с.) |

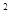 +(4-2а)х+3=0 имеет единственное решение?
+(4-2а)х+3=0 имеет единственное решение?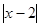 )=0 имеет 3 корня?
)=0 имеет 3 корня?


