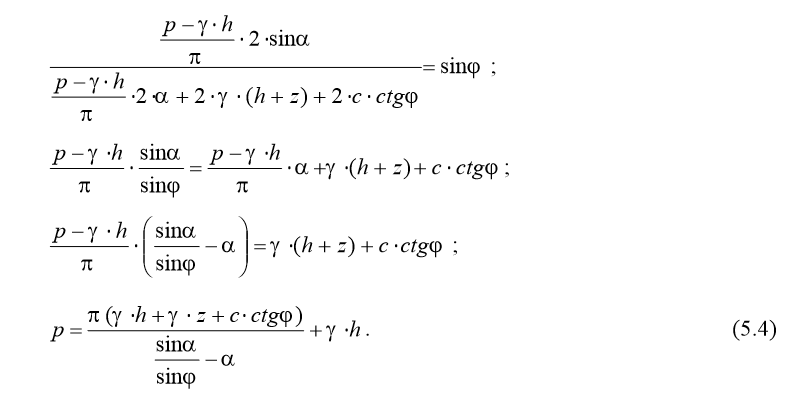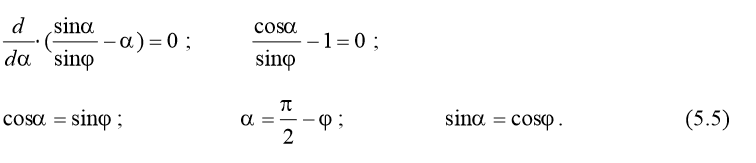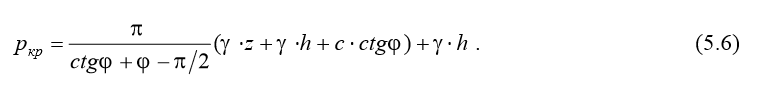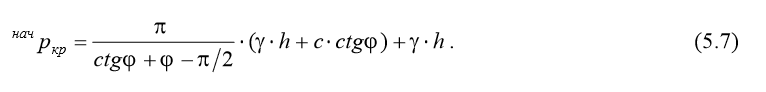Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 1. Введение в курс. Краткий исторический обзор. Строительные свойства грунтов. Основные закономерности механики грунтов. Закон уплотнения карла Терцаги.Стр 1 из 12Следующая ⇒
Лекция 1. Введение в курс. Краткий исторический обзор. Строительные свойства грунтов. Основные закономерности механики грунтов. Закон уплотнения Карла Терцаги. Содержание, цели и задачи курса Механика грунтов изучает проблемы прочности и устойчивости грунтовых массивов и определяет условия их использования в качестве оснований объектов строительства. Настоящий курс являются естественным продолжение курсов «Инженерная геология» и «Инженерные изыскания в строительстве». Основной целью курса является изложение основ инженерной теории расчета оснований по предельным состояниям I и II группы в интеграции с нормами строительного проектирования. Основными задачами, решаемыми в процессе изучения курса, являются: установление основных закономерностей механики грунтов и обобщение их в виде законов; изучение распределения напряжений в грунтовом массиве при действии различных нагружающих факторов; исследование прочности оснований и грунтовых массивов с использованием теории предельного равновесия; изучение методов расчета осадок оснований фундаментов, в том числе в условиях незавершенной консолидации грунтов, слагающих основание. Краткий исторический обзор Первой фундаментальной работой по механике грунтов принято считать исследование Кулона (Франция, 1773) по теории прочности сыпучих тел, известное в современной механике как закон Кулона-Мора. Академик Фусс (Россия, 1801) и инженер Винклер (Франция, 1867) предложили механические модели грунтового основания для расчета конструкций, взаимодействующих с грунтовой средой. Закономерности фильтрационных процессов в песчаных грунтах были впервые установлены Дарси (Франция, 1856) и обобщены в современной механике как закон ламинарной фильтрации Дарси. Труд профессора Буссинеска (Франция, 1885) “О распределении напряжений в упругой почве от сосредоточенной силы” до настоящего времени изучается в курсе механики грунтов и является основополагающим в теории распределения напряжений в грунтовой среде. Механика грунтов как самостоятельная дисциплина возникла с момента опубликования монографии профессора Терцаги (Германия, 1925) “Строительная механика грунтов”. Именно ему принадлежит установление основополагающей в теории расчета осадок зависимости, известной как закон уплотнения Терцаги. Существенное развитие
механика грунтов получила в работах ученых русской школы: Пузыревский (1923), Герсеванов (1931), Флорин (1936), Соколовский (1942), Егоров (1948), Березанцев (1948). Первый курс лекций по механике грунтов был подготовлен в СССР профессором Цытовичем (1934). Достижения украинских ученых в области механики грунтов отражены в работах Швеца В.Б., Гольдштейна М.Н., Клепикова С.Н. и др. Закон уплотнения Терцаги Закон уплотнения является одним из основных законов механики грунтов, основанным на допущении о том, что деформации грунта происходят, в основном, за счет изменения его пористости. В качестве предварительных замечаний отметим следующее. Грунт существенно отличается от таких строительных материалов как сталь, бетон и т.п. Крупнообломочные и песчаные грунты не обладают связностью. Связные пылевато-глинистые грунты имеют очень низкую прочность при одноосном сжатии. Все это создает большие проблемы при экспериментальном определении прочностных и деформационных характеристик грунтов. Поскольку не представляется возможным испытать грунт при одноосном напряженном состоянии (растяжение, сжатие), как это принято для большинства строительных материалов, для испытания грунтов используют схемы со сложным напряженным состоянием (см. курс "Инженерные изыскания в строительстве"). Одной из таких схем является схема осесимметричного компрессионного сжатия (рис. 1.3). Граничными условиями в такой схеме являются нулевые значения поперечных деформаций. Возникающие на боковых поверхностях цилиндрического образца давления не измеряются, а оцениваются теоретически. При этом касательные напряжения на этих поверхностях предполагаются равными нулю, в связи с чем вертикальное и боковое давления – суть главные напряжения. Ниже приводятся теоретические выкладки, связанные с приложениями закона уплотнения Терцаги, простейший вид которого уже рассматривался в курсе "Инженерные изыскания в строительстве".
Цилиндрический образец Грунта; 2 – жесткое кольцо с безфрикционной внутренней поверхностью; р – вертикальное давление; р W – давление в поровой воде; А g – площадь поперечного сечения грунта; h 0, hi – соответственно высота ненагруженного и нагруженного образца грунта; s x, s y, s z, t zx, t zy – Рис. 2.1. Фазы напряженно-деформированного состояния грунта: Рстр – структурная прочность; начРкр – начальное критическое давление; предРкр – предельное критическое давление; R – расчетное сопротивление грунта; 0 – фаза упругой работы; I – фаза уплотнения; II – фаза сдвигов; III – фаза выпоров; Зоны выпоров Фаза уплотнения соответствует уровням напряжений в грунте, в диапазоне которых процесс его деформирования удовлетворительно подчиняется закону уплотнения Терцаги. Линейная зависимость между деформациями и напряжениями в этой фазе не является обратимой. При разгрузке штампа из диапазона давлений, соответствующего фазе уплотнения, грунт деформируется по линейной зависимости, не совпадающей с ветвью нагрузки. При полной разгрузке штампа (рис. 1.5) имеет место необратимая (пластическая) осадка, соответствующая нулевым напряжениям по подошве. Повторное нагружение штампа до уровня напряжений, достигнутых перед разгрузкой, происходит по графику, совпадающему с графиком разгрузки. Нагружение выше этого уровня происходит по закону первичной нагрузки. Таким образом, закон уплотнения Терцаги устанавливает линейную зависимость между напряжением и суммой упругой и пластической деформации грунта. Указанная особенность закона уплотнения формулируется как принцип линейной деформируемости: при простом нагружении грунта в фазе его уплотнения сумма упругой и пластической деформации линейно зависит от действующего напряжения. Коэффициентом пропорциональности в этой линейной зависимости является модуль деформации грунта Е, названный так в отличие от модуля упругости, характеризующего деформацию упругого тела. Модуль упругости грунта Ее определяется по графику разгрузки и является коэффициентом пропорциональности между упругой деформацией грунта и действующим напряжением. Модуль деформации используется в статических расчетах, а модуль упругости – в динамических расчетах грунтовых оснований. Фаза сдвигов характеризует начало образования в грунте зон предельного равновесия. Зоной предельного равновесия в грунте называют геометрическое место точек, в которых не удовлетворяются условия прочности Кулона – Мора. Первоначально эти зоны образуются по краям штампа, где имеет место концентрация напряжений. Разрушение грунта сопровождается большими сдвиговыми деформациями, что нашло отражение в названии рассматриваемой фазы напряженно-деформированного состояния грунта. Уплотнение грунта в этой фазе практически не происходит. Грунт считается несжимаемым, а коэффициент Пуассона в этой фазе близок к 0,5. Давление на грунт, соответствующее началу фазы сдвигов, называют начальным критическим давлением – нач.ркр. Фаза выпора является следствием развития фазы сдвигов в области грунтового массива, являющегося основанием штампа, с образованием поверхностей скольжения, отделяющих основание штампа от нижележащего грунтового массива. В результате этого осадки штампа происходят без увеличения нагрузки за счет перемещения грунта основания из-под штампа по плоскостям скольжения с выходом на поверхность грунтового массива. При этом вокруг штампа происходит поднятие (выпор) грунта, что нашло отражение в названии этой фазы. Непосредственно под штампом в фазе выпора образуется коническая переуплотненная зона, называемая ядром жесткости. Прочность этой зоны обусловлена боковыми давлениями со стороны окружающего грунта, находящегося в состоянии пластического течения. Как известно, коэффициент бокового давления в грунте в состоянии пластического течения стремится к единице. Таким образом, жесткое ядро находится до исчерпания несущей способности основания в состоянии компрессионного сжатия, близкого к трехосному сжатию, что и определяет его высокую прочность. В зонах пластического течения недоуплотненные грунты получают дополнительное уплотнение, а переуплотненные – разуплотняются. Это явление называется дилатансией. Давление, при котором наступает фаза выпора, называется предельным критическим давлением – пред.ркр.
В соответствии с охарактеризованными выше фазами напряженнодеформированного состояния грунта применяются следующие его расчетные модели:
2. Закон прочности Кулона – Мора устанавливает условия, при которых грунт деформируется без увеличения напряжений за счет изменения формы. При этом его объемная деформация предполагается неизменной (принцип несжимаемости в стадии пластического течения). Из приведенного определения становится очевидным невозможность определения прочностных характеристик грунта в опыте на компрессионное сжатие. По этой причине используют схемы испытаний, в которых нагружение сопровождается развитием сдвиговых напряжений и деформаций. Нашли распространение следующие схемы испытаний: срез по фиксированной плоскости (испытание грунта в срезном приборе); плоский сдвиг объема грунта в состоянии компрессионного сжатия (скашивание образца грунта в срезном приборе); сжатие грунта в условиях переменного бокового давления (испытание в стабилометре). Наиболее надежные результаты дают испытания в стабилометре. Тем не менее, самым распространенным способом определения прочностных характеристик грунта является испытание его в срезном приборе.
Если понятие прочности связного грунта не выходит за рамки традиционных представлений о прочности строительных материалов, то понятие прочности несвязных (сыпучих) грунтов требует дополнительных пояснений. Например, литературная метафора «строить замки на песке» начисто отрицает наличие прочностных свойств у песчаных оснований. В то же самое время строительная практика утверждает, что основание из крупнозернистого песка являются одним из самых надежных видов оснований. Механизм прочности несвязных грунтов заключается в следующем. Под действием сжимающих напряжений в грунте, в том числе, вызванных его собственным весом, на контактных поверхностях минеральных частиц возникают силы трения, препятствующие взаимным перемещениям частиц. Кроме этого, между минеральными частицами, пересекающими условную плоскость, имеются зоны зацепления (взаимного проникновения), создающие нагельный эффект. Таким образом, при сдвиге грунта по фиксированной плоскости возникает реакция, равная сумме сил трения по контактным поверхностям минеральных частиц. После преодоления сил трения происходит сдвиг грунта по фиксированной плоскости. При наличии зацепления между частицами сдвиг сопровождается переупаковкой минеральных частиц скелета грунта (рис. 2.2). Переупаковка скелета вызывает вначале доуплотнение грунта (дилатация), а при дальнейшем сдвиге – разуплотнение грунта (контракция). В предельном состоянии сдвиг грунта по фиксированной плоскости происходит без увеличения сдвигающей нагрузки. Таким образом, прочность несвязного грунта определяется уровнем действующих в нем сжимающих напряжений. Совершенно очевидно, что такой грунт не имеет прочности при одноосном напряженном состоянии, однако может обладать достаточно высокой прочностью при других видах напряженного состояния, которые возникают в грунтовом массиве при передаче на него нагрузок от фундаментов.
Рис. 2.2. Схемы дилатансионных явлений в песчаных и крупнообломочных грунтах: а – исходное состояние; б – дилатация – доуплотнение от действия сдвиговых напряжений t; в – контракция – разуплотнение под действием сдвиговых напряжений t; h – исходная высота образца; D hd – уменьшение высоты образца за счет дилатации; D hk – увеличение высоты образца за счет контракции.
В первоначальном виде закон прочности сыпучей среды был сформулирован Кулоном в следующем виде: касательные напряжения на площадке сдвига в состоянии предельного равновесия грунта пропорциональны нормальным напряжениям, действующим на этой площадке. В последствии этот закон был распространен на связные грунты, обладающие отличной от нуля прочностью при нулевых значениях нормальных напряжений на площадке сдвига. На рис. 2.3 представлены графические построения, связанные с выводами различных форм представления закона прочности Кулона–Мора.
Для площадки сдвига закон прочности Кулона–Мора имеет математическое выражение, уже известное нам из курса "Инженерные изыскания в строительстве": τ = с + σ ⋅ tg ϕ, (2.1) где с – сцепление, параметр, соответствующий прочности грунта при нулевом значении нормального напряжения на площадке сдвига; tg ϕ – коэффициент пропорциональности, равный тангенсу угла внутреннего трения; ϕ– угол внутреннего трения; σ – эффективные нормальные напряжения на площадке среза. Примечание. Здесь под эффективными напряжениями следует понимать разницу между полными напряжениями и избыточным (по сравнению с атмосферным) давлением в поровой воде. Избыточное давление в поровой воде называют нейтральными напряжениями. Сумма эффективных и нейтральных напряжений всегда равна полному напряжению. Ниже (см. лекцию № 8) будет показано, что в условиях завершенной фильтрационной консолидации нейтральные напряжения равны нулю, а эффективные напряжения равны полным напряжениям. Таким образом, наличие порового давления снижает прочность грунта, а опыты по определению прочностных характеристик грунта должны проводиться по дренированно-консолидированной схеме. Формуле (2.1) на графике (рис. 2.3) соответствует прямая, наклоненная к оси нормальных напряжений σ под углом внутреннего трения грунта ϕ и отсекающая на оси касательных напряжений τ отрезок, численно равный сцеплению грунта с. Указанная прямая является огибающей предельных кругов Мора, соответствующих прочности грунта при различных уровнях нормальных напряжений на площадке сдвига. График по формуле (2.1) называют также графиком прочности грунта, диаграммой прочности грунта или паспортом прочности грунта. В соответствии с формулой (2.1) прочность грунта неограниченно возрастает при неограниченном увеличении нормальных напряжений на площадке сдвига. Последнее не согласуется с экспериментальными данными. Это объясняется тем, что при определенном уровне сжимающих напряжений в грунте происходят микроразрушения на контактах минеральных частиц, сдерживающие рост сил внутреннего трения. При очень высоком уровне сжимающих напряжений происходит разрушение материала минеральных частиц, и график прочности ниспадает до пересечения с осью нормальных напряжений. Однако уровень таких напряжений значительно превосходит уровень напряжений, действующих в основании фундаментов вплоть до исчерпания несущей способности основания. В связи с этим в практических расчетах оснований используют линейное уравнение прочности (2.1). Уравнение (2.1) может быть использовано только в том случае, если заранее известна площадка сдвига, например, при плоском сдвиге фундамента относительно основания. В большинстве же случаев площадка сдвига заранее неизвестна. Поэтому представляют практический интерес другие формы записи уравнения прочности (2.1). Уравнения прочности в главных напряжениях. Предельному состоянию грунта в точке А на графике прочности соответствует круг Мора, касающийся графика прочности в точке А, с главными напряжениями σ 1 и σ 2 (σ 1 >σ 2). Как известно, центр круга Мора отстоит от начала осей координат на расстоянии (σ 1 + σ 2) / 2, а его радиус равен (σ 1 -σ 2) / 2. Уравнение прочности в главных напряжениях вытекает из следующих преобразований:
Уравнение (2.2) можно преобразовать к виду, содержащему отношение главных напряжений:
Если в уравнениях (2.3) положить сцепление с равным нулю, то величина tg 2 (45° - ϕ / 2) будет представлять собой коэффициент бокового давления сыпучей среды в предельном состоянии. Этот коэффициент называют также коэффициентом активного давления. В отличие от этого коэффициент tg 2 (45° + ϕ / 2) называют коэффициентом пассивного давления. Он позволяет вычислить действующее напряжение при известном боковом давлении в сыпучей среде. При ϕ = 0 говорят, что среда является идеально связной. Полученное в лекции № 1 выражение для коэффициента бокового давления через коэффициент Пуассона справедливо в предельном состоянии только для идеально связной среды, например, для пластичной глины. Для сыпучей среды коэффициент бокового давления в предельном состоянии остается меньшим единицы. Уравнение прочности в компонентах тензора напряжений. Основным неудобством в применении уравнений (2.3) является необходимость вычисления в грунтовом массиве главных напряжений. Этого можно избежать подстановкой в уравнение (2.2) значений главных напряжений, выраженных через компоненты тензора напряжений:
3. Закон ламинарной фильтрации Дарси устанавливает зависимость скорости фильтрации поровой воды от градиента гидравлического напора. Как уже отмечалось, грунт является открытой термодинамической системой в отношении массопереноса в форме движения поровой воды. Движение поровой воды называют фильтрацией, а связанные с этим процессы – фильтрационными. Рассматриваются такие скорости, при которых не наблюдаются завихрения гидравлического потока. Такое движение характеризуется как спокойное или ламинарное. Гидравлическим напором называют давление в поровой воде, выраженное в единицах высоты эквивалентного водяного столба: H = p / γ w, где γ w – удельный вес воды. Градиентом гидравлического напора называют безразмерную величину, равную отношению разности гидравлических напоров на входе и выходе фильтрационного потока к длине пути фильтрации поровой воды: i = (Нвх . – Нвых .) / L = tg j (рис. 2.4 б). В опытах (рис. 2.4 а) Дарси измерял расход воды (м3) при фильтрации ее через цилиндр с песком площадью поперечного сечения А. Им получена следующая экспериментальная зависимость: Q = kf ⋅ i ⋅ A ⋅ t, где kf – коэффициент пропорциональности, названный коэффициентом фильтрации; t – время фильтрации.
Определим понятие скорости фильтрации q (м/с) как расход поровой воды через единицу поперечного сечения в единицу времени. Тогда из экспериментальной зависимости Дарси будем иметь: q = kf ⋅ i. (2.5) Формула (2.5) уже рассматривалась в курсе "Инженерные изыскания в строительстве" и известна как закон ламинарной фильтрации Дарси, который можно сформулировать следующим образом: скорость фильтрации поровой воды прямо пропорциональна градиенту гидравлического напора. Коэффициент фильтрации kf, входящий в формулу (2.5), можно трактовать как скорость фильтрации поровой воды при градиенте гидравлического напора (говорят также, гидравлическом градиенте), равном единице. В соответствии с рисунком (2.4 б) единичному значению градиента гидравлического напора соответствует угол наклона поверхности грунтового потока к горизонтальной плоскости j = 45°. Из приведенного выше определения следует, что коэффициент фильтрации имеет размерность скорости (м/с). В справочных материалах коэффициент фильтрации чаще всего приводится в м/сутки. Значения коэффициента фильтрации зависят от вида грунта и изменяются в широких пределах от 0,001 м/сутки для глин до 100 м/сутки для песков. В формуле (2.5) фигурирует фиктивная скорость фильтрации, отнесенная к полному сечению грунта, включающему как сечения пор, так и сечения минеральных частиц. Так как фильтрация происходит только по сечениям пор, действительная скорость фильтрации выше фиктивной. Она может быть вычислена через пористость грунта: v = q / n. Действительная скорость учитывается при анализе суффозионных процессов в грунтах. Реальные грунты обладают начальным гидравлическим сопротивлением. Это означает, что фильтрационные процессы протекают лишь при гидравлических градиентах, больших определенной величины. Эту величину называют начальным гидравлическим градиентом i 0. Величина начального гидравлического градиента, как и коэффициент фильтрации, зависит от вида грунта. С учетом сделанного замечания, запишем окончательное выражение для закона ламинарной фильтрации Дарси: q = kf ⋅ (i – i 0). (2.6) Рис. 3.2. Напряжение в грунтовом массиве от действия группы сил.
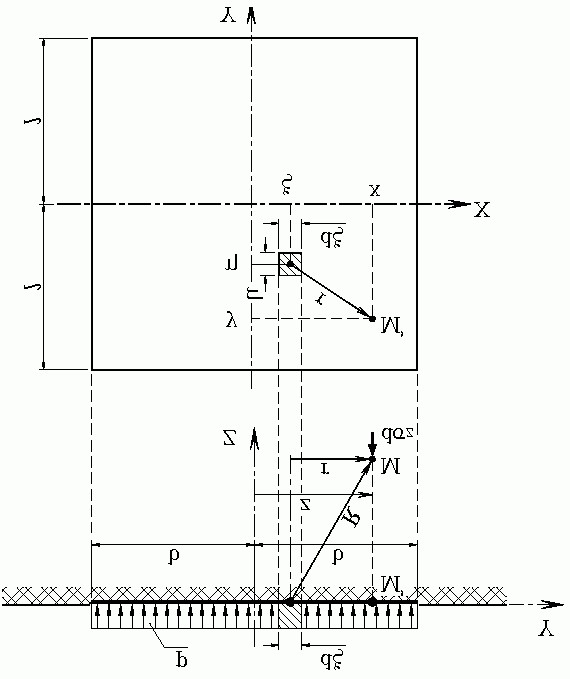
Анализ формулы (3.7) позволяет сделать следующий практически важный вывод: при неизменных давлениях на основание увеличение площади его нагружения приводит к увеличению напряжений в грунтовом массиве. 3. Напряжения от нагрузки, распределенной по прямоугольнику. Эта задача имеет большое прикладное значение, т.к. большинство фундаментов имеют прямоугольную форму подошвы в плане. Кроме этого, при определении напряжений от распределенной нагрузки разрешается некорректность формул (3.5) и (3.6) при z = 0. Изобразим загруженную поверхность в плане (рис. 3.3). Совместим оси координат с центральными осями прямоугольника, ограничивающего загруженную давлением р (кПа) поверхность. Обозначим размеры прямоугольника: L, B – длина и ширина; l, b – полудлина и полуширина. Выделим на загруженной поверхности бесконечно малую площадку с координатами в центре площадки ξ и η и площадью d ξ⋅ d η. Элементарная сила, действующая на площадку, будет равна: dP = p ⋅ d ξ⋅ d η. Определим напряжение d σ z в грунтовом массиве в точке с координатами x, y, z от элементарной силы dP, воспользовавшись формулой Буссинеска (3.5):
Рис. 3.3. Напряжение от нагрузки, распределенной по прямоугольнику: Р – интенсивность нагрузки; l, b – полудлина и полуширина площади нагрузки.
В формуле (3.8) учтено, что радиус-вектор R соединяет точку с координатами x, y, z, в которой определяется напряжение, и точку с координатами ξ, η, 0, в которой действует элементарная сила. Для определения напряжения σ z в точке с координатами x, y, z от всей загруженной площади проинтегрируем выражение (3.8) по загруженной площади:
Интеграл по формуле (3.9) имеет замкнутое аналитическое решение в тригонометрических функциях, впервые полученное в 1935 г. А. Лявом. Наиболее простые выражения для напряжений получаются по вертикалям в центральном сечении загруженной площади и по угловым точкам: σ z = α⋅ p; σ zc = α c ⋅ p, где
Формулы (3.10) использованы в СНиП на проектирование оснований для вычисления напряжений под подошвой фундамента в центральном сечении и в угловой точке. Анализ выражений (3.10) позволяет сформулировать следующее определение: напряжения в угловой точке на глубине z равны ¼ напряжений в центральной точке на глубине z / 2. Это определение использовано в СНиП на проектирование оснований для вычисления коэффициента α с по табулированному значению коэффициента α. 4. Метод угловых точек. Основывается по аналогии с формулой (3.7) на принципе суперпозиции. При этом для вычисления напряжений в любой точке грунтового массива используются формулы (3.10). Графические построения, связанные с техникой применения метода угловых точек для определения напряжений в грунтовом массиве, представлены на рис. 3.4. Различают два принципиально отличных случая применения метода угловых точек: вертикаль, по которой определяются напряжения, находится в пределах загруженной площади; вертикаль, по которой определяются напряжения, находится за пределами загруженной площади.
Рис. 3.4. Метод угловых точек: а – точка М расположена в пределах загруженной площади; б – точка расположена за пределами загруженной площади; в – точка М расположена за пределами загруженной площади в створе загруженной площади. В первом случае (рис. 3.4 а) загруженная площадь разбивается на четыре прямоугольника, для которых точка, в которой определяется напряжение, является угловой. Напряжения определяются по формуле:
где αc,i – коэффициенты по формуле (3.10) для прямоугольников 1 – 4. Во втором случае (рис. 3.4 б) строится фиктивная площадь нагружения, границами которой являются две стороны прямоугольника с действительной нагрузкой, и точка, в которой определяется напряжение. Незагруженная площадь в фиктивном прямоугольнике разделяется на два пересекающихся прямоугольника, для которых, как и в первом случае, точка, в которой определяется напряжение, является угловой. Рассматриваются: прямоугольник, образующий фиктивную площадь нагружения (α с,f); два пересекающихся прямоугольника (α с,1 и α с,2); прямоугольник области пересечения (α с,cr). Напряжение вычисляется по формуле: σ z = p (α c, f −α c,1 −α c,2 +α c, cr). (3.12) Здесь слагаемое, учитывающее влияние области пересечения, несмотря на отсутствие на ней нагрузки, входит в формулу со знаком «+», компенсируя тем самым двойное вычитание по этой области предыдущими членами формулы. Обобщая формулы (3.11) и (3.12), можно дать следующее определение методу угловых точек: напряжение в произвольной точке от нагрузки, распределенной по прямоугольной площади, равно алгебраической сумме напряжений в угловых точках прямоугольников, для которых рассматриваемая точка является угловой, при этом алгебраическая сумма площадей этих прямоугольников с учетом знаков в формуле суммирования напряжений должна совпадать с фактической площадью нагрузки. Используя это определение, непосредственно вытекающее из принципа суперпозиции, можно предложить самые различные схемы реализации метода угловых точек, например, для случая, представленного на рис. 3.4 в: σ z = p (α c, f 1 +α c f 2 −α c,1 −α c,2). (3.13)
Лекция 5. Теория предельного напряженного состояния грунта. Задача Пузыревского. Начальные и предельные критические давления. Огибающие зон предельного равновесия. Давление грунта на подпорные стены. Устойчивость подпорных стен. Предельное напряженное состояние грунта принято анализировать методами предельного равновесия. В современной механике грунтов применяются также методы, основанные на решении смешанной задачи теории упругости и теории пластичности, а также методы теории пластического течения. Уравнения метода предельного равновесия для условий плоской задачи имеют вид:
где σ y, σ z, τ yz – компоненты тензора напряжений; γ – удельный вес грунта; c, ϕ – параметры прочности грунта. Решение системы уравнений (5.1) совместно с краевыми условиями позволяет установить зоны, в которых грунт находится в состоянии предельного равновесия. 1. Предельное напряженное состояние грунта под полосовой нагрузкой. Задача Пузыревского. Основными гипотезами, при которых решена задача Пузыревского, являются следующие: 1) компоненты напряжений распределяются в грунтовом массиве в соответствии с решением Фламана для плоской деформации; 2) коэффициент бокового давления грунта в предельном состоянии равен единице. Экспериментальными исследованиями установлено, что введенные гипотезы позволяют получать решения с точностью, достаточной для практики. Пусть на поверхности грунтового массива (рис. 5.1) задана полосовая нагрузка интенсивностью p - γ⋅ h и бесконечно протяженная распределенная нагрузка интенсивностью γ⋅ h, так что в пределах полосы суммарная интенсивность нагрузки составляет р (кН/м2). Нагрузку γ⋅ h можно рассматривать как пригруз поверхности грунтового массива насыпью высотой h. Напряжения в грунтовом массиве будут складываться из напряжений от полосовой нагрузки интенсивностью p - γ⋅ h и напряжений от собственного веса грунта с учетом насыпи на его поверхности высотой h. Используя формулы для определения указанных напряжений, полученные ранее, будем иметь:
Полученные формулы являются решением системы дифференциальных уравнений равновесия (5.1) применительно к рассматриваемой задаче. Условие предельного равновесия примем в форме закона Кулона–Мора для главных напряжений: Подставляя напряжения (5.2) в формулу (5.3), получим уравнение предельного равновесия весомого грунта под полосовой нагрузкой с учетом пригруза на поверхности:
Полученное уравнение предельного равновесия устанавливает зависимость между интенсивностью полосовой нагрузки р и координатами точки предельного равновесия z и α. Варьируя значениями координат z и α, можно установить области пластического деформирования грунта при р = const. Такие решения справедливы для малых областей пластического деформирования и весьма приближенны для развитых пластических зон. Объясняется это тем, что в основе формулы (5.4) лежит решение о распределении напряжений в грунтовом массиве в упругой постановке. В действительности напряжения в пластических зонах не подчиняются законам упругости. Поэтому с развитием пластических зон уменьшается достоверность результатов решения задачи по формуле (5.4). Практический интерес представляет минимальное значение полосовой нагрузки при развитии зон пластического деформирования на глубину z. Этому значению нагрузки соответствует максимальное значение знаменателя в формуле (5.4). Значение координаты α, соответствующее максимальному значению знаменателя, определяется из уравнения:
Подстановкой выражений (5.5) в формулу (5.4) получаем критическое значение полосовой нагрузки, соответствующее развитию зон пластического деформирования на глубину z:
Начальным критическим давлением называют интенсивность нагрузки, которая соответствует началу образования зон пластического деформирования. Таким образом, начальное критическое давление при полосовой нагрузке может быть определено по формуле (5.6) при подстановке в нее нулевого значения координаты z:
Выражение (5.7) является формулой Пузыревского, полученной им для равномерно распределенной нагрузки по полосе в условиях плоской деформации. Имеются аналогичные решения для других видов напряженного состояния и нагрузок, например, решение Прандтля для осесимметричной пространств
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 567; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.54.63 (0.083 с.) |
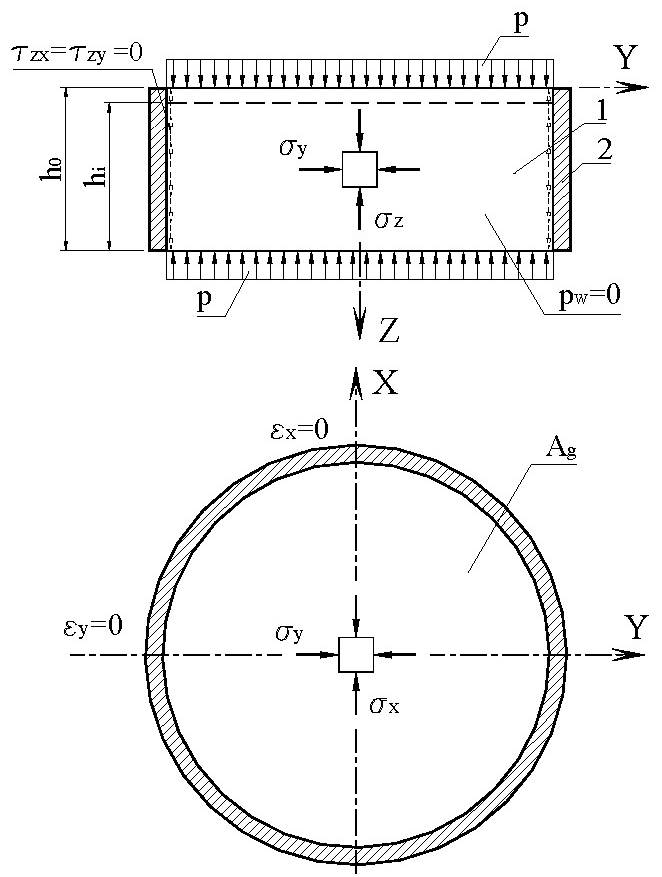 Рис. 1.3. Напряженное состояние грунта в виде осесимметричного компрессионного сжатия:
Рис. 1.3. Напряженное состояние грунта в виде осесимметричного компрессионного сжатия: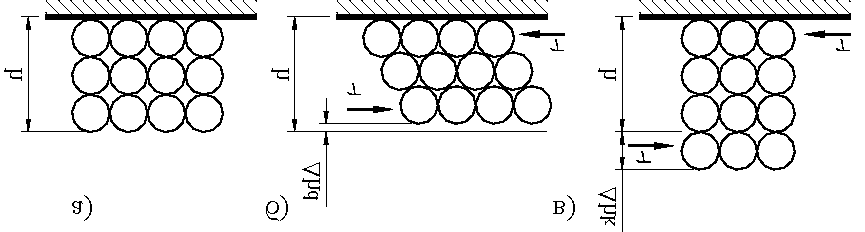
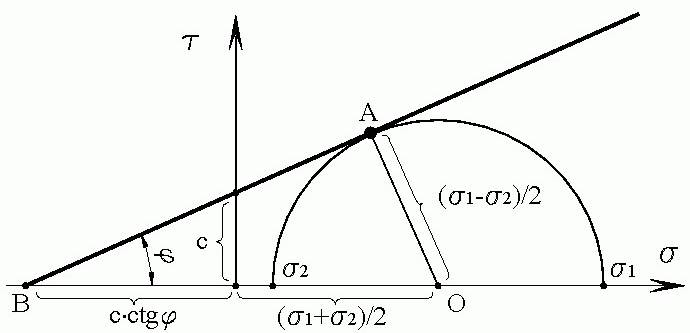 Рис. 2.3. Графическое построение для вывода уравнения закона прочности Кулона-Мора
Рис. 2.3. Графическое построение для вывода уравнения закона прочности Кулона-Мора
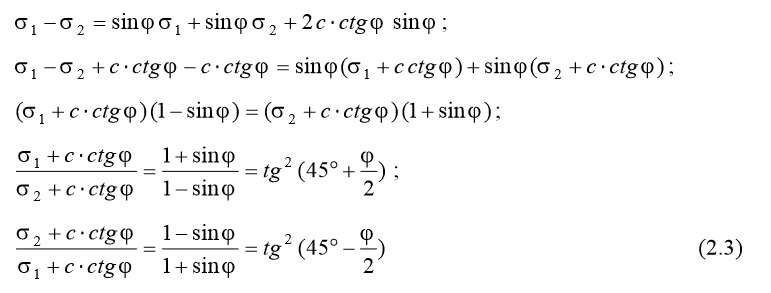
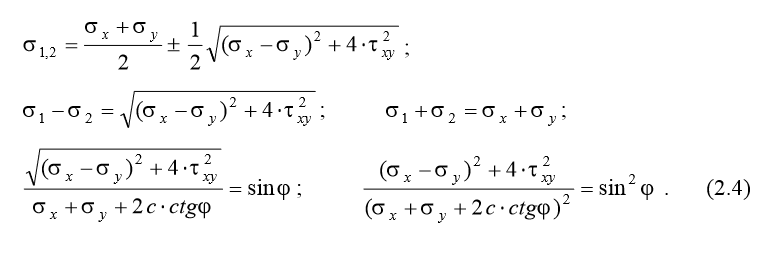

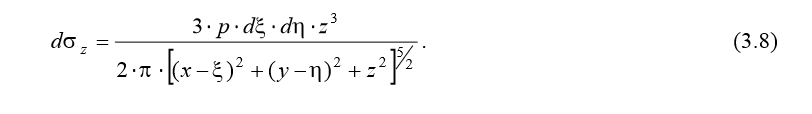
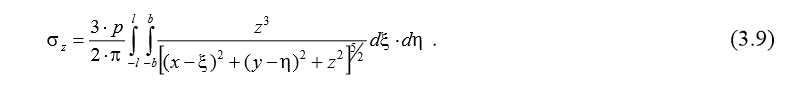
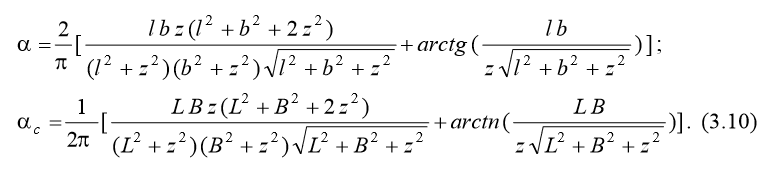


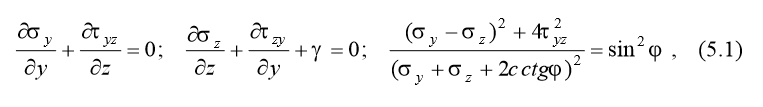
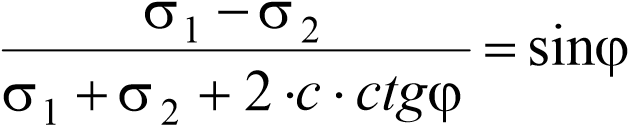 ; (5.3)
; (5.3)