Краткие теоретические и учебно-методические материалы по теме практической работы

При работе бруса на растяжение (сжатие) в его поперечных сечениях возникает продольная сила N. Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на его продольную ось всех внешних сил, приложенных по одну сторону от проведенного сечения.

  Для расчета на прочность и определение перемещений поперечных сечений бруса надо знать закон изменения продольных сил по его длине.

  При растяжении продольную силу будем считать положительной,при сжатии – отрицательной.

  Условие прочности при растяжении и сжатии имеет вид:

σ = N / F ≤ [ σ ],

где σ, N – соответственно нормальное напряжение и продольная сила в опасном сечении (т.е. сечении, в котором возникают наибольшие напряжения);

 F – площадь поперечного сечения бруса; [σ] – допускаемое напряжение.

 

  Исходя из условия прочности, можно решать три вида задач: 1. Проверка прочности. 2. Подбор сечения F ≥ N / [σ]. 3. Определение допускаемой нагрузки [N] ≤ [σ] F.

  Продольные деформации при осевом растяжении и сжатии определяются по закону Гука:

ε = σ / E,

где σ – напряжение в поперечном сечении;

E – модуль продольной упругости.

  Абсолютные удлинения (укорочения) стержней при осевом растяжении (сжатии) определяются по формуле:

∆ℓ = Nℓ / (EF)

  Учитывая, что N / F = σ, формулу для абсолютного удлинения ∆ℓ можно представить в виде                                                    

∆ℓ = σℓ / E.

В таком виде формула удобна в тех случаях, когда предварительно определены напряжения.

Для ступенчатого бруса удлинение (укорочение) определяются по формуле

∆ℓ = ∑∆ℓ_i = ∑ N_iℓ_i / E

F_i = ∑ σ_iℓ_i / E,

где N_i, ℓ_i, F_i –соответственно продольная сила, длина и площадь сечения в пределах каждого участка стержня.

 

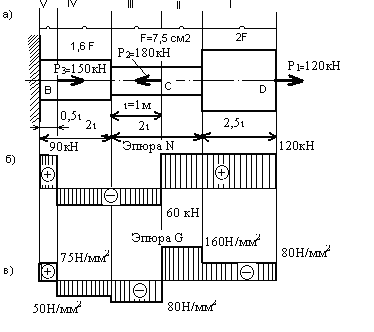
Пример по выполнению практической работы

Для заданного ступенчатого бруса (рис.1,а) построить эпюры продольных сил и нормальных напряжений по его длине, а также определить перемещения свободного конца и сечения С, где приложена сила P_2. Модуль продольной упругости материала Е = 2,1 ∙ 10⁵ Н/мм².

Решение. Заданный брус имеет пять участков I, II, III, IV, V (рис.1,а). Эпюра продольных сил показана на рис.1.б.

Вычислим напряжения в поперечных сечениях каждого участка:

для первого

σ₁= N₁/F₁= 120 ∙ 10³/1500 = 80 H/мм²;

для второго

σ₂= N₂/F₂ = 120 ∙ 10³/ 750 = 160 Н/мм²;

для третьего

σ₃ = N₃/F₃ = − 60 ∙ 10³/ 750 = − 80 H/мм²;

для четвертого

σ₄ = N₄/F₄ = − 60 ∙ 10³/ 1200 = − 50 Н/мм²;

для пятого

σ₅ = N₅/F₅ = 90 ∙ 10³/ 1200 = 75 H/мм²;

 

Эпюра нормальных напряжений построена на рис.1,в

 

Рисунок 1

 

  Перейдем к определению перемещений поперечных сечений. Перемещение свободного конца бруса определяется как алгебраическая сумма удлинений (укорочений) всех его участков:

∆ℓ = ∆ℓ₁ + ∆ℓ₂ + ∆ℓ₃ + ∆ℓ₄ + ∆ℓ₅ = σ₁ℓ₁/E + σ₂ℓ₂/E + σ₃ℓ₃/E + σ₄ℓ₄/E + σ₅ℓ₅/E.

  Подставляя числовые значения, получаем

                           1

∆ℓ= ———— (80 ∙ 2500 + 160 ∙ 1000 − 80 ∙ 1000 − 50 ∙1500 + 75 ∙ 500)= 1,15 мм.

                        2,1 ∙ 10⁵

     Перемещение сечения С, в котором приложена сила Р₂, определяется как алгебраическая сумма удлинений (укорочений) участков III, IV,V:

∆ℓ_c=∆ℓ₃ + ∆ℓ₄ + ∆ℓ₅ = σ₃ℓ₃/E + σ₄ℓ₄/E + σ₅ℓ₅/E.

  Подставляя значения из предыдущего расчета, получаем

                                                         1000

∆ℓ_c = ———— (− 80 − 75 + 37,5) = −0,56 мм.

                                                        2,1 ∙ 10⁵

  Таким образом, свободный правый конец бруса перемещается вправо, а сечение, где приложена сила Р₂, - влево.

   Вычисленные выше значения перемещений можно получить и другим путем, пользуясь принципом независимости действия сил Р₁, Р₂, Р₃ в отдельности и суммируя результаты.

    Определить какое напряжение возникает в стальном стержне длиной ℓ=200 мм, если после приложения к нему растягивающих сил его длина стала ℓ₁=200,2 мм.

Е = 2,1 ∙ 10⁵ Н/мм².

    Решение. Абсолютное удлинение стержня ∆ℓ = ℓ₁− ℓ = 200,2 − 200 = 0,2 мм.

     Продольная деформация стержня  ε = ∆ℓ/ℓ = 0,2/200 = 0,001.

     Согласно закону Гука σ = Еε = 2,1 ∙10⁵ ∙ 0,001 = 210 Н/мм².

 

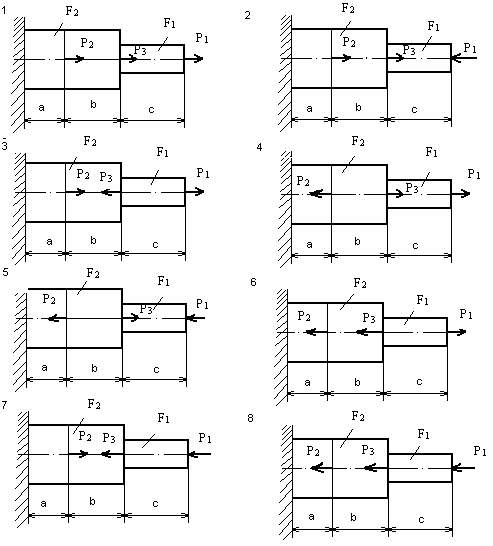
Задания для практического занятия:

Построить эпюры продольных сил и нормальных напряжений, а так же определить перемещение.

1.Изобразить расчетную схему бруса и приложить заданные силы. При необходимости определить опорную реакцию из уравнения равновесия.

2.Брус разбить на участки соответственно точками приложения сил.

3. Определить по методу сечений продольную силу для каждого участка.

4. Брус разбить на участки по точкам приложения сил и в местах, где изменяется площадь поперечного сечения построить эпюры напряжений.

5. Определить перемещение свободного конца бруса Е = 2,1 ∙ 10⁵ Н/мм²

6. Проверить прочность бруса.

 

Вари- ант	Схема	Р1	Р2	Р3	F1	F2	a	b	c
		кН			мм^2		м
1 2 3 4 5 6 7 8 9 10	1 2 3 4 5 6 7 8 1 2	12 13 11 10 15 14,5 16 15,5 18 17,5	6 5 8 9 7 8,5 9 7,5 22 23	12 12 13 14 30 27 27,5 28,5 9 8	120 110 130 125 100 125 130 140 160 150	260 270 280 250 320 310 300 350 360 350	0,2 0,25 0,35 0,4 0,15 0,18 0,22 0,25 0,20 0,22	0,4 0,45 0,35 0,25 0,4 0,25 0,35 0,45 0,50 0,48	0.6 0,5 0,4 0,5 0,55 0,65 0,70 0,75 0,65 0,70

 

 

Контрольные вопросы

1. Как нужно нагрузить прямой брус, чтобы он испытывал только растяжение (сжатие)?

2. Как распределяются напряжения по поперечному сечению бруса при растяжении (сжатии).

3. Зависит ли возникающее при растяжении (сжатии) напряжение: а) от материала бруса; б) от формы поперечного сечения? Зависит ли удлинение бруса от его материала?

 

 

 

Практическая работа № 5

 «Расчет соединения, работающего на срез и смятие»

Учебная цель: Рассчитатьзаклепочное соединение в стык и проверить прочность заклепочного соединения.

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

- определять площади среза и смятия;

знать:

- внутренние силовые факторы, напряжения и деформации при сдвиге и смятии;

- условия прочности.