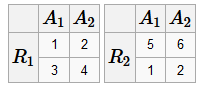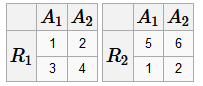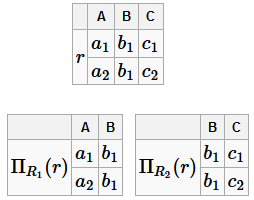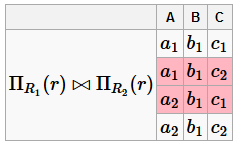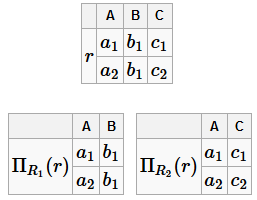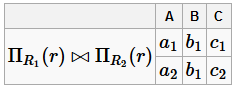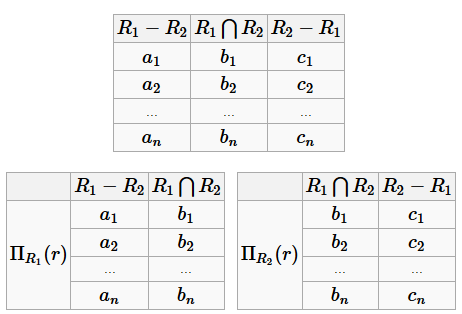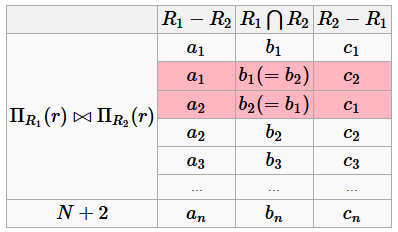Лекция №1 - Операции реляционной алгебры

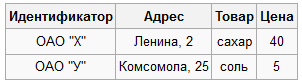
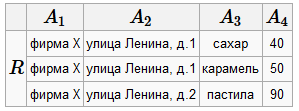
Лекция №1 - Операции реляционной алгебры

Определения

Схема отношения

Это поименованная совокупность атрибутов.

R =(A 1,..., A n), где A i - некоторый атрибут из домена отношения.

R =(идентификатор поставщика, адрес, товар, цена)=(A 1, A 2, A 3, A 4).

Здесь (A 1, A 3) - ключ, определяющий запись.

Степень схемы отношения

Это количество атрибутов в схеме.

Для R =(A 1, A 2, A 3, A 4) степень равна 4.

Экземпляр отношения

Это конкретная таблица с данной схемой отношения.

R =(идентификатор поставщика, адрес, товар, цена).

Кортеж

Любая одна строка в таблице экземпляра отношения.

Схема БД

A - множество всех атрибутов некоторой предметной области (универсальная схема отношения).

R 1,..., R n - совокупность атрибутов.

Тогда ρ =(R 1,..., R n) называется схемой БД.

Пример:

A =(A 1, A 2, A 3, A 4)

и две схемы: R 1=(A 1, A 2) и R 2=(A 1, A 3, A 4)

Так как R 1⋃ R 2= A, то ρ =(R 1, R 2).

Примеры схем БД

Пример "плохой" схемы БД

Пусть A =(идентификатор поставщика, адрес, товар, цена)

и есть одна схема ρ = R 1= A

Данная схема БД обладает следующими недостатками (аномалиями):

• избыточность. Адрес поставщика повторяется для каждого поставляемого им товара;
• потенциальная противоречивость. Если у поставщика меняется адрес, то его необходимо изменить во всех кортежах, в которые он входит;
• аномалия включения кортежа. В выбранном отношении R 1 пара атрибутов идентификатор-товар является ключом. При включении новой записи, атрибуты ключа не должны быть пустыми, поэтому в БД нельзя включить поставщика, если он в данный момент не поставляет товар;
• аномалия удаления. При удалении всех товаров, поставляемых поставщиком, теряется информация о самом поставщике.

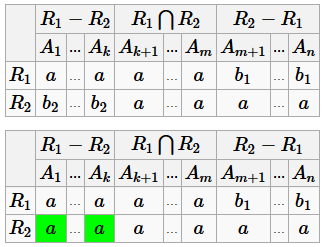
Первопричиной этих недостатков является то, что R 1 не находится в 3НФ

Пример "хорошей" схемы БД

Пусть A =(идентификатор поставщика, адрес, товар, цена)

R 1=(идентификатор, адрес)

R 2=(товар, цена)

Схема ρ =(R 1, R 2) находится в 3НФ и не обладает перечисленными выше недостатками.

Основные операции реляционной алгебры

Объединение отношений

R = R 1⋃ R 2

Объединение отношений - это отношение, каждый кортеж которого принадлежит либо R 1, либо R 2.

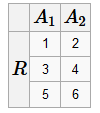
Дублирование кортежей не допускается.

Пересечение отношений

R = R 1⋂ R 2

Пересечение отношений - это отношение, каждый кортеж которого принадлежит и R 1, и R 2

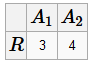
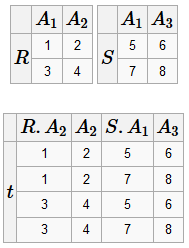
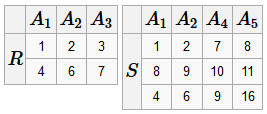
Декартово произведение

R, S - две схемы отношения со степенями k 1 и k 2

t = R × S

Декартово произведение - это отношение t со степенью k 1+ k 2, кортежи которого получаются конкатенацией кортежей из отношений R и S.

Проекция

t =Π A i 1... A ik (R)

Проекция - это отношение, каждый кортеж которого состоит из значений атрибутов A i 1... A ik исходного отношения R.

Селекция

t = σ F (R)

Селекция - это отношение, каждый кортеж которого принадлежит исходному отношению R и удовлетворяет логическому условию F.

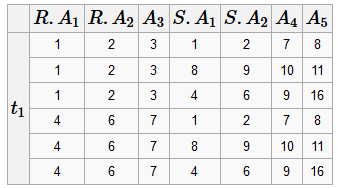
Естественное соединение

t = R ⋈ S

Определение этой операции следует из способа построения естественного соединения.

Построение естественного соединения:

1) построить декартово произведение R × S

2) выбрать из этого произведения кортежи по условию R. A i 1= S. A i 1... R. A ik = S. A ik, где A i... A k - общие атрибуты в схемах отношений R и S (предполагается, что эти атрибуты занимают одинаковое положение в отношениях. Хотя не обязательно)

3) удалить из полученного отношения S. A i 1... S. A ik, потому что они будут дублирующими.

 

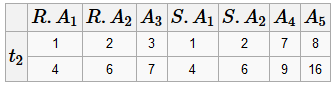
Функциональные зависимости

Пусть R =(A 1... A n) является функциональной схемой отношения и X, Y - некоторые подмножества атрибутов этой схемы. Говорят, что X функционально определяет Y (X → Y), если в любом экземпляре отношения со схемой R не существует двух кортежей, совпадающих по подмножеству X и не совпадающих по подмножеству Y

Иначе говоря, если два кортежа совпадают по X, то они должны совпадать и по Y

Например, R =(A 1, A 2, A 3, A 4), есть зависимости:

• A 1→ A 2 (1)
• A 1 A 3→ A 4 (2)

Предположим, что имеет место один экземпляр отношения со схемой R

Вторая ФЗ (2) имеет место быть, так как нет двух кортежей, совпадающих по этой паре (по крайней мере, в приведённом экземпляре схемы отношения, а других мы не знаем).

А первая ФЗ (1) не имеет место быть (в третьей строке другой номер дома портит всю картину).

Аксиомы Армстронга

Или правила вывода функциональной зависимости. Существуют различные интерпретации аксиом, но все эквивалентны. Потому приведём только один вариант.

Аксиомы Армстронга являются надёжными и полными.

Надёжность - если ФЗ выводится с помощью аксиом Армстронга, то она справедлива во всех экземплярах отношения, где справедливы исходные ФЗ F

Полнота - если имеет место какая-либо ФЗ, то она обязательно может быть выведена с помощью аксиом Армстронга.

Рефлексивность

Если Y ⊆ X ⊆ R

то X → Y. Тривиальная аксиома.

Дополнение

Если X → Y и Z ⊆ R (Z может быть пустым),

тогда X ⋃ Z → Y ⋃ Z или XZ → YZ

Транзитивность

Если X → Y, а Y → Z,

то X → Z

Пример построения множества ФЗ

Пусть задана УСО (универсальная схема отношения) R =(A, B, C) и зависимости F =(A → B, B → C)

1. A → A, B → B, C → C, AB → A, AB → B, AC → A, AC → C, BC → B, BC → C, ABC → A, ABC → C, AB → AB, AC → AC, BC → BC, ABC → AB, ABC → AC, ABC → BC, ABC → ABC
2. A → AB (1ФЗ и пополняем A), AC → BC, B → BC (2 ФЗ и пополняем B), AB → AC, AC → ABC, AB → ABC, AB → BC, A → AC
3. A → C (1 и 2 ФЗ), A → ABC

Всё, замыкание (F +) построено. Все перечисленные зависимости образуют замыкание.

Лемма

Справедливы следующие правила. Для их доказательства необходимо пополнить ФЗ так, чтобы можно было использовать аксиомы.

Правило объединения

Если X → Y и X → Z, то X → YZ

Доказательство:

1. X → XY (1 ФЗ и пополняем X);
2. XY → YZ (2 ФЗ и пополняем Y);
3. X → YZ (по аксиоме транзитивности).

Правило декомпозиции

Если X → Y, а Z ⊆ Y, то X → Z

Доказательство:

1. X → Y (по условию);
2. Y → Z (по аксиоме рефлексивности);
3. X → Z (по аксиоме транзитивности).

Алгоритм построения

Алгоритм является итерационной процедурой.

1. полагаем i =0 и X +0= X, а X + i - замыкание множества атрибутов на i-том шаге;
2. X + i +1= X + i ⋃ V, где V - такое множество атрибутов в F, что существует ФЗ Y → Z, где Y ⊆ X + i, V ⊆ Z;
3. если X + i +1= X + i, то X += X + i, иначе i = i +1 и возвращаемся в пункт 2.

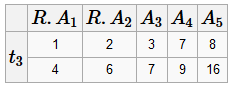
Пример построения

Пусть R =(A, B, C, D, E, G)

F =(AB → C, C → A, BC → D, ACD → B, D → EG, BE → C, CG → BD, CE → AG)

X = BD

Надо построить X +:

1) i =0, X +0= BD

2)

Получили, что X +4= X +3, а значит X += X +3= BDEGCA

Это означает, что имеют место следующие ФЗ: BD → B, BD → D, BD → E, BD → G, BD → C, BD → A, и все они ⊆ F +

Короче, чтобы проверить X → Y ⊆ F +, необходимо построить X +

 

Доказательство

1)

Докажем, что если ФЗ X → Y ∈ F (из этого следует, что Y ⊆ X + (1) по определению замыкания множества аттрибутов), то эта ФЗ принадежит G +

По построению G имеет место ФЗ: X → X +− X (2)

Пополним эту ФЗ: X →(X +− X)⋃ X, получится, что X → X + (3)

Теперь по первой аксиоме Армстронга из (1) имеем X +→ Y (4)

Значит, X → Y ∈ G +, по третьей аксиоме Армстронга, исходя из (3) и (4).

2)

Докажем обратное, что если X → Y ∈ G, то X → Y ∈ F +

По построению G имеем: Y = X +− X (5)

Для F имеем:

X → X + (по определению) (6)

X +→ X +− X (1 аксиома Армстронга, так как X +− X ⊆ X +) (7)

X → X +− X = Y (3 аксимома Армстронга из (6)и (7), и по равенству (5))

В итоге получили X → Y ∈ F +.

Теорема доказана.

Пример

УСО: R =(A, B, C)

Множество ФЗ: F =(A → B, B → A, C → A, A → C, B → C)

1)

G =(A → BC, B → AC, C → A)

2)

A += ABC, A +− A = BC

B += BAC, B +− B = AC

C += CAB, C +− C = AB

Тогда G =(A → BC, B → AC, C → AB) будет являться УНП.

Свойства "хорошей" схемы БД

"Хорошая", но не оптимальная. Должна обладать следующими свойствами:

• соединение без потерь;
• сохранение ФЗ;
• каждая схема отношений в этой БД находится в 3НФ. Наличие этого свойства обеспечивает отсутствие в схемах отношений следующих аномалий:
• избыточность;
• потенциальная противоречивсть;
• аномалия обновления;
• аномалия удаления.

Соединение без потерь

Чтобы схема БД обладала свойством соединения без потерь, необходимо, чтобы хотя бы одна из таблиц содержала ключ универсальной схемы отношений.

Пусть ρ =(R 1... R n) - схема БД. Она будет обладать свойством соединения без потерь, если для любого экземпляра отношения r из R справедливо равенство: r =Π R 1(r)⋈Π R 2(r)⋈...⋈Π R n (r), где Π R i (r) - это проекция экземпляра отношения r на множество атрибутов R i

Пример БД, не обладающей свойством соединения без потерь

R =(A, B, C)

ρ =(AB, BC)=(R 1, R 2)

F =(A → B)

Достаточно привести пример экземпляра r, для которого равенство не выполняется:

Полученное соединение не будет равняться r:

Этот пример показывает, что при неправильном построении БД запросы могут выдавать неправильный результат.

Пример БД, обладающей свойством соединения без потерь

R =(A, B, C)

ρ =(AB, AC)=(R 1, R 2)

F =(A → B)

Возьмём тот же экземпляр:

Полученное соединение будет равняться r:

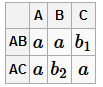
Но это не доказательство, а только один пример, просто чтобы показать, в чём разница.

Пример

Пусть R =(A, B, C)

ρ =(AB, AC)=(R 1, R 2)

F =(A → B)

Доказать, что ρ обладает свойством соединения без потерь.

1)

2)

Получили строку, сплошь состоящую из a. Значит ρ обладает свойством соединения без потерь.

Другой пример

Пусть R =(A, B, C, D, E, F, P, S)

ρ =(AB, ACDPS, BCPS, DEF)=(R 1, R 2, R 3, R 4)

F =(B → C, D → EF, B → PS, A → CDPS, AP → S)

Доказать, что ρ обладает свойством соединения без потерь.

1)

2)

первый просмотр:

второй просмотр:

Вот и получили строку, сплошь состоящую из a. Значит ρ обладает свойством соединения без потерь.

 

Соединение без потерь

Доказательство

1)

Получили строку, сплошь состоящую из a.

2)

Теперь докажем обратное, что если ρ обладает соединением без потерь, то имеет место одна из ФЗ: (1) или (2).

r =Π R 1(r)⋈Π R 2(r) (3)

r - это R 1⋃ R 2 (экземпляр универсальной схемы отношений)

Если выполняется равенство (3), то возможны два варианта:

1) b i ≠ b j, i ≠ j;

2) некоторые b i совпадают, b 1= b 2.

Тогда для выполнения равенства (3) необходимо, чтобы выполнялось одно из двух:

· a 1= a 2;

· c 1= c 2.

2 и 3 кортежи - лишние. Чтобы они не были лишними, они должны совпадать с одним из других кортежей, чтобы их можно было вычеркнуть.

Предположим, a 1= a 2, тогда что-то там насовпадало и 2 и 3 кортежи можно вычеркнуть.

Аналогичные рассуждения можно провести для случая, когда c 1= c 2, но тогда получаем:

· для варианта b i ≠ b j имеют место обе ФЗ: (1) и (2);

· для варианта с некоторыми совпадающими b i работает либо (1), либо (2).

Всё, теорема доказана.

Следствие из теоремы

Пусть R 1 и R 2 - это сущности БД и они связаны между собой. Тогда схема БД обладает соединением без потерь, если общий атрибут R 1 и R 2 содержит ключ одной из этих схем отношений.

R 1⋂ R 2= A

R 1− R 2= B

R 1⋂ R 2→ R 1− R 2, потому что A → B, так как является ключом.

Свойство сохранения ФЗ

Пусть дана схема БД ρ =(R 1... R n) и F - множество ФЗ.

Проекцией F на R i называется такое множество ФЗ, принадлежащее F +, что XY ⊆ R i, Π R i (F)

Схема ρ обладает свойством сохранения ФЗ, если:

(⋃ ni =1Π R i (F))+= F + - ФЗ могут быть декомпозированны по схеме отношений (тогда проверку надо будет выполнять только в рамках отдельных таблиц при включении новой записи).

Пример схемы БД без свойства сохранения ФЗ

R =(A, B, C) - универсальная схема отношений.

F =(A → B, B → C)

ρ =(AB, AC)=(R 1, R 2)

Надо доказать, что ρ не обладает свойством сохранения ФЗ.

Первая проекция: Π R 1(F)= F 1=(A → A, B → B, AB → A, AB → B, AB → AB, A → B, A → AB)

Вторая проекция: Π R 2(F)= F 2=(A → A, C → C, AC → A, AC → C, AC → AC, A → C, A → AC)

B → C ∈ F + по определению.

B → C ∉(F 1⋃ F 2)+ - не работает, так что эта БД не обладает свойством сохранения ФЗ.

B += B, C ∉ B +

Пример схемы БД со свойством сохранения ФЗ

R =(A, B, C) - универсальная схема отношений.

F =(A → B, B → C)

ρ =(AB, BC)=(R 1, R 2)

Надо доказать, что ρ обладает свойством сохранения ФЗ.

Первая проекция: Π R 1(F)= F 1=(тривиальные ФЗ, A → B, A → AB)

Вторая проекция: Π R 2(F)= F 2=(тривиальные ФЗ, B → C, B → BC)

(F 1⋃ F 2)+=(тривиальные ФЗ, A → B, A → AB, B → C, B → BC, A → C, A → AC), а это и есть по определению само F +, что и доказывает, что данная схема БД обладает свойством сохранения ФЗ.

Свойство сохранения ФЗ

Пример 1

Пусть R =(A, B, C), ρ =(AB, BC)=(R 1, R 2) и F =(A → B, B → C)

Обладает ли ρ сохранением ФЗ?

Смотрим:

1)

H =∅, УНП=(A → BC, B → C)

2)

G =(A → B, A → C, B → C)

3)

A → B, AB ⊆ R 1

A → C, AC ⊈ R 2, H =(A → C)

B → C, BC ⊆ R 2

4) пропускаем, так как не выполнилось условие в 3)

5)

H не пустое.

6)

выполняется ли A → C ∈(G − H)+=(A → B, B → C)+

A += ABC, C ∈ A +, значит ρ обладает сохранением ФЗ.

Пример 2

Пусть R =(A, B, C), ρ =(AB, AC)=(R 1, R 2) и F =(A → B, B → C)

Обладает ли ρ сохранением ФЗ?

1-4)

H =∅, УНП=(A → BC, B → C)

H =(B → C))

5)

H не пустое.

6)

выполняется ли B → C ∈(G − H)+=(A → BC)+

B += B, C ∉ B +, значит ρ не обладает сохранением ФЗ.

Ключ схемы отношения

Ключ схемы отношения – это подмножество исходной схемы, состоящая из одного или нескольких атрибутов, которые задают уникальность значений в кортежах отношений.

Если атрибут A i ∈ R входит в какой-либо ключ схемы отношения R, то он называется первичным. А если не входит ни в один, то называется непервичным.

Пусть

R =(A 1... A n) - некоторая схема отношения.

F - множество ФЗ.

Тогда

X ⊆ R называется ключом схемы, если выполняются:

· X → A 1... A n ∈ F +

· ∀ Z ⊂ X, Z → A 1... A n ∉ F +. То есть X содержит минимальное число атрибутов, для которых выполняется предыдущее свойство.

Алгоритм построения ключа

Базируется на определении ключа. Позволяет построить только один ключ.

1)

i =0, X 0= A 1... A n

2)

цикл по атрибутам A j в X i

Если (X i − A j)+= R, то X i +1= X i − A j, i = i +1 и выйти из цикла;

иначе продолжить цикл

3)

если i возросло, то перейти к шагу 2);

иначе X = X i - это найденный ключ.

Пример построения ключа

Пусть R =(A, B, C, D), F =(AB → DC, BC → AD)

Надо построить ключ.

1)

i =0, X 0= ABCD

2)

(X 0− A)+=(BCD)+= BCDA = R, значит X 1= BCD, i =1

3)

i, как видим, возросло, значит опять 2)

2)

(CD)+= CD ≠ R

(BD)+= BD ≠ R

(BC)+= BCAD = R, X 2= BC, i =2

3)

i, как видим, возросло, значит опять 2)

2)

C += C ≠ R

B += B ≠ R

3)

i, как видим, не возросло. Значит, X = BC - ключ. Но не единственный, X = AB - тоже ключ, просто у нас получился сначала этот.

Значит, A, B, C - первичные атрибуты, а D - непервичный.

Третья нормальная форма

Отношение находится в 3НФ, если не существует тройки:

• ключа X,
• Y ⊆ R,
• непервичного атрибута H ∉ Y,

для которой выполняются:

• X → Y ∈ F +;
• Y → H ∈ F +;
• Y → X ∉ F +.

Если такую тройку можно найти, то схема не находится в 3НФ.

Если схема отношения находится в 3НФ, то в большинстве случаев эта схема отношения не обладает аномалиями. Но существуют условия, когда схема в 3НФ обладает этими аномалиями. Хотя, встречаются они редко. Вот они:

• схема отношения имеет 2 или больше ключей,
• и любые 2 из них являются составными,
• и имеют общий атрибут.

Пример 1

Пусть R =(A, B, C, D), F =(A → B, AC → D) и ρ = R

Доказать, что это отношение не находится в 3НФ.

Доказываем:

1)

i =0, X 0= ABCD

2)

(BCD)+= BCD ≠ R

(ACD)+= ACDB = R, X = ACD, i =1

3)

i, как видим, возросло, значит опять 2)

2)

(CD)+= CD ≠ R

(AD)+= ADB ≠ R

(AC)+= ACBD = R, X 2= AC, i =2

3)

i, как видим, возросло, значит опять 2)

2)

C += C ≠ R

A += AB ≠ R

3)

i не возросло, значит X = X 2= AC - это ключ. Причём, можно показать, что он единственный.

Теперь предполагаем тройку:

• X = AC
• Y = A ⊆ R
• H = B - непервичный атрибут, B ∉ X

Проверям три условия для неё:

1)

X → Y, так как AC → A по 1 аксиоме Армстронга;

2)

Y → H, A → B по условию;

3)

Y ↛ X, A ↛ AC

A += AB, AC ⊈ A +

Таким образом, найдена тройка, для которой выполняются все три условия, а значит отношение не находится в 3НФ.

Пример 2

Декомпозируем эту схему отношения R на две схему отношений.

R =(A, B, C, D)

F =(A → B, AC → D)

ρ =(AB, ACD)=(R 1, R 2)

Если R 1 и R 2 находятся в 3НФ, то значит всё ρ будет в 3НФ.

Сначала покажем 3НФ у R 1=(AB), F =(A → B):

· X = A - выберем ключом

· Y, X → Y, Y ↛ X

Y = B, A → B, B ↛ A

· невозможно подобрать непервичный атрибут H ∉ Y, потому что непервичным может быть только B.

Таким образом, нельзя подобрать необходимую тройку. Значит, R 1 находится в 3НФ.

Теперь покажем 3НФ у R 2=(ACD), F =(AC → D):

· X = AC - выберем ключом

· Y, X → Y, Y ↛ X

а) A - что-то как-то не выполняется;

б) C - что-то как-то не выполняется;

в) D - что-то как-то не выполняется;

г) AD - что-то как-то не выполняется;

д) CD - что-то как-то не выполняется.

· H ∉ Y, H = D

а) Y = A, Y ↛ H

б) Y = C, Y ↛ H

в-д) H ∈ Y

Не удалось подобрать нужную тройку, так что R 2 тоже находится в 3НФ.

 

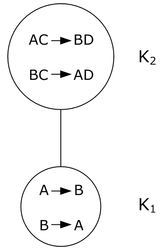
Третья нормальная форма

Пример аномалий у 3НФ

R =(A, B, C, D) и F =(A → B, B → A, AC → D)

Два ключа:

первый - AC:

(AC)+= ACBD = R

A += AB ≠ R

C += C ≠ R

второй - BC:

(BC)+= BCAD = R

B += BA ≠ R

Покажем, что в этом случае R находится в 3НФ:

1)

неключевой атрибут H, H = D

2)

Y → H, H ∉ Y, Y = AC

3)

X = BC, X = AC

Нельзя подобрать нужную тройку, потому R находится в 3НФ. Однако, отношение всё равно обладает аномалиями:

• избыточности: наименование поставщика повторяется для каждой поставляемой делали;
• противоречивости при изменении наименования поставщика надо изменить его во всех записях, куда оно входит;
• включения: нельзя включить информацию о поставщике, если он ничего не поставляет;
• удаления: при удалении детали удаляется информация о поставщике.

Для устранения этого вводится усиленная 3НФ - Бойса-Кодда.

Пример

U =(поставщик,фирма,деталь,количество)=(A, B, C, D)

F =(A → B, B → A, AC → D, BC → D)

Строим ρ:

1)

УНП=(A → B, B → A, AC → BD, BC → AD)

2)

пропускаем этот шаг, так как есть ФЗ (даже не одна), включающая все атрибуты из U

3)

уменьшить число атрибутов не удаётся

4)

1 класс: A → B, B → A, K 1= AB

2 класс: AC → BD, BC → AD, K 2= ABCD

5)

6)

для K 2:

способ 1 - как во втором семинаре

можно ли вывести AC → BD ∈(BC → AD)+?

(AC)+= AC, BD ⊈(AC)+, значит нельзя

можно ли вывести BC → AD ∈(AC → BD)+?

(BC)+= BC, AD ⊈(BC)+, значит нельзя

способ 2 - вычеркнуть из правых частей ФЗ рассматриваемых классов эквивалентностей общие атрибуты. Если получаются ФЗ с пустой правой частью, то они являются лишними.

AC → B

BC → A

выше по иерархии ничего нет, выбираем BC → AD

нет лишних ФЗ, потому...

 

Пример

7) редуцирование атрибутов справа ФЗ, расположенной по иерархии выше

вычёркиваем в графе A

8)

нет ФЗ с пустой правой частью, потому шаг пропускаем.

9)

ρ =(AB, BCD)=(R 1, R 2)

10)

проверяем

· соединение без потерь

F =(A → B, B → A, AC → D, BC → D)

Значит, ρ обладает сохранением без потерь.

· сохранение ФЗ

1-4)

H =∅, УНП=(A → B, B → A, AC → BD, BC → AD)

H =(AC → BD, BC → A)

5)

H ≠∅

6)

выполняется ли AC → BD ∈(A → B, B → A, BC → D)+?

(AC)+= ACBD, BD ⊂(AC)+

выполняется ли BC → A ∈(A → B, B → A, BC → D)+?

(BC)+= BCAD, A ⊂(BC)+

значит, ρ обладает сохранением ФЗ.

На практике, частно пренебрегают свойством сохранения ФЗ, если в БД вводятся правильные данные - не надо проверять, противоречат ли эти данные исходной ФЗ.

Таким образом, ρ обладает:

• обладает соединением без потерь;
• обладает сохранением ФЗ;
• точно находится в 3НФ.

Но мы всё равно проверим, находятся ли R 1 и R 2 в 3НФ Бойса-Кодда:

R 1= AB:

A → B, B → A

здесь A - ключ и B - ключ.

значит, находится в НФ.

R 2= BCD:

BC → D

BC - ключ.

значит, находится в НФ.

Преимущество

Алгоритм определяет стандартную (математическую) процедуру построения схемы БД.

Недостатки

• очень трудно определить всё множество ФЗ, а алгоритм критичен к набору этих ФЗ. В приципе, надо строить абстрактный экземпляр отношений (семинар №2), но надо знать и предметную область;
• при увеличении числа ФЗ возможно увеличение сложности вычисления алгоритма.

Эти недостатки сдерживают применение алгоритма на практике.

Нормальные формы

НФ

Отношение находится в 1НФ, если все его атрибуты атомарны, то есть ни один из его атрибутов нельзя разделить на более простые атрибуты, которые соответствуют каким-то другим свойствам описываемой сущности.

Также схема отношений находится в 1НФ, если не содержит таблицу или вектор в явном виде. Поэтому, если таблица скрыта в объекте, то схема будет в 1НФ.

Ясно, что отношение, находящееся в 1НФ, также может обладать избыточностью. Для её устранения предназначена вторая нормальная форма.

НФ

Отношение находится во второй нормальной форме (сокращённо 2НФ) тогда и только тогда, когда оно находится в первой нормальной форме и каждый его неключевой атрибут неприводимо зависим от первичного ключа.

Схема отношений находится в 2НФ, если не существует ключа X, подмножества атрибутов Y ⊂ X и непервичного атрибута H, для которых выполняются условия:

• X → Y;
• Y → H;
• Y ↛ X.

A 1→ A i... A j

X = A 1 A 2, Y = A 1⊂ X, H ∈(A i... A j):

1) X → Y, так как A 1 A 2→ A 1

2) Y → H, так как A 1→ A i... A j

3) Y ↛ X, так как A +1= A 1 A i... A j, X ⊈ Y +

НФ

Подробнее на лекции №5.

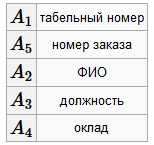
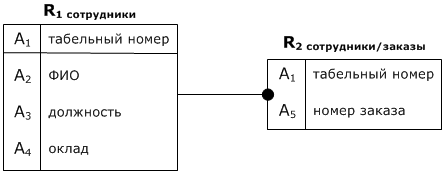
A 2→ A i... A j

X = A 1, Y = A 2, H ∈(A i... A j):

1) X → Y, так как A 1→ A 2

2) Y → H, так как A 2→ A i... A j

3) Y ↛ X, так как A +2= A 2 A i... A j, X = A 1∉ Y +

Пример 1

R - схема отношения "Сотрудники".

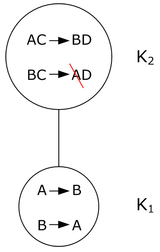
ФЗ:

A 1 A 5→ A 2 A 3 A 4

A 1→ A 2 A 3 A 4

A 3→ A 4

Покажем, что эта схема не находится в 2НФ:

Можно найти ключ X = A 1 A 5, Y = A 1⊂ X, H ∉ Y, H ∈(A 2, A 3, A 4):

1) X → Y

2) Y → H

3) Y ↛ X

R 1 тоже не находится во 2НФ, потому что X = A 1, Y = A 3, H = A 4:

1) X → Y

2) Y → H

3) Y ↛ X

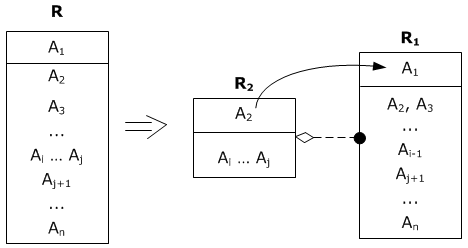
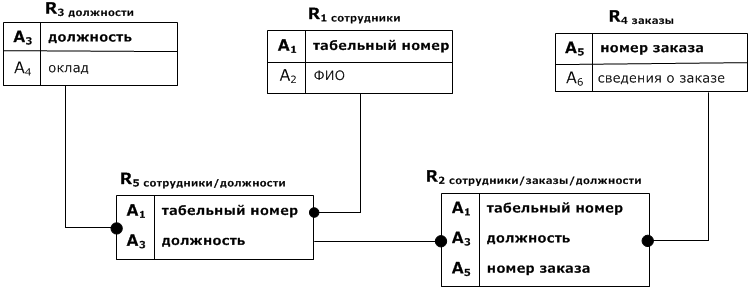
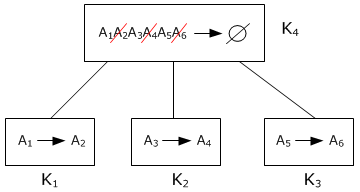
Предположим, вдруг оказалось, что сотрудник может занимать несколько должностей, и ещё теперь в таблице надо хранить сведения о заказе. В этом случае схема преобразуется к следующему виду:

Но анализ показывает, что в этом случае таблицы R 1 и R 2 не находятся в 2НФ:

R 1:

A 1→ A 2, X = A 1 A 3, Y = A 1⊂ X, H = A 2

1) X → Y, так как A 1 A 3→ A 1

2) Y → H, так как A 1→ A 2

3) Y ↛ X, так как Y += A 1 A 2, X ⊈ Y +

R 2:

A 5→ A 6, X = A 1 A 3 A 5, Y = A 5⊂ X, H = A 6

1) X → Y, так как A 1 A 3 A 5→ A 5

2) Y → H, так как A 5→ A 6

3) Y ↛ X, так как Y += A 5 A 6, X = A 1 A 3 A 5⊈ Y +

 

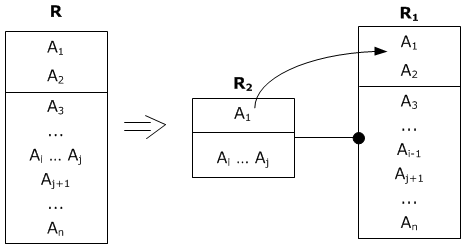
Пример 1

Поэтому вновь перестроим схему:

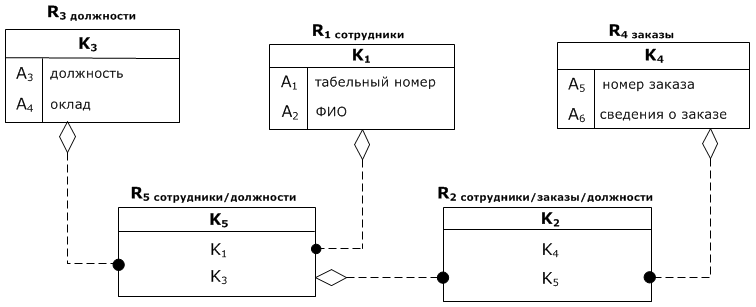
Указанная схема имеет два недостатка:

1. в ключи R 3, R 1 и R 4 входят атрибуты предметной области. При изменении формата табельного номера придётся обновить его в R 1 и через CASCADE в R 3 и R 4. Поэтому всегда желательно иметь синтетические ключи - не связанные с предметной областью (ID);
2. в сущностях R 2 и R 5 ключи составные. Это увеличивает размер индекса и время поиска по этому индексу.

В силу этого, схему БД предлагается реорганизовать следующим образом (ввести синтетические ключи):

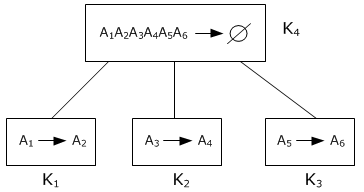
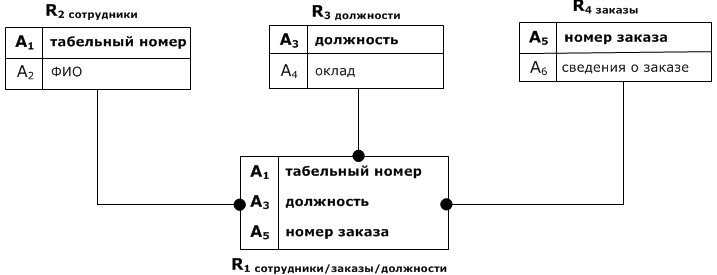
Пример 2

Разработать схему БД для предыдущего примера с применением алгоритма синтеза.

U = (табельный номер, ФИО, должность, оклад, номер заказа, сведения о заказе) = (A 1, A 2, A 3, A 4, A 5, A 6)

F =(A 1→ A 2, A 3→ A 4, A 5→ A 6)

Синтез:

1)

УНП=(A 1→ A 2, A 3→ A 4, A 5→ A 6)

2)

U →∅

в УНП нет ФЗ, включающей все атрибуты из U. Поэтому добавляем в УНП тривиальную ФЗ:

УНП=(A 1→ A 2, A 3→ A 4, A 5→ A 6, A 1 A 2 A 3 A 4 A 5 A 6→∅)

3)

все нетривиальные ФЗ в УНП являются неприводимыми (в левой части один атрибут). Поэтому шаг пропускаем.

4)

разбиваем УНП на классы ФЗ:

1. A 1→ A 2, K 1= A 1 A 2
2. A 3→ A 4, K 2= A 3 A 4
3. A 5→ A 6, K 3= A 5 A 6
4. A 1 A 2 A 3 A 4 A 5 A 6→∅, K 4= A 1 A 2 A 3 A 4 A 5 A 6

5)

строим граф иерархии:

6)

пропускаем, так как в каждом классе только одна ФЗ.

7)

выполняем редуцирование атрибутов ФЗ:

8)

пропускаем, так как в графе иерархии нет ФЗ, кроме U →∅

9)

ρ =(A 1 A 3 A 5, A 1 A 2, A 3 A 4, A 5 A 6)

10)

1) соединение без потерь

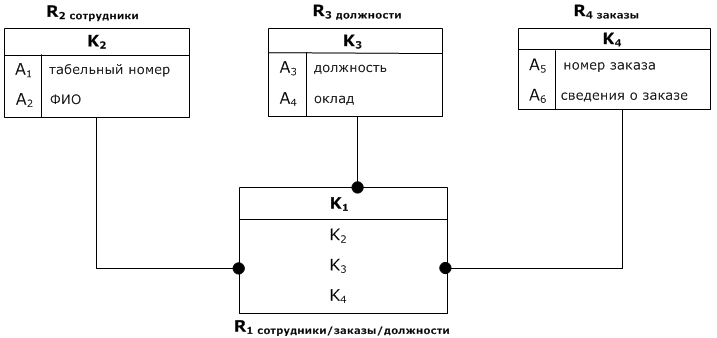
Получили строку, сплошь состоящую из a. Значит, есть соединение без потерь. Запрос на соединение всех четырёх таблиц будет выполняться правильно.

2) сохранение ФЗ:

1-4) H =∅, УНП=(A 1→ A 2, A 3→ A 4, A 5→ A 6)

5) H - пусто.

6) обладает сохранением ФЗ. При включении новой записи в таблицу достаточно проверять справедливость тех ФЗ, которые связаны с этой таблицей.

3) каждая схема отношения находится в 3НФ. Вот так.

А находятся ли схемы отношений R 1, R 2, R 3, R 4 в нормальной форме Бойса-Кодда?

R 1:

R 1= A 1 A 3 A 5, A 1 A 3 A 5 - ключ, значит находится в НФБК.

R 2:

R 2= A 1 A 2, A 1→ A 2, A 1 - ключ, значит находится в НФБК.

R 3:

R 4= A 3 A 4, A 3→ A 4, A 3 - ключ, значит находится в НФБК.

R 4:

R 4= A 5 A 6, A 5→ A 6, A 5 - ключ, значит находится в НФБК.

В конце концов, получаем такую схему БД:

Но у неё тоже есть недостатки:

1. ключ в R 1 составной;
2. в ключах R 2, R 3, R 4 используются атрибуты предметной области.

Перестроим схему с синтетическими ключами:

Сравнивая результаты Примера 1 и Примера 2, видим, что алгоритм синтеза даёт меньшее число схем отношений.

 

Оптимизация SQL-запросов

Запрос, поступающий в СУБД, подвергается оптимизации с целью уменьшения времени его выполнения.

Шаги оптимизатора:

1. строится логический план выполнения запроса (дерево логических операций);
2. на основе логического плана строится физический план выполнения запроса (дерево физических операций);
3. реализация этого физического плана.

Законы реляционной алгебры

Закон каскада проекций

Допустим, (a 1... a n)⊆(b 1... b n), a i, b i - это атрибуты отношения R

тогда Π a 1... a n (Π b 1... b n (R))=Π a 1... a n (R)

Закон каскада селекций

Допустим, F = f 1∧ f 2

тогда σ F (R)= σ f 1(σ f 2(R))

Оптимизация SQL-запросов

Логический план

Лекция №11 - Оценки

 

Оптимизация SQL-запросов

Физический план

Пример

Допустим, T (R)=1000, I (R, a)=5, I (R, b)=10, I (R, c)=2, где a, b, c - положительные натуральные числа.

И f =(a <3 OR b ≥5) AND c =2

Найти T (Q).

Обозначим:

• a <3 как F 1;
• b ≥5 как F 2;
• f =(a <3 ORb ≥5) как F 3;
• c =2 как F 4.

1)

F 1⋃ F 2= F 3

p 3= p 1+ p 2− p 1⋅ p 2=25+610−25⋅610=0.76

2)

f = F 3⋂