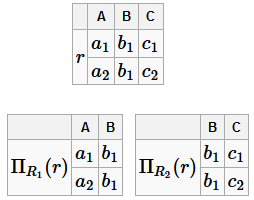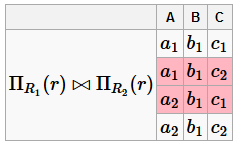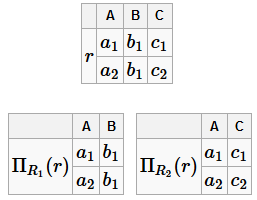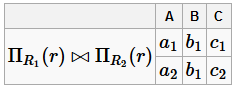Замыкание множества функциональных зависимостей

Пусть R - универсальная схема отношения, а F - исходное множество функциональных зависимостей на этой схеме. Замыканием F называется всё множество функциональных зависимостей, которое логически следует из F - обозначается как F +

Функциональная зависимость логически следует из F, если её можно вывести (получить) с помощью аксиом Армстронга.

Аксиомы Армстронга

Или правила вывода функциональной зависимости. Существуют различные интерпретации аксиом, но все эквивалентны. Потому приведём только один вариант.

Аксиомы Армстронга являются надёжными и полными.

Надёжность - если ФЗ выводится с помощью аксиом Армстронга, то она справедлива во всех экземплярах отношения, где справедливы исходные ФЗ F

Полнота - если имеет место какая-либо ФЗ, то она обязательно может быть выведена с помощью аксиом Армстронга.

Рефлексивность

Если Y ⊆ X ⊆ R

то X → Y. Тривиальная аксиома.

Дополнение

Если X → Y и Z ⊆ R (Z может быть пустым),

тогда X ⋃ Z → Y ⋃ Z или XZ → YZ

Транзитивность

Если X → Y, а Y → Z,

то X → Z

Пример построения множества ФЗ

Пусть задана УСО (универсальная схема отношения) R =(A, B, C) и зависимости F =(A → B, B → C)

1. A → A, B → B, C → C, AB → A, AB → B, AC → A, AC → C, BC → B, BC → C, ABC → A, ABC → C, AB → AB, AC → AC, BC → BC, ABC → AB, ABC → AC, ABC → BC, ABC → ABC
2. A → AB (1ФЗ и пополняем A), AC → BC, B → BC (2 ФЗ и пополняем B), AB → AC, AC → ABC, AB → ABC, AB → BC, A → AC
3. A → C (1 и 2 ФЗ), A → ABC

Всё, замыкание (F +) построено. Все перечисленные зависимости образуют замыкание.

Лемма

Справедливы следующие правила. Для их доказательства необходимо пополнить ФЗ так, чтобы можно было использовать аксиомы.

Правило объединения

Если X → Y и X → Z, то X → YZ

Доказательство:

1. X → XY (1 ФЗ и пополняем X);
2. XY → YZ (2 ФЗ и пополняем Y);
3. X → YZ (по аксиоме транзитивности).

Правило декомпозиции

Если X → Y, а Z ⊆ Y, то X → Z

Доказательство:

1. X → Y (по условию);
2. Y → Z (по аксиоме рефлексивности);
3. X → Z (по аксиоме транзитивности).

Правило псевдотранзитивности

Если X → Y и WY → Z, то WX → Z

Доказательство:

1. WX → WY (1 ФЗ и пополняем W);
2. WY → Z (по условию);
3. WX → Z (по аксиоме транзитивности).

Замыкание множества атрибутов

Замыкание F + может включать в себя очень большое количество ФЗ. Например:

F =(X → A 1, X → A 2... X → A n)

X → Y ⊆ F +

Y ⊆(A 1, A 2... A n) и таких подмножеств может быть 2 n

Поэтому "в лоб" замыкание F + никто не строит. Но необходимо найти какой-то метод, который достаточно просто позволял бы выяснять, принадлежит ли произвольная ФЗ X → Y к F +

Для этого применяется замыкание множества атрибутов.

Пусть R - универсальная схема отношения, а X - некоторое подмножество атрибутов. Тогда замыканием множества атрибутов X + называется совокупность атрибутов A i 1, A i 2... A ik таких, что X → A i 1, X → A i 2... X → A ik

Алгоритм построения

Алгоритм является итерационной процедурой.

1. полагаем i =0 и X +0= X, а X + i - замыкание множества атрибутов на i-том шаге;
2. X + i +1= X + i ⋃ V, где V - такое множество атрибутов в F, что существует ФЗ Y → Z, где Y ⊆ X + i, V ⊆ Z;
3. если X + i +1= X + i, то X += X + i, иначе i = i +1 и возвращаемся в пункт 2.

Пример построения

Пусть R =(A, B, C, D, E, G)

F =(AB → C, C → A, BC → D, ACD → B, D → EG, BE → C, CG → BD, CE → AG)

X = BD

Надо построить X +:

1) i =0, X +0= BD

2)

Получили, что X +4= X +3, а значит X += X +3= BDEGCA

Это означает, что имеют место следующие ФЗ: BD → B, BD → D, BD → E, BD → G, BD → C, BD → A, и все они ⊆ F +

Короче, чтобы проверить X → Y ⊆ F +, необходимо построить X +

 

Лекция №3 - Хорошая схема БД - Соединение без потерь

Пусть F и G - два множества ФЗ.

G называется покрытием F, если имеет место равенство G += F +

Существуют различные виды покрытий. Но мы рассмотрим только один - условно-неизбыточное покрытие.

Алгоритм построения условно-неизбыточного покрытия

1) если в множестве ФЗ F встречаются ФЗ с одинаковой левой частью X, то следует объединить эти ФЗ в одну ФЗ. Это следует из леммы объединения. Получившееся множество ФЗ обозначим G;

2) для каждой ФЗ X → Y из G заменить её на X → X +− X;

После выполнения 1) и 2) получаем замыкание G += F +

Доказательство

1)

Докажем, что если ФЗ X → Y ∈ F (из этого следует, что Y ⊆ X + (1) по определению замыкания множества аттрибутов), то эта ФЗ принадежит G +

По построению G имеет место ФЗ: X → X +− X (2)

Пополним эту ФЗ: X →(X +− X)⋃ X, получится, что X → X + (3)

Теперь по первой аксиоме Армстронга из (1) имеем X +→ Y (4)

Значит, X → Y ∈ G +, по третьей аксиоме Армстронга, исходя из (3) и (4).

2)

Докажем обратное, что если X → Y ∈ G, то X → Y ∈ F +

По построению G имеем: Y = X +− X (5)

Для F имеем:

X → X + (по определению) (6)

X +→ X +− X (1 аксиома Армстронга, так как X +− X ⊆ X +) (7)

X → X +− X = Y (3 аксимома Армстронга из (6)и (7), и по равенству (5))

В итоге получили X → Y ∈ F +.

Теорема доказана.

Пример

УСО: R =(A, B, C)

Множество ФЗ: F =(A → B, B → A, C → A, A → C, B → C)

1)

G =(A → BC, B → AC, C → A)

2)

A += ABC, A +− A = BC

B += BAC, B +− B = AC

C += CAB, C +− C = AB

Тогда G =(A → BC, B → AC, C → AB) будет являться УНП.

Свойства "хорошей" схемы БД

"Хорошая", но не оптимальная. Должна обладать следующими свойствами:

• соединение без потерь;
• сохранение ФЗ;
• каждая схема отношений в этой БД находится в 3НФ. Наличие этого свойства обеспечивает отсутствие в схемах отношений следующих аномалий:
• избыточность;
• потенциальная противоречивсть;
• аномалия обновления;
• аномалия удаления.

Соединение без потерь

Чтобы схема БД обладала свойством соединения без потерь, необходимо, чтобы хотя бы одна из таблиц содержала ключ универсальной схемы отношений.

Пусть ρ =(R 1... R n) - схема БД. Она будет обладать свойством соединения без потерь, если для любого экземпляра отношения r из R справедливо равенство: r =Π R 1(r)⋈Π R 2(r)⋈...⋈Π R n (r), где Π R i (r) - это проекция экземпляра отношения r на множество атрибутов R i

Пример БД, не обладающей свойством соединения без потерь

R =(A, B, C)

ρ =(AB, BC)=(R 1, R 2)

F =(A → B)

Достаточно привести пример экземпляра r, для которого равенство не выполняется:

Полученное соединение не будет равняться r:

Этот пример показывает, что при неправильном построении БД запросы могут выдавать неправильный результат.

Пример БД, обладающей свойством соединения без потерь

R =(A, B, C)

ρ =(AB, AC)=(R 1, R 2)

F =(A → B)

Возьмём тот же экземпляр:

Полученное соединение будет равняться r:

Но это не доказательство, а только один пример, просто чтобы показать, в чём разница.