
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Размерно-массовая модель аэростатного зондаСодержание книги
Поиск на нашем сайте
Геометрические характеристики АЗ, такие как характерный размер, характерная площадь, форма остаются постоянными во время спуска в атмосфере. Геометрические характеристики аэростатной оболочки являются функцией выпущенного в оболочку газа, его температуры и давления, избыточного давления, жесткостной характеристики оболочки, потерь газа в результате диффузии и утечек. Представление размерно-массовых характеристик базируется на условии выполнения аэростата
где
Для выполнения аэростата с растяжимой оболочкой полагается линейная зависимость объема аэростата
где b – коэффициент, учитывающий жесткостные характеристики оболочки. Его значение определялось по данным эксперимента
Предполагается, что невыполненный аэростат имеет сферическую форму, а его объем определяется из первого уравнения системы при DP = 0. Масса подъемного газа
где
При проведении проектных расчетов по продолжительности дрейфа АЗ целесообразно разделить утечки и диффузию подъемного газа через материал оболочки, так как механизм их действия различен.
Тепловая модель аэростата Движение АЗ при выходе на высоту дрейфа и в свободном дрейфе в атмосфере существенно зависит от теплообмена между подъемным газом и внешней средой, так как температура и давление газа в аэростатной оболочке определяют объем и, следовательно, аэростатическую силу аэростата. Математическое описание реальных тепловых процессов, имеющих место при свободном дрейфе аэростата, – достаточно сложная задача. Для ее упрощения в данной тепловой модели приняты следующие допущения и предположения: · распределение температур оболочки аэростата и стенки баллона высокого давления по поверхности и толщине оболочки и стенки баллона принято равномерным;
· параметры состояния подъемного газа в оболочке аэростата · истечение подъемного газа через диафрагму при наполнении является адиабатическим, потери тепла в трубопроводе наполнения отсутствуют, и подъемный газ на входе в оболочку имеет температуру газа в баллонах высокого давления; · изменение внутренней энергии подъемного газа в баллонах высокого давления происходит за счет работы и массообмена дросселирования (при наполнении), а также за счет теплообмена свободной конвекцией со стенками баллонов; · изменение внутренней энергии баллонов высокого давления · изменение внутренней энергии подъемного газа в оболочке аэростата происходит за счет работы и массообмена дросселирования (при наполнении и потерях газа в процессе дрейфа), теплообмена свободной конвекцией с оболочкой аэростата и работы атмосферы по сжатию (расширению) подъемного газа; · подъемный газ считается полностью оптически прозрачным для всех видов излучения, а его собственное излучение отсутствует; · изменение внутренней энергии оболочки аэростата осуществляется за счет теплообмена свободной конвекцией с подъемным газом внутри оболочки, конвекцией с окружающей средой, а также за счет излучения атмосферы и поверхности планеты и собственного излучения оболочки. С учетом этого тепловой режим аэростата описывается следующими уравнениями:
Коэффициент теплоотдачи при свободной конвекции – функция числа Релея R а:
Коэффициент теплоотдачи при вынужденной конвекции – функция числа Рейнольдса Rе:
Аэродинамическая модель Аэродинамическая сила является равнодействующей сил давления и трения, возникающих при движении аппарата относительно воздушной среды. В общем случае она зависит от формы, размеров, компоновки аппарата, плотности среды, ее вязкости и скорости звука, величины и ориентации вектора воздушной скорости, скорости вращения относительно центра масс и т.д. В проекциях на оси скоростной системы координат с учетом допущения о плоском движении полная аэродинамическая сила дает следующие составляющие:
В случае совместного торможения нескольких устройств, как, например, АЗ, парашюта и аэростата, их действие считается независимым и может быть представлено следующим образом:
На участке спуска аэростата аэродинамические характеристики представляются аэродинамическими характеристиками сферической (венерианской) оболочки аэростата. При проведении расчетов по дрейфу аэростатной станции рассматривалась только одна составляющая полной аэродинамической силы – сила лобового сопротивления. Так как форма аэростата сильно влияет на аэродинамические силы, то для их определения использовался поправочный коэффициент
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.174.186 (0.008 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

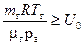 ,
,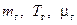 – масса, температура и молекулярная масса рабочего тела (подъемного газа);
– масса, температура и молекулярная масса рабочего тела (подъемного газа);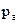 – давление атмосферы;
– давление атмосферы;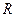 – универсальная газовая постоянная.
– универсальная газовая постоянная.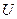 от избыточного давления
от избыточного давления 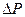 , текущие значения которых определяются из решения следующей системы уравнений:
, текущие значения которых определяются из решения следующей системы уравнений: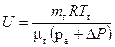 ,
,
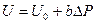 ,
,
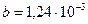 м3/Па.
м3/Па.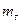 в аэростате является линейной функцией времени,
в аэростате является линейной функцией времени, 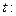
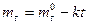 ,
,
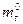 – начальная масса подъемного газа;
– начальная масса подъемного газа;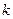 – экспериментальный коэффициент потерь подъемного газа в результате диффузии и утечек.
– экспериментальный коэффициент потерь подъемного газа в результате диффузии и утечек.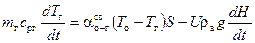 ,
,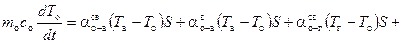
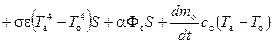 ,
,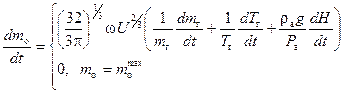
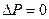 ,
,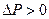 ,
,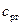
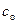
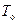
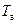

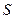
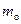
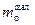
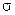
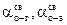
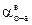
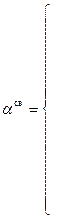
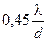
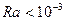 ,
,
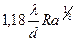
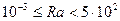 ,
,
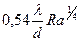
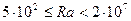 ,
,
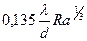
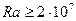 .
.
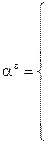
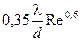
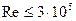 ,
,
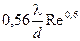
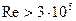 ,
,
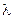
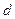
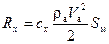 ,
, 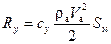 ,
,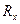
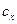
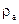
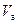
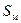
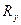
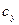
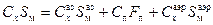
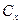
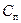
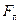
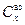
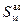
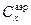
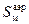
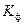 , зависящий от степени наполнения оболочки:
, зависящий от степени наполнения оболочки: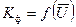 , где:
, где:  .
.


