
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы сопротивления движению автомобиля
Сопротивление движению автомобиля складывается из следующих сил: 1. Сопротивление качению колес – Pf. 2. Сопротивление подъема – Ph. 3. Инерции автомобиля – Рj 4. Сопротивление воздуха – Pw.
Сопротивление качению колес на дороге с уклоном может быть определено с помощью рис. 34, где показано разложение вектора Рис. 34. Разложение вектора силы тяжести силы тяжести автомобиля по автомобиля по двум направлениям на две плоскости: параллель- ную дороги и перепендику- лярную к ней. Сила сопротивления качению колес автомобиля на подъеме равна: Рf = Ga cos a × f, где Ga cos a – проекция вектора силы тяжести на плоскость, перпендикулярную поверхности дороги. Сопротивления подъема Рh есть проекция вектора силы тяжести автомобиля на плоскость, параллельную дорожной поверхности: Рh = Ga sin a. Общее сопротивление дороги на подъеме равно Рy = Рf + Рh, что можно записать как Рy = Gа ×(f cos a + sin a) = Gа ×y, (17) где y – коэффициент обшего дорожного сопротивления. Сила инерции автомобиля Рj складывается из следующих составляющих Рj = Рja + Рjk + Рjд, (26) где Рj – сила инерции автомобиля; Рjk – сила инерции колес автомоюиля; Рjд – приведенная сила инерции вращающихся деталей двигателя. Pj = где SJk – сумма моментов инерции колес; SJе – сумма моментов инерции вращающихся деталей двигателя; dwk/dt – угловое ускорение колес; dwe/dt – угловое ускорение деталей двигателя; итр – передаточное чтисло трансмиссии; hтр – кпд трансмиссии. Остальные обозначения использовались ранее. Исходя из того, что V = w×r, (где V – окружная скорость; w – угловая скорость; r – радиус колеса), в уравнение (27) вместо dwк /dt и dwе /dt подставляем выражения
dwк /dt = dV/dt ×1/rк и dwк /dt = dwе /dt × итр = dV/dt × итр/rк, получим Pj = = Выражение в скобках обозначим d. Оно называется к о э ф ф и ц и е н т о м у ч е т а в р а щ а ю щ и х с я м а с с автомобиля. Сила инерции автомобиля с использованием этого коэффициента может быть определена: Pj = Коэффициент учета вращающихся масс находится обычно по эмпирической зависимости, предложенной акад. Чудаковым Е.А. [ ]. d = 1 + 0,03...0,05 + 0,04 икп2 × ирк2, (29) где икп – передаточное число передачи в коробке передач; ирк – передаточное число передачи в раздаточной коробке. Численное значение коэффициента учета вращающихся масс d на первой передаче в коробке передач и низшей передаче в раздаточной коробке полноприводных автомобилей достигает 6,5...7, а неполноприводных, в которых отсутствует раздаточная коробка, d = 1,7...2,5. На последней передаче в коробке передач и высшей передаче в раздаточной коробке d = 1,06...1,13. Сопротивление воздуха является основной силой сопротивления для автомобиля, движущегося с высокой скоростью. При скорости 80...90 км/ч сопротивление воздуха для легковых автомобилей становится равным сопротивлению качению колес на горизонтальной асфальтированной дороге, а далее – значительно превышает его. Близкие к этим величинам показатели и грузовых автомобилей. Снижению сопротивления воздуха поэтому уделяется большое внимание особенно для легковых автомобилей, скорости которых, как правило, значительно выше 90 км/ч.. Сопротивление воздуха движению тела в диапазоне скоростей от 1 м/с до 330 м/с (скорость звука) зависит от скорости в квадрате, а при скорости выше звуковой – в кубе. Т.е. для реальных скоростей автомобиля зависимость силы сопротивление воздуха от скорости – квадратичная: Рw = где Рw – сила сопротивление воздуха, Н; К – коэффициент сопротивления воздуха, Н×с2 /м4; F – наибольшая поперечная (лобовая) площадь автомобиля, м2; V– скорость автомобиля, км/ч.
Приближенно лобовую площадь F можно определить по следующим зависимостям: для грузовых – F = B ×H, для легковых – F = 0,78 B1×Н, где B – колея автомобиля. Самое малое сопротивление воздуха имеет падающая капля воды, её наибольшая площадь сечения находится на расстоянии 1/3 от преднего конца. Численные значения К и F приведены в табл. 6. Таблица 6
. Лобовая площадь равна: ВАЗ-2106 – 1,74 м2, М-2141 – 1,887 м2, ГАЗ-3110 – 2,277 м2, Газель – 3,25 м2, ГАЗ-52 – 3,3 м2, ГАЗ-53 – 3,84 м2, ЗИЛ-130 – 4,9 м2, КАМАЗ-5320 – 6,85 м2, МАЗ-5335 – 6,4 м2, ЛИАЗ-677 – 6,53 м2. С учетом угла натекания на автомобиль воздушного потока, силы действия потока по направлениям осей координат, исходящим из центра тяжести автомобиля, определяются как [10]: Рw = Сx × Под углом натекания воздушного потока в плоскости, параллельной плоскости дороги, понимается угол между направлением движения автомобиля и геометрической суммой скорости воздушного потока и скорости движения автомобиля. То же в вертикальной плоскости называется углом атаки. Обычно угол натекания не более 30о. Кроме продольной силы от воздушного потока на автомобиль действует также боковая Ру и подъемная Рz силы. При этом боковая сила оценивается коэффициентом боковой силы Сy, подъемная сила – коэффициентом подъемной силы Сz. Коэффициент полной аэродинамической силы Сw равен ____________ Cw = Ö Cx2+ Cy2 + Cz2. (20) Наибольшее значение для практической оценки влияния сопротивления воздуха имеет коэффициент Cx, который обычно используется для xарактеристики обтекаемости автомобиля, равен: Cx = где К – коэффициент сопротивления воздуха. Выражение q = Полная аэродинамическая сила может быть найдена по выражению Рw = Cw × F ×q. (22) Тогда Сx = Значения коэффициентов Сx автомобилей: ВАЗ-2106 – 0,509; ВАЗ-2108 и ВАЗ-2109 – 0,38; ЗАЗ-1102 – 0,37; М-2141 – 0,478; ГАЗ-24 – 0,48; ГАЗ-33029 – 0,413; ГАЗ-13 – 0,502; РАФ-2203 – 0,439; ПАЗ-652 – 0,376; ЛИАЗ-677 – 0,734; ГАЗ-53 – 0,965; ЗИЛ-130 – 0,805; КАМАЗ-5320 – 0,673; МАЗ-5335 – 0,75. Атомиобиль с хорошо отработанной формой кузова Мерседес кл. Е имеет Сx= 0.27… 0,29. Для легковых спортивных автомобилей Сx= 0,14...0,2, например, Форд Проба – 0,14, Мицубиси ХСР – 0,2. Наиболее обтекаемую форму имеет падающая капля, для неё Сх = 0,05..
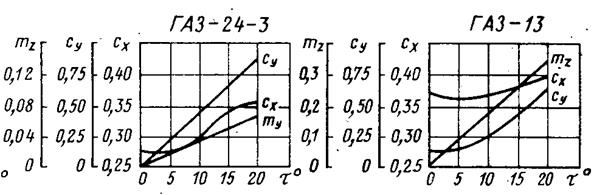
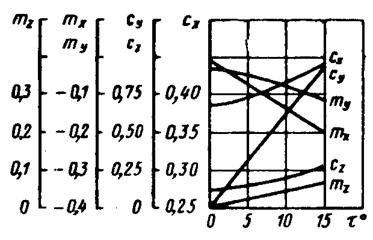
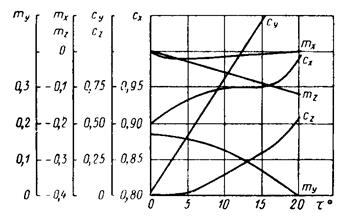
Действующий под углом натекания воздушный поток вызывает поворот автомобиля вокруг осей X, У, Z. Практическое значение имеет лишь поворот вокруг оси Z, который влияет на курсовую устойчивость автомобиля. Действие момента вокруг оси Z оценивается коэффициентом поворачивающего момента. Поворачивающие автомобиль моменты вокруг осей Z, Х и У определяются Мz = mz × q × F × B, Мx = mx ×q ×F×B и My = my ×q ×F ×L , (23) где mх, my, mz – коэффициенты поворачивающего момента вокруг осей Z, Х и У; q – скоростной напор; F – лобовая площадь; B – ширина автомобиля, L – длина автомобиля. Зависимость коэффициентов Сх, Су Сz и mх, my, mz в от угла натекания воздушного потока показаны на рис. 35, 36, 37 Рис. 35. Зависимость коэффициентов Сx, Cy, Сz и mz от угла натекания воздушного потока t о для легковых автомобилей ГАЗ-24-3 и ГАЗ-13
Рис. 36. Зависимость коэффициентов Сx, Cy, Сz и mх, my, mz от угла натекания воздушного потока t о для грузового автомобиля ЗИЛ-130
Рис. 37. Зависимость коэффициентов Сx, Cy, Сz и mх, my, mх от угла натекания воздушного потока t о для автобуса ПАЗ-652 Полный аэродинамический момент Mw выражается Мw = mw ×q ×F × B, где mw – коэффициент полного аэродинамического момента. Он определяется ___________________ mw = Ö mx2 + (my × B/L + mz2). (24) Численные значения поворачивающего момента, подъемной силы и лобового cопротивления при скорости 100 км/ч и угле натекания 20o автомобилей ГАЗ-21 и ГАЗ-24 "Волга" приведены в табл. 5. Таблица 7
Приведенные сопротиления воздуха определялись на уровне моря. На высоте в горных районах сопротивление снижается. Так мощность сопротивления воздуха движению автомобиля ГАЗ-24 при скорости 80 км/ч на уровне моря равно 8 л.с., а на высоте 2500 м – 5,5 л.с. С целью снижения сопротивления воздуха форма кузова легкового автомобиля тщательно отрабатывается в специальном устройстве – аэродинамической трубе, где воздушный поток создается с помощью вентиляторов. Чтобы расход электроэнергии на привод вентиляторов был минимальный, труба делается замкнутой.
Испытания в аэродинамической трубе ведутся на автомобилях в натуральную величину или на уменьшенных моделях с сохранением критерия подобия – числа Рейнольдса R = где L – длина автомобиля; L1 – длина модели; V – скорость воздушного потока при испытаниях автомобиля; V1 – скорость воздушного потока при испытаниях модели; r – плотность воздуха (1,22 кг/м3); m – коэффициент вязкости воздуха (1,82 ×10–6 кг×с/м при давлении 760 мм ртутного столба и 18o C, ГОСТ 4401-81); r 1 и m1 – плотность и коэффициент вязкости воздуха при испытаниях модели. Если r и m принять без изменений, то V×L = V1×L1. Таким образом, чем меньше длина модели, тем больше должна быть скорость воздушного потока.
Силы, движущие автомобиль На спуске движущией автомобиль силой является проекция вектора силы тяжести на плоскость, параллельную дороге: Рh = Ga sin a, (30) где Рh – движущая сила на спуске; Ga – вес автомобиля; a – угол спуска. На подъме эта сила является тормозящей (было показано на рис. 31). При движении с замедлением движущей является также сила инерции автомобиля. Определить окружную силу на ведущих колесах можно, если известны характеристика двигателя, передаточные числа агрегатов трансмиссии и динамический радиус колеса: Рo = где Рo – окружная сила; Мe – крутящий момент двигателя; итр – передаточное число трансмиссии; rd – динамический радиус колеса; hтр – кпд трансмисии автомобиля. итр = икп × ирк × игп, (31)
Аналогично кпд трансмиссии автомобиля hтр = hкп × hрк × hгп. На рис. 38 показана внешняя скоростная характеристика поршневого двигателя. Nе – мощность двигателя, кВт; Mе – крутящий момент двигателя, Н×м; q – удельный часовой расход топлива, г/кВт×ч; nе – частота вращения коленчатого вала двигателя, об/мин
Рис. 38. Внешняя скоростная характеристика двигателя Внешней характеристика называется потому, что она получается при полной подаче топлива в цилиндры двигателя и на графике протекает выше остальных, называемых частичными характеристиками, которые получаются при меньшей (частичной) подаче топлива. Изменение мощности двигателя и крутящего момента при полной и частичной подачах топлива в % показано на рис. 39.
Рис. 39. Изменение мощности двигателя и крутящего момента двигателя в зависимости от количества подаваемого топлива
Частота вращения коленчатого вала при максимальном крутящем моменте для бензиновых двигателей равна примерно 0,5 частоты, при которой развивается максимальная мощность двигателя. Максимальный крутящий момент дизелей – при более высокой частоте.
Если известно максимальное значение мощности двигателя и частота вращения коленчатого вала двигателя, то значение мощности при других частотах можно найти по следующей эмпирической зависимости [4]. Nе = Nеmax × где Ne– мощность при заданной частоте вращения коленчатого вала; Nеmax – максимальная мощность двигателя; a, b и c – коэффициенты (для карбюраторных двигателей равны 1, для четырехтактных дизелей: а = 0,53, b = 1,56, c = 1,09); ne – частота вращения коленчатого вала, при которой определяется значение мощности двигателя; nNmax – частота вращения коленчатого вала при максимальной мощности. Отклонения рассчитанной по выражению (32) мощности от реальной, замеренной на стенде, достигают 10...15%. Значения крутящего момента двигателя, если известна мощность, можно определить по выражению, H×м: Mе = 9550 × Отношение значения максимального крутящего момента двигателя Me к значению крутящего момента при максимальной мощности MNmax называется к о э ф ф и ц и е н т о м п р и с п о с а б л и в а е м о с т и двигателя e =
Для карбюраторных двигателей e = 1,05...1,15, для дизелей e =,15...1,35. Желательно, чтобы коэффициент приспосабливаемости был по возможности выше. Это делает управление автомобилем легче, т.к. сокращается количество переключений передач в тяжелых дорожных условиях. При равномерном движении автомобиля, если известно значение крутящего момента его двигателя, сила тяги на ведущих колесах может быть определена по выражению Рт =
где Рт – сила тяги на ведущих колесах автомобиля; hтр – кпд трансмиссии автомобиля; Ga – вес автомобиля; f – коэффициент сопротивления качению колес автомобиля. Кпд т р а н с м и с с и и двухосного автомобиля с одной ведущей осью имеет максимальное значение, 0,92...0,94. Кпд трансмиссии полноприводных многоосных автомобилей – 0,75...0,85. Каждая пара шестерен трансмиссии снижает кпд: цилиндрическая, хорошо изготовленная и приработанная – на 1...2%, не приработанная – на 2...2,5%, коническая пара соответственно – на 2...4% и 3...4%. Поэтому количество пар шестерен, передающих крутящий момент в трансмиссии автомобиля, должно быть по возможности меньше. Кпд шарнира карданной передачи в зависимости от угла равен: 50 – 0,999; 100 – 0,988; 150 – 0,932; 180 – 0,87. Особенно сильно уменьшается кпд при низкой температуре, когда смазка в агрегатах загустевает. Так, при 30оС кпд трансмиссии автомобиля ГАЗ-53 равен 0,9, при 15оС – 0,8, при 0оС – 0,65. При температуре минус 20...25оС летние смазки увеличивают момент трения в 5...6 раз по сравнению с моментом трения при +15оС, а при температуре минус 50оС кпд трансмиссии близок к нулю. Если в агрегатах трансмиссии при минус 50о залита летняя, а не зимняя или арктическая смазка, то без предварительного разогрева трансмиссии автомобиль не может тронуться с места. С увеличением частоты вращения шестерен и валов кпд агрегата уменьшается, а при увеличении передаваемого крутящего момента повышается. Состояние трансмиссии и ходовой части автомобиля обычно определяется длиной свободного качения (выбега) до остановки на горизонтальной дороге при скорости 50 км/ч. Длина свободного качения не менее: ВАЗ-2105 – 500 м, М-2140 – 420 м, ГАЗ-24 – 650 м, УАЗ-469 – 400 м, ГАЗ-66 – 400 м, ЗИЛ-130 – 600 м, ЗИЛ-131 – 400 м, ГАЗ-53А – 550 м, Урал-375Д – 600 м. Кпд ш и н ы при ее качении по дорожной поверхности можно определить как hш = 1 – f, где f – коэффициент сопротивления качкемию еолеса.
1.8. Выбор передаточных чисел агрегатов трансмиссии Главная передача Выбор передаточных чисел агрегатов трансмиссии автомобиля начинается с передаточного числа главной передачи. При этом исходят из условия обеспечения возможности движения с требуемой максимальной скоростью при включенной последней передаче в коробке передач и высшей передаче в раздаточной коробке. Максимальная скорость в км/ч может быть определена: Vmax = где rк – радиус качения колеса, м; ne – частота вращения коленчатого вала, об/мин; икп, ирк , игп – передаточные числа соответственно коробки передач, раздаточной коробки и главглй передачи. Отсюда передаточное число главной передачи равно: игп = 0,377× Если раздаточной коробки на автомобьле нет, при расчете в привеленных формулах ставится 1. В зависимости от условий эксплуатации и требуемой максимальной скорости для одной базовой модели автомобиля могут изготавливаться несколько главных передач. Так, на автомобиле ЗИЛ-130 главная передача имеет передаточное число 6,32. На выполненном на его базе самосвале ЗИЛ-ММЗ-555 передаточное число главной передачи равно 6,97. Аналогично на автомобиле МАЗ-500: главная передача имеет передаточное число 7,73, самосвала на его базе – 9,57. Коробка передач До 70...80 % пути автомобили проходят на последней передаче в коробке передач. Поэтому на заднеприводных автомобилях последняя передача делается прямой, т.к. кпд на этой передаче наиболее высокий. На переднееприводных легковых автомобилях с поперечным расположением двигателя и двухвальными коробками передач (ВАЗ-2108, ВАЗ-2109, ВАЗ-2110 и др.) прямая передача в коробке передач отсутствует. Если по условиям движения наибольший пробег совершается на предпоследней передаче, например, тяжелые грузовики, прямой делается предпоследняя передача. Например, уставливавшейся на автомобилях УРАЛ-375, -377, ЯАЗ-210, МАЗ-200 в коробке передач ЯМЗ-204У. передаточное число последней пятой передачи равно 0,78. В коробке передач ЯМЗ, уставливаемой на автомобилях МАЗ-5335, КРАЗ-255,-260 передаточное число последней передачи равно 0,66. На автомобиле УРАЛ-4320 передаточное число последней передачи в коробке передач – 0,723. При включенной в коробке передач первой передаче на колесах автомобиля должна развиваться максимальная сила тяги. Поэтому передаточное число первой передачи наибольшее. Ограничивается оно буксованием колес на сухой твердой дороге при полной загрузке автомобиля или необходимостью преодоления сопротивления дороги с коэффициентом общего дорожного сопротивления y = 0,27...0,33 (большее значение берется для грузовых автомобилей). Сила тяги, содаваемая ведущими колесами, должна быть больше или равна силе сопротивления движению автомобиля, но меньше или равна максимальной силе сцепления ведущих колес с дорогой: Рj ³ РТ1 ³ Рy, где Pj – максимальная сила сцепления ведущих колес; PТ1 – сила тяги на колесах при включенной в коробке передач первой передаче; Py – сила сопротивления движению автомобиля. В развернутом виде это выражение можно записать:
Gсц ×j ³
где Ме – крутящий момент двигателя; и1 – передаточное число первой передачи в коробке передач; Gсц – сцепной вес автомобиля (вес, приходящийся на ведущие колеса); hтр – кпд трансмиссии; rd – динамический радиус колеса. Остальные обозначения использовались ранее. Передаточное число первой передачи из последнего выражения можно записать: Gсц ×j ×rd Gа ×y ×rd ¾¾¾¾¾ ³ и1 ³ ¾¾¾¾ (53) Me × игп ×hтр Me ×игп × hтр Определенные по этим условиям передаточные числа первой передачи оказываются близкими по своим значениям. Для дальнейших расчетов из определенных этих двух значений принимается наименьшее передаточное число. Отношения передаточного числа первой передачи (и1) в коробке передач к последней (иn) называется передаточным диапазоном коробки передач. Передаточный диапазон коробок передач легковых автомобилей равен 2,8...4, грузовых – 5,5...8,5, автобусов – 3...5. Разбивка передаточного диапазона с целью получения передаточных чисел промежуточных передач производится из условия получения наилучших разгонных качеств на каждой промежуточной передаче. Максимальная мощность двигателя развивается при высокой частоте вращения коленчатого вала. При разгоне автомобиля после включения следующей передачи частота вращения коленчатого вала снижается, поэтому снижается и мощность двигателя. Чтобы мощность оставалась достаточно высокой, частота вращения коленчатого вала после включения следующей передачи не должна уменьшаться на большую величину. Это обеспечивается соответствующим подбором передаточных чисел в коробке передач. На рис. 40 показаны зависимости изменения мощности Ne и скорости V автомобиля от частоты вращения коленчатого вала n1 после включения передач. Так как высокое значение мощности двигателя находится в диапазоне частоты вращения коленчатого вала от n1 до n2, в этом диапазоне и должен работать двигатель при разгоне автомобиля после включения каждой из последующих передач.
Рис. 40. Изменение мощности двигателя и скорости при разгоне автомобиля Зависимость мощности двигателя и скорости автомобиля от частоты вращения коленчатого вала в диапазоне от n1 до n2 при различных передачах в коробке передач показана на рис. 40 в виде ломаной линии. Выбор передаточных чисел промежуточных передач коробки передач делается из условия, что. максимальная скорость V1max автомобиля на первой передаче будет при частоте вращения коленчатого вала n2 (рис. 40). После включения второй передачи скорость автомобиля сохраняется, но будет минимальной для второй передачи – V2min. Равенство скоростей V1max = V2min можно выразить как V1max = 0,377× Приравняв правые части этих выражений, после сокращений запишем
где и1 – передаточное число первой передачи в коробке передач; и2 – передаточное число второй передачи в коробке передач; n1 – минимальная частота вращения коленчатого вала после включения передачи (показно на рис. 40); n2 – максимальная частота вращения коленчатого вала Аналогичное отношение можно составить для третьей, четвертой, пятой передач: где q – знаменатель геометрической прогрессии; n – номер последней передачи в коробке передачи; n-1 – номер предпоследней передачи. Таким образом, чтобы иметь хорошие разгонные качества автомобиля, передаточные числа в передаточном диапазоне коробки передач должны распределяться по закону г е о м е т р и ч е с к о й прогрессии: и2 = и1 ×q; и3 = и2 ×q = и1×g2; и4 = и3 ×q = и1 ×q3… иn = и1 ×qn–1 , т.е. для любой m –ной промежуточной передачи иm= и1 × qm–1 . Для коробки передач с последней прямой передачей иn = 1, и1×qn –1 = 1. Из последнего выражения знаменатель геометрической прогрессии n – 1______ q = Ö 1 / и1 (54) Передаточное число промежуточной передачи иm = Если прямой передачей в коробке передач является предпоследняя, можно записать n – 2 _____ иn –1 = и1 × qn –2 = 1; q = Ö 1/ и1. Передаточное число промежуточной передачи для такой коробки n–2 ______ иm = и1 × qm –1 = Ö и1n – m+1, (56) Распределение передаточных чисел промежуточных передач по закону геометрической прогрессии (геометрическому ряду) в передаточном диапазоне коробкок передач колесных и гусеничных транспортных машин используется довольно часто. Но известны и другие способы разбивки передаточного диапазона, например, по гармоническому ряду, по арифметическому ряду, по гиперболическому ряду и т.д. Г а р м о н и ч е с к и й ряд характеризуется постоянной разностью обратных величин соседних чисел – q:
Если иn = 1, то иn –1 = Из последнего выражения знаменатель гармонического ряда q = где n – число передач в коробке передач вместе с последней прямой. В коробках передач, передаточный диапазон разбит по гармоническому ряду, знаменатель q = 0,2...0,3. Передаточное число любой промежуточной передачи при разивке по за гармоническому ряду будет иm = где m – номер передачи. Для а р и ф м е т и ч е с к о г о ряда свойственно постоянство разности соседних передаточных чисел коробки передач – q: и1 – и2 = q; и2 – и3 = q; и3 – и4 = q; иn-1 – иn = q. Если иn = 1, то иn –1 = q +1, иn –2 = 2q + 1; иn –3 = 3q + 1 и т.д. Откуда q = где n – число передач вместе с последней прямой. Знаменатель арифметической прогрессии передаточных чисел передач q = 1,5...1,7. Передаточное число любой промежуточной передачи при разбивке по арифметическому ряду может быть определено по выражению иm = В табл. 6 приведены расчетные значения передаточных чисел для коробки передач легкового автомобиля полной массой 1340 кг, номинальной мощностью двигателя 59 кВт, определенные в НАМИ по законам указанных рядов.
Таблица 8 Передаточные числа коробки передач
Как видно в табл. 8, при разбивке передаточного диапазона по арифметическому ряду передаточные числа второй и третьей передач выше, чем при разбивке по другим рядам. Следовательно, сила тяги на этих передачах больше и разгон будет интенсивней. При разбивке по гармоническому ряду ниже будет расход расход топлива на этих передачах. Поэтому ряды эти соответственно называются силовой и экономичный. Геометрический ряд дает промежуточные значения. С целью экономии топлива передаточный диапазон коробок передач легковых автомобилей в последние годы чаще разбивается по закону гармонического ряда. В реальных коробках передач знаменатель прогрессии для высших передач несколько снижается. Разрыв между передаточными числами высших передач уменьшается из-за того, что при высоких скоростях сопротивление движению сильно возрастает и мощности двигателя после вкючения следующей передачи не хватает, чтобы интенсивно разгонять автомобиль. Отношение передаточных чисел коробок передач некоторых отечественных автомобилей приведены в табл. 9. Таблица 9
По г и п е р б о л и ч е с к о м у ряду передаточные числа промежуточных передач определяются с помощью выражения nm = Передаточное число задней передачи в коробке передач делается близким по значению к передаточному числу первой передачи насколько позволяет конструкция коробки передач. Количество передач с ростом скоростей автомобилей увеличивается. На ранних моделях легковых автомобилей (“Победа”, “Волга” ГАЗ-21, “Москвич” -400,-401) устанавливались механические коробки передач с 3-мя передачами, на более поздних моделях – с 4-мя, а в последние годы – с 5-ью, 6-ью передачами. В автоматических коробках передач нередко бывает и 7 передач. Последняя передача в коробках передач легковых автомобилях часто имеет передаточное число меньше единицы. Максимальная скорость на этой передаче может быть достигнута только, если автомобиль загружен частично. При полной загрузке указанная в технической характеристи
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.26.176 (0.148 с.) |
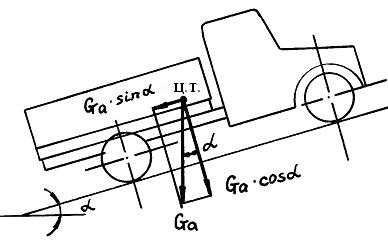 Сопротивление качению колес автомобиля может быть найдено путем сложения сопротивлений качению всех его колес или умножением веса автомобиля на коэффициент сопротивления качению f. Значения f для различных дорог приведены в табл. 2.
Сопротивление качению колес автомобиля может быть найдено путем сложения сопротивлений качению всех его колес или умножением веса автомобиля на коэффициент сопротивления качению f. Значения f для различных дорог приведены в табл. 2.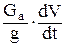 +
+  , (27)
, (27)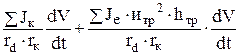 =
=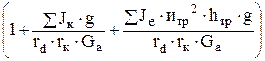 . (28)
. (28)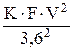 , (18)
, (18)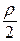 × F ×V2, (19) где Сx – коэффициент лобового сопротивления, величина безразмерная; r –плотность воздуха (1,25 кг/м3 при давлении 760 мм ртутного столба и 18оС, ГОСТ 4401-81).
× F ×V2, (19) где Сx – коэффициент лобового сопротивления, величина безразмерная; r –плотность воздуха (1,25 кг/м3 при давлении 760 мм ртутного столба и 18оС, ГОСТ 4401-81).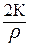 = 1,63К,
= 1,63К,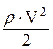 . (21)
. (21)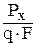 ; Cy =
; Cy = 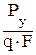 ; Сz =
; Сz = 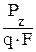 .
.
 =
= 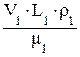 , (25)
, (25)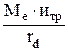 × hтр,
× hтр,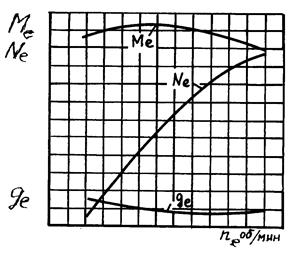 где икп – передаточное число коробки передач; ирк – передаточное число раздаточной коробки; игп – передаточное число главной передачи.
где икп – передаточное число коробки передач; ирк – передаточное число раздаточной коробки; игп – передаточное число главной передачи.
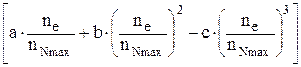 , (32)
, (32)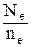 . (33)
. (33) .
. – Gа× f,
– Gа× f,

 , (51)
, (51)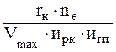 .
. 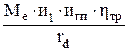 ³ Ga ×y, (52)
³ Ga ×y, (52)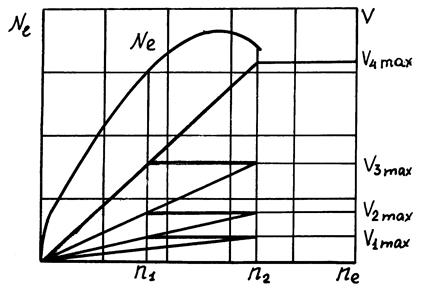 Разгон начинается на первой передаче. Когда частота вращения коленчатого вала достигнет n2, водитель включит вторую передачу. Частота при этом снизится до значения n1. На второй передаче разгон автомобиля вновь происходит до частоты n2, после чего включается третья передача и частота опять упадет до n1. т.д. до максимальной скорости на последней передаче..
Разгон начинается на первой передаче. Когда частота вращения коленчатого вала достигнет n2, водитель включит вторую передачу. Частота при этом снизится до значения n1. На второй передаче разгон автомобиля вновь происходит до частоты n2, после чего включается третья передача и частота опять упадет до n1. т.д. до максимальной скорости на последней передаче..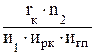 ; V2min = 0,377×
; V2min = 0,377× 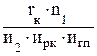 .
.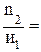
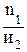 или
или  ,
,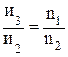 ;
; 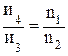 ;
; 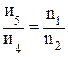 и т.д. Следовательно,
и т.д. Следовательно,

 …
…  q,
q,  . (55)
. (55)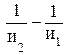 = q;
= q; 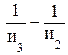 = q;
= q;  = q;
= q;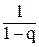 ; иn -2 =
; иn -2 =  ; иn -3 =
; иn -3 =  ; иn - 4 =
; иn - 4 = 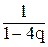 .
.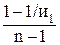 , (57)
, (57)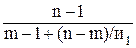 , (58)
, (58)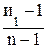 , (59)
, (59)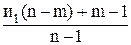 . (60)
. (60) .. (61)
.. (61)


