
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение квадратичной формы к каноническому виду. Метод Лагранжа.Содержание книги
Поиск на нашем сайте Канонический вид квадратичной квадратичной формы – вид, в котором отсутствуют слагаемые с парными произведениями переменных Любую квадратичную форму можно привести к каноническому виду: – форму двух переменных – трёх переменных … – форму И ключевой момент этой технической стороны состоит в линейных заменах: Систему часто записывают в виде компактного матричного уравнения Пример 6 Привести квадратичную форму к каноническому виду методом Лагранжа. Записать матрицу соответствующего линейного преобразования.
Решение: здесь используются стандартные замены
Запишем матрицу проведённого линейного преобразования: Ответ: Пример, конечно, прозрачный, но сразу зададимся вопросом – как выполнить проверку? Её можно выполнить матричным методом по формуле В нашем случае Пример 7 Привести квадратичную форму к каноническому виду методом Лагранжа. Записать матрицу соответствующего линейного преобразования. Решение: когда в форме присутствуют квадраты переменных (а они есть почти всегда), то используется другой приём. Идея состоит в выделении полных квадратов по формулам Сначала выбираем какую-нибудь переменную, которая находится в квадрате, здесь можно выбрать «двойку» удобно вынести за скобки: очевидно, всё дело сведётся к формуле выделяем полный квадрат: Теперь проведём замены
И тут вроде бы можно записать матрицу линейного преобразования, но есть одна загвоздка, проведённые замены имеют вид
|
||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

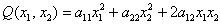 – к виду
– к виду 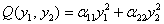
 – к виду
– к виду 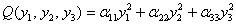 ;
;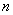 переменных
переменных 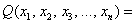 – к виду:
– к виду: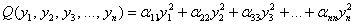
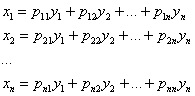 – ТАКИХ, которые как раз и приводят форму к каноническому виду.
– ТАКИХ, которые как раз и приводят форму к каноническому виду. , где:
, где: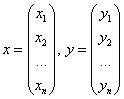 – столбцы старых и новых переменных,
– столбцы старых и новых переменных,  – матрица линейного преобразования.
– матрица линейного преобразования.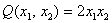
 с последующим применением формулы
с последующим применением формулы 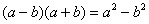 :
: – форма
– форма 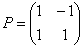 – она состоит из «игрековых» коэффициентов замен
– она состоит из «игрековых» коэффициентов замен 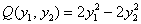 ,
,  , где
, где 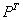 – транспонированная матрица линейного преобразования,
– транспонированная матрица линейного преобразования,  – исходная и
– исходная и 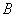 – новая матрица квадратичной формы.
– новая матрица квадратичной формы.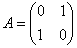 – исходная матрица формы
– исходная матрица формы 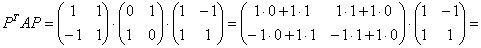
 – получаем матрицу формы
– получаем матрицу формы 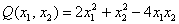
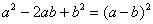 ,
, 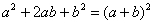 с дальнейшей заменой переменных.
с дальнейшей заменой переменных.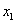 или
или 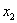 . Переменные традиционно перебирают по порядку, поэтому рассматриваем
. Переменные традиционно перебирают по порядку, поэтому рассматриваем 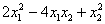
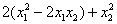
 и, чтобы ничего не изменилось – за скобками проводим вычитание:
и, чтобы ничего не изменилось – за скобками проводим вычитание: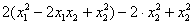
 , после чего выполним проверку обратными действиями – раскроем скобки и приведём подобные слагаемые:
, после чего выполним проверку обратными действиями – раскроем скобки и приведём подобные слагаемые: , ОК
, ОК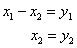 :
: – форма
– форма 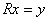 :
: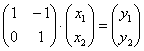
 уравнения
уравнения 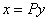 .
.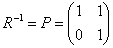 Для разрешения уравнения
Для разрешения уравнения 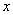 умножим обе его части на
умножим обе его части на 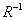 слева:
слева:
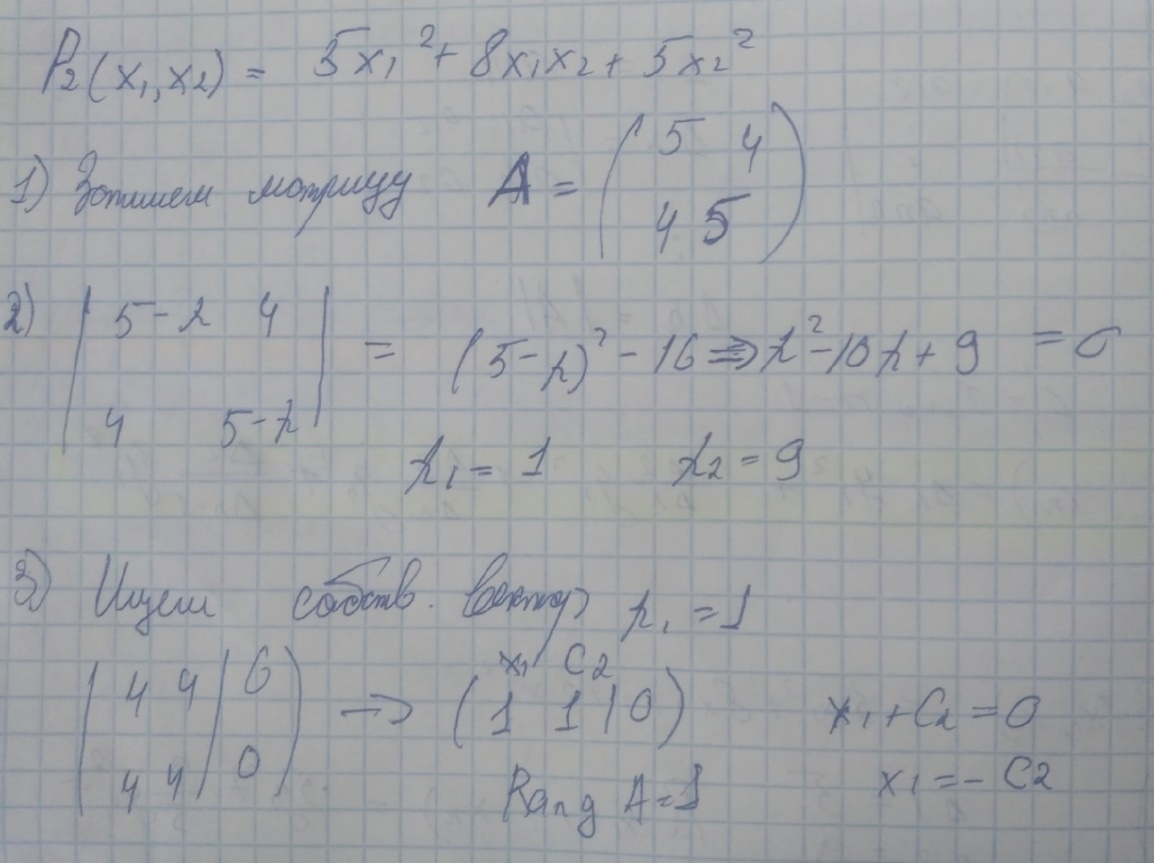 Метод ортогональных преобразований:
Метод ортогональных преобразований:



