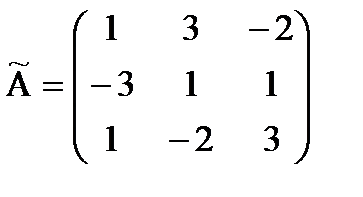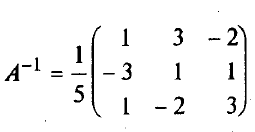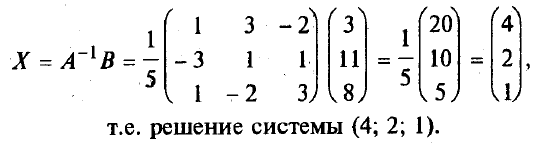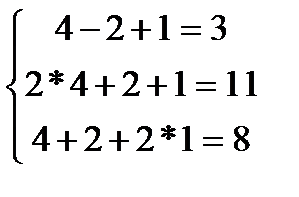Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Билет №4 .Системы линейных уравнений. Матричная запись систем линейных уравнений. Правило Крамера. Метод Гаусса. Решение матричных уравнений и линейных систем с помощью обратной матрицы.Содержание книги
Поиск на нашем сайте
Системы линейных уравнений Система m линейных уравнений с n переменными в общем виде записывается следующим образом:
где xj – переменные, aij, bi – константы, При этом величины aij (те константы, которые умножаются на переменные) принято называть коэффициентами при переменных, а правые части уравнений bi (те константы, которые не умножаются на переменные) - свободными членами. Более кратко ту же систему можно записать в виде:
Решением такой системы называют совокупность n числовых значений переменных xj, при подстановке которых в систему каждое уравнение обращается в истинное равенство.
Систему уравнений называют совместной, если она имеет хотя бы одно решение (т.е. хотя бы один такой набор из n чисел), и несовместной, если она не имеет решений.
Совместную систему уравнений называют определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.
Кроме того, для решения систем линейных уравнений используют также понятие расширенной матрицы системы, которую получают, приписав к матрице системы справа столбец свободных членов:
Элементарным преобразованиям строк матрицы: · а) отбрасыванию нулевых строк; · б) умножению всех элементов строки на число, отличное от нуля; · в) изменению порядка строк; · г) прибавлению к каждому элементу строки соответствующих элементов другой строки, умноженных на любое число. Таким образом, применяя к системе уравнений элементарные преобразования строк, мы получим равносильную систему. Методы решения систем линейных уравнений Рассмотрим вначале случай, когда число уравнений равно числу переменных, т.е. m = n. Тогда матрица системы - квадратная, а ее определитель называют определителем системы.
Метод обратной матрицы Рассмотрим в общем виде систему уравнений АХ = В с невырожденной квадратной матрицей А. В этом случае существует обратная матрица А-1. Домножим слева обе части на А-1. Получим А-1АХ = А-1В. Отсюда ЕХ = А-1В и Х = А-1В. Последнее равенство представляет собой матричную формулу для нахождения решения таких систем уравнений. Использование этой формулы получило название метода обратной матрицы
Например, решим этим методом следующую систему:
В конце решения системы можно сделать проверку, подставив найденные значения в уравнения системы. При этом они должны обратиться в верные равенства. Для рассмотренного примера проведем проверку:
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.167.85 (0.01 с.) |

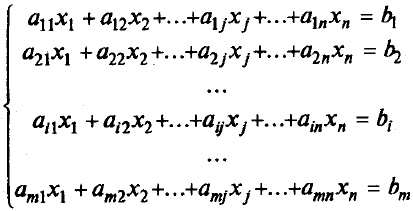
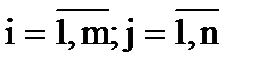 .
.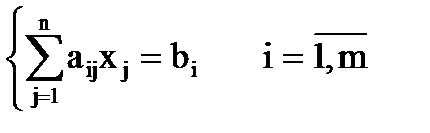
 Запишем систему линейных уравнений в общем виде в матричной форме. Обозначим:
Запишем систему линейных уравнений в общем виде в матричной форме. Обозначим:

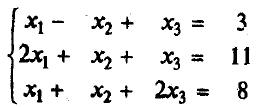
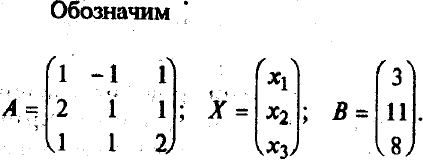

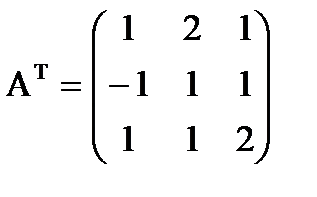 ;
;