Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нейтральные электромагниты постоянного тока
Ток подается в обмотку ЭМ, которая создает магнитный поток. При этом ЭМ притягивает якорь, механически связанный с каким-либо устройством (клапаном, заслонкой, золотником, контактной системой и т. д.). В ЭМ имеются воздушные зазоры 5 и 6. Их количество и форма зависят от конструкции ЭМ. Воздушный зазор 5, в котором возникает полезная сила, называется рабочим. Поверхности подвижной и неподвижной частей магнитопровода, ограничивающие рабочий воздушный зазор, называют полюсами.
В зависимости от конструктивного исполнения различают нейтральные ЭМ с внешним притягивающимся якорем (рис. 5.2, а), с втягивающимся якорем – соленоидные (рис. 5,2, б) и с внешним поперечно движущимся якорем (рис. 5.2, в). ЭМ с внешним притягивающимся якорем применяются при сравнительно небольших рабочих ходах якоря. ЭМ с втягивающимся якорем имеют плоские или усеченные конические полюса (говорят: «плоский стоп» или «конический стоп»). Они отличаются большим ходом якоря. ЭМ с внешним поперечно движущимся якорем позволяют получать вращательное движение. Тяговые и механические характеристики. При подаче тока в обмотку ЭМ возникает электромагнитная сила, под действием которой якорь притягивается к сердечнику, преодолевая сопротивление механических сил. Зависимость электромагнитной силы от величины рабочего воздушного зазора называется тяговой характеристикой ЭМ. Зависимость противодействующих механических сил, приведенных к точке приложения электромагнитной силы, от величины рабочего воздушного зазора называется механической характеристикой ЭМ. Найдем выражение для электромагнитной силы. При подключении обмотки ЭМ с постоянным воздушным зазором к источнику напряжения питания уравнение электрической цепи имеет вид:
где U – напряжение источника питания; i – ток обмотки; R – активное сопротивление обмотки; Ψ – потокосцепление обмотки. Умножив выражение (5.1) почленно на idt,получим уравнение энергетического баланса
Левая часть этого уравнения определяет количество электрической энергии dWe, поступающей из сети в ЭМ за время dt. Первый член правой части – потери энергии dW а в активном сопротивлении обмотки за время dt. Второй член правой части – электрическая энергия dW м, преобразованная в энергию магнитного поля при изменении потокосцепления за время dt. Интегрируем (5.2) на интервале от 0 до t:
Выражение (5.3) – тот же закон сохранения энергии, но уже интегральный, за все время процесса. Потокосцепление и ток связаны уравнением Ψ = f (i, δ), включающим в себя координату δ, характеризующую положение якоря и определяющую магнитное сопротивление ЭМ. Таким образом, электрическая энергия источника питания преобразуется в тепловую энергию потерь и энергию магнитного поля ЭМ. При неподвижном якоре преобразования электрической энергии в механическую не происходит. Энергию магнитного поля в соответствии с (5.3) можно определить из кривой намагничивания ЭМ для фиксированной величины воздушного зазора (рис. 5.3, а). Энергия магнитного поля пропорциональна заштрихованной площади, заключенной между кривой намагничивания Ψ = Ψ(i) и осью ординат. При ненасыщенным магнитопроводе и большом воздушном зазоре напряженность магнитного поля воздушного зазора значительно превосходит напряженность магнитного поля магнитопровода, поэтому энергия магнитного поля ЭМ в основном сосредоточена в воздушном зазоре. Рассмотрим процессы, происходящие при срабатывании ЭМ. На рис. 5.3, б показаны две кривые намагничивания, соответствующие исходному положению якоря с зазором δн (кривая 0 а)и притянутому положению якоря с зазором δк (кривая 0 с). При достижении потокосцеплением значения Ψ1 начинается процесс движения якоря. Энергия магнитного поля, преобразованная из электрической энергии источника питания за время от момента подключения обмотки до начала движения якоря,
пропорциональна площади 0 а b 0.
При токе i 1 начинается движение якоря. Характер изменения потокосцепления от тока характеризуется кривой ат. После окончания движения якоря потокосцепление достигает значения Ψ2. При движении якоря электрическая энергия преобразуется в энергию магнитного поля, пропорциональную площади b ате b. В точке m движение якоря прекращается, но так как ток еще не достиг установившегося значения I y, то потокосцепление продолжает нарастать по кривой намагничивания для притянутого положения якоря, достигая установившегося значения Ψy. Изменение потокосцепления при притянутом якоре сопровождается приращением энергии магнитного поля, пропорциональным площади етс d е. В целом приращение энергии магнитного поля пропорционально заштрихованной площади. Если бы ток I y подавался в обмотку при притянутом положении якоря, то энергия магнитного поля при токе I y соответствовала бы площади 0 тс d 0. Как видно, энергия магнитного поля, оставшаяся в ЭМ, меньше полученной энергии. Разность энергий, пропорциональная площади 0 ат 0, преобразована в механическую энергию движения якоря. Из-за нелинейности кривых намагничивания и нелинейного изменения тока при движении якоря определение энергии магнитного поля, преобразуемой в механическую энергию, связано с большими трудностями. При вычислении механической энергии примем следующие допущения: 1) кривые намагничивания имеют линейный характер (что соответствует ненасыщенному магнитопроводу); 2) поток рассеяния незначителен; 3) ток обмотки при движении якоря остается неизменным. С учетом принятых допущений графическое изображение энергии магнитного поля принимает вид, показанный на рис. 5.4.
Из выражения (5.4) следует, что при движении якоря половина энергии, потребляемой от источника, преобразуется в механическую энергию, а половина идет на пополнение энергии магнитного поля (площадь 0 am 0 равна половине площади bameb). Определим силу тяги ЭМ. Из ТОЭ известно, что механическая сила, возникающая в магнитном поле, равна производной от энергии магнитного поля по координате, которую стремится изменить сила. Под действием электромагнитной силы система контуров с токами стремится занять положение, соответствующее максимуму потокосцеплений. В случае одного контура с током электромагнитная сила стремится так изменить контур, чтобы его индуктивность увеличилась. В нашем случае
где х – перемещение якоря; d х = – dδ. Минус отражает, что с ростом x значение воздушного зазора δ уменьшается. Величину dW м находим дифференцированием (5.4), для чего заменяем Ψ2 на текущее Ψ. Результат подставляем в (5.5):
Находим магнитный поток. Пренебрегаем магнитным сопротивлением магнитопровода и нерабочих воздушных зазоров, а также потоком рассеяния, то есть принимаем, что вся энергия магнитного поля сосредоточена в воздушном зазоре. При этом в классической формуле Hl = Iw в роли l выступает δ.
Тогда выражение для электромагнитной силы принимает вид:
Если в (5.7) выразить Iw через Ф, и далее Ф через BS, получим формулу
известную как формула Максвелла. Она входит во все учебники по электрическим аппаратам и удобна для расчетов, когда направление движения якоря совпадает с направлением поля. Теоретически при уменьшении зазора P э → ¥. В действительности с учетом магнитного сопротивления магнитопровода P э имеет конечное значение. Значительное увеличение P э при уменьшении зазора может привести к явлению залипания якоря, при котором якорь остается в притянутом состоянии после отключения тока обмотки вследствие остаточного намагничивания магнитопровода. В электромагнитных реле для предотвращения явления залипания на якоре имеется немагнитная прокладка – штифт отлипания. На рис. 5.5 помимо тяговой характеристики ЭМ с плоскопараллельными полюсами приведены тяговые характеристики соленоидного ЭМ без внешнего магнитопровода (кривая 2) и с внешним магнитопроводом (кривая 3). Как видно из кривой 3, соленоидные ЭМ с внешним магнитопроводом имеют мало изменяющуюся тяговую характеристику в широком диапазоне хода якоря. Характер перемещения якоря ЭМ зависит от соотношения тяговой и механической характеристик электромагнита. Механическая характеристика – это зависимость силы механического сопротивления Р мех от перемещения якоря δ.
На рис. 5.6 приведены механические характеристики различных видов нагрузки ЭМ. Обозначения: δ н – начальный зазор, δ к конечный зазор. Рисунок а) – нагрузка в виде поднимаемого груза. Сила сопротивления не зависит от δ, а определяется весом груза и передаточным числом. Рисунок б) – растягивающая пружина. Усилие линейно зависит от δ. На рисунке в) представлена нагрузка системы пружин в контактном устройстве (контактор, реле). В точке δ н якорь находится на ограничительном упоре, к которому он прижат возвратной (отключающей) пружиной. В пределах так называемого свободного хода (по пути от упора до соприкосновения с контактными пружинами в точке δ 1) действуют вес подвижной системы, силы трения и сила возвратной пружины. При движении якоря Р мех возрастает за счет сжатия возвратной пружины. В точке δ 1 происходит соприкосновение контактов, при этом Р мех возрастает сначала скачкообразно за счет начального нажатия, а затем плавно за счет совместного противодействия возвратной и контактных пружин.
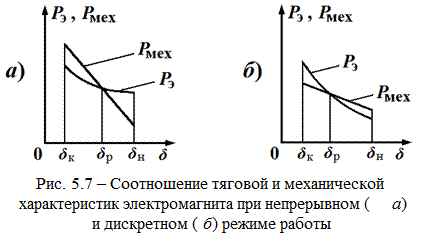
Для нормальной работы ЭМ требуется согласование его тяговой и механической характеристик, позволяющие получить непрерывный или дискретный режим работы ЭМ.
При непрерывном режиме каждому значению тока соответствует определенное значение перемещения якоря. Рабочая точка – это точка пересечения характеристик. Для получения непрерывного режима необходимо, чтобы крутизна механической характеристики была выше, чем тяговой (рис. 5.7, а). Тогда при увеличении тока точка пересечения тяговой и механической характеристик смещается влево тем больше, чем больше ток. Можно и так рассуждать: сила тяги стремится уменьшить δ, сила сопротивления – увеличить. Точка равновесия (когда якорь неподвижен) достигается при Р мех = Р э. При уменьшении δ относительно точки равновесия равнодействующая сила Р мех – Р э стремится увеличить δ, т.е. вернуть якорь в точку равновесия. При дискретном (релейном) режиме крутизна тяговой характеристики выше, чем механической (рис. 5.7, б). При отклонении от точки равновесия равнодействующая сила стремится увеличить это отклонение, т.е. равновесие является неустойчивым. Поэтому якорь может занимать только одно из двух крайних положений, которые определяются упорами: начальное и конечное. В данном режиме тяговая характеристика при срабатывании должна лежать целиком выше механической, а при отпускании — целиком ниже механической (рис. 5.8).
Отношение МДС отпускания, при котором происходит возврат якоря в исходное положение, к МДС срабатывания называется коэффициентом возврата ЭМ:
Для нейтральных ЭМ коэффициент возврата всегда меньше единицы и в зависимости от исполнения изменяется от 0,1 до 0,9; чаще всего 0,4–0,8. Рабочее значение тока выбирается с запасом: I раб = k з I сраб. Величина k з называется коэффициентом запаса. Обычно k з = 1,5–2.
Переходные процессы в электромагнитах. Анализ переходных процессов важен для определения быстродействия ЭМ. При анализе обмотку ЭМ представляют в виде последовательного соединения L и R. Индуктивность обмотки зависит от положения якоря, т.е. от величины δ. Включение ЭМ. В исходном положении якоря индуктивность обмотки имеет минимальное значение L min, а в притянутом – максимальное L max. При подаче питания в обмотку ЭМ и неподвижном якоре переходный процесс описывается уравнением
До тех пор, пока якорь не начал движение, индуктивность обмотки остается постоянной, поэтому ток в обмотке будет изменяться по экспоненте:
где I у = U / R. – установившееся значение тока в обмотке; τ min = L min/ R – минимальное значение постоянной времени обмотки. При достижении током I значения, равного току трогания I тр1, якорь начнет перемещаться. Время трогания t тр1 – это время от момента подачи питания в обмотку до момента начала перемещения якоря. Время трогания находим из (5.9):
Если под I тр1 понимать ток срабатывания, а под I у – рабочий ток I раб, то выражение (5.10) примет вид:
При движении якоря переходный процесс описывается уравнением
Время от момента начала движения якоря до момента прихода его в притянутое положение называется временем движения при срабатывании t дв1. Для электромагнитных реле обычно t дв1 < t тр1. Время от момента подачи питания в обмотку до момента полного притяжения якоря называется временем срабатывания: t сраб = t тр1 + t дв1. После остановки якоря переходный процесс описывается уравнением
где L max – индуктивность в притянутом положении якоря. Уравнение (5.13) решается с учетом ненулевых начальных условий: при t = t сраб i = I min. Без учета насыщения магнитопровода при изменении тока индуктивность можно считать постоянной, поэтому решение уравнения (5.12) имеет следующий вид:
где T max = L max/ R – постоянная времени обмотки при притянутом якоре. После окончания переходного процесса ток достигает установившегося значения I у. Выключение ЭМ. Простейший способ – разрыв цепи с помощью контакта. При разрыве цепи происходит резкое падение тока, в результате чего появляется ЭДС самоиндукции. Запасенная энергия магнитного поля переходит в электрическую энергию, которая расходуется на дуговой или искровой разряд и тепловые потери в обмотке. Следует отметить, что ЭДС самоиндукции может во много раз превышать напряжение питания. Большая ЭДС представляет опасность для обслуживающего персонала и может вызвать повреждение обмотки. Наличие дуги или искры позволяет переходный процесс при отключении обмотки описывать с помощью уравнения, аналогичного (5.13):
где R д– сопротивление дуги (или искры). Обычно сопротивление дуги изменяется в функции времени. Однако для упрощения часто предполагают R д = const [но это грубо]. Тогда решение представляет собой экспоненту с довольно малой постоянной времени, так как обычно R д >> R. См. рис. 5.10 [ изобразить примерно на доске].
Когда ток уменьшится до значения, при котором электромагнитная сила становится меньше механической (силы возвратной пружины), начнется перемещение якоря в исходное положение. Время от момента отключения обмотки до момента начала движения якоря называется временем трогания при отпускании t тр2. При движении якоря происходит уменьшение индуктивности, вследствие чего изменяется характер переходного процесса и в кривой тока появляется всплеск. Время от момента начала движения якоря до момента его прихода в исходное положение называется временем движения при отпускании t дв2. После остановки якоря ток будет снова уменьшаться, пока дуга не погаснет. Временем отпускания называется время от момента отключения обмотки до момента прихода якоря в исходное положение: t отп = t тр2 + t дв2. Для уменьшения ЭДС самоиндукции в некоторых случаях параллельно обмотке подключается т.н. разрядный резистор R р(см. рис. 5.11). В этом случае при отключении обмотки переходный процесс описывается уравнением
Решая это уравнение с учетом ненулевого начального условия i (0) = I у, получаем
Отсюда получаем выражение для времени трогания:
Из (5.16) легко получить также выражение для ЭДС самоиндукции
Максимальное напряжение на обмотке ЭМ возникает при t = 0 и равно I у R р = UR р/ R. Таким образом, при уменьшении R р уменьшается перенапряжение, зато увеличивается время отключения и увеличивается расход электроэнергии при включенном ЭМ. Процессы срабатывания и отпускания ЭМ рассматривались без учета влияния вихревых токов, создаваемых в магнитопроводе при изменении магнитного потока во время переходных процессов. При срабатывании ЭМ вихревые токи в соответствии с принципом Ленца препятствуют возрастанию магнитного потока обмотки, что приводит к увеличению времени срабатывания. При отпускании ЭМ вихревые токи препятствуют уменьшению магнитного потока обмотки, что также приводит к увеличению времени отпускания. В зависимости от значений t сраб и t отп ЭМ делятся на быстродействующие t сраб и t отп менее 0,05 с), нормальные (t сраб и t отп лежат в интервале от 0,05 до 0,15 с) и замедленного действия (t сраб и t отп более 0,15 с). Способы изменения временных параметров ЭМ. Для изменения временных параметров ЭМ применяют конструктивные и схемные способы. Конструктивные способы. Для уменьшения времени срабатывания и отпускания ЭМ стремятся ослабить влияние вихревых токов. Этого достигают, выполняя магнитопровод из материала с большим удельным электрическим сопротивлением (кремнистые стали, низконикелевые пермаллои). Магнитопровод собирают из шихтованной электротехнической стали. Для уменьшения времени движения уменьшают ход якоря и его массу. Для уменьшения времени отпускания увеличивают высоту штифта отлипания, которая оказывает большое влияние на время отпускания, почти не изменяя время срабатывания. Для замедления процессов срабатывания и отпускания широко применяется электромагнитное демпфирование, при котором используется короткозамкнутая обмотка. Короткозамкнутая обмотка обычно представляет собой сплошную медную втулку, размещенную на сердечнике магнитопровода. Во время срабатывания ЭМ поток обмотки наводит во втулке ЭДС взаимоиндукции, ток которой создает магнитный поток,, направленный встречно по отношению к потоку обмотки. В результате взаимодействия потоков в ЭМ образуется результирующий магнитный поток Ф, изменение которого происходит замедленно. Наиболее эффективно короткозамкнутая втулка действует при отпускании, так как в притянутом положении якоря индуктивность ЭМ значительно больше, чем в исходном положении. Поэтому время выдержки при отпускании может быть получено в 8–12 раз большим, чем при срабатывании и может превышать 1 с. При отключении ЭМ с короткозамкнутой втулкой перенапряжение на обмотке значительно меньше, так как оно пропорционально dΨ / dt, а скорость спада потокосцепления значительно снижена. Можно представить и так: энергия магнитного поля расходуется не на создание дуги, а на создание тока в короткозамкнутой втулке. Для получения больших выдержек времени (до нескольких секунд) применяют механические способы замедления движения якоря с помощью часового механизма, пневматических или гидравлических демпфирующих устройств. Для увеличения силы противодействия, создаваемой механическими устройствами, их присоединяют к якорю через повышающую зубчатую передачу. Схемные способы. Как видно из выражений (5.9) и (5.16), время трогания зависит от постоянной времени и установившегося значения тока.
На рис. 5.11 показаны различные схемы, с помощью которых можно изменять временные параметры ЭМ. Схема, приведенная на рис. 5.11, а, позволяет уменьшить время срабатывания за счет повышения напряжения U и подключения дополнительного резистора R доп. Уменьшение времени трогания обеспечивается уменьшением постоянной времени, а установившийся ток остается прежним. Увеличение быстродействия сопряжено с ростом потерь на резисторе R доп. Дальнейшего уменьшения времени трогания в рассматриваемой схеме можно добиться подключением конденсатора С параллельно резистору R доп.Подключение конденсатора С приводит к форсировке тока, так как при подаче питания в первый момент времени напряжение на конденсаторе равно нулю и он закорачивает резистор R доп, подключая повышенное напряжение питания непосредственно к обмотке. Емкость конденсатора выбирается с учетом условия апериодического характера переходного процесса. На рис. 5.11, б показана схема форсировки тока, позволяющая уменьшить время срабатывания. Размыкание контакта S происходит в притянутом положении якоря. При подаче питания дополнительный резистор шунтируется контактом S, и напряжение U непосредственно подключено к обмотке. После срабатывания ЭМ контакт S размыкается, и напряжение U подключается к обмотке через резистор R доп. При этом можно получить заметную экономию затрачиваемой мощности, так как ток отпускания значительно меньше тока срабатывания. На рис. 5.11, в показана схема, позволяющая увеличить время срабатывания за счет включения дополнительной индуктивности, при этомпостоянная времени ЭМ увеличивается, а ток управления не меняется. На рис. 5.11, г — е показаны схемы, позволяющие увеличить время отпускания. Параллельное подключение шунтирующего резистора к обмотке (рис. 9.15, г) приводит к созданию замкнутого контура при отключении и замедлению протекания электромагнитных процессов. В схеме, приведенной на рис. 5.11, д,уменьшение потерь достигается последовательным подключением к резистору R ш конденсатора С. В схеме, представленной на рис. 5.11, е, вместо резистора R ш включен полупроводниковый диод в обратном направлении по отношению к напряжению источника питания. В установившемся режиме потери в диоде отсутствуют. При отключении в обмотке возникает ЭДС самоиндукции, отпирающая диод. При этом обмотка замыкается диодом почти накоротко.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.247.76 (0.065 с.) |
 Действие нейтрального ЭМ не зависит от направления тока в обмотке электромагнита. При отсутствии тока магнитный поток практически равен нулю. В зависимости от принципа действия и назначения нейтральные ЭМ имеют различное конструктивное исполнение. Вместе с тем каждый ЭМ содержит (рис. 5.1) обмотки 1 и магнитопровод. Магнитопровод выполнен из ферромагнитного материала и состоит из неподвижной части (сердечник 2 и ярмо 3) и подвижной части (якоря) 4. В некоторых ЭМ имеется несколько обмоток.
Действие нейтрального ЭМ не зависит от направления тока в обмотке электромагнита. При отсутствии тока магнитный поток практически равен нулю. В зависимости от принципа действия и назначения нейтральные ЭМ имеют различное конструктивное исполнение. Вместе с тем каждый ЭМ содержит (рис. 5.1) обмотки 1 и магнитопровод. Магнитопровод выполнен из ферромагнитного материала и состоит из неподвижной части (сердечник 2 и ярмо 3) и подвижной части (якоря) 4. В некоторых ЭМ имеется несколько обмоток.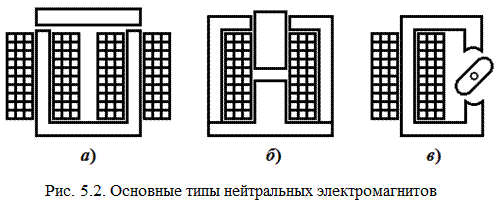
 (5.1)
(5.1)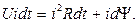 (5.2)
(5.2)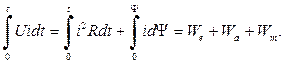 (5.3)
(5.3)
 Отсюда можно получить простые выражения для энергии магнитного поля W м, преобразованной в механическую энергию: она пропорциональна площади фигуры 0 am 0. Нетрудно найти чисто геометрически: до начала трогания запасена энергия магнитного поля W м1 = I Y1/2; в процессе движения запасена энергия W м1 = I (Y2 – Y1); в механическую энергию превратилась часть
Отсюда можно получить простые выражения для энергии магнитного поля W м, преобразованной в механическую энергию: она пропорциональна площади фигуры 0 am 0. Нетрудно найти чисто геометрически: до начала трогания запасена энергия магнитного поля W м1 = I Y1/2; в процессе движения запасена энергия W м1 = I (Y2 – Y1); в механическую энергию превратилась часть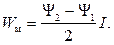 (5.4)
(5.4)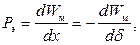 (5.5)
(5.5)
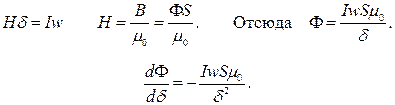 (5.6)
(5.6)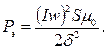 (5.7)
(5.7)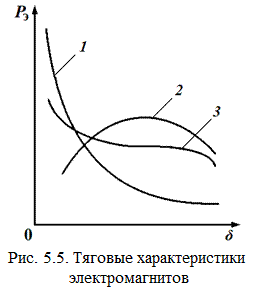 Полученная зависимость (5.7) показана на рис. 5.5 (кривая 1). Как видно, тяговая характеристика ЭМ в случае плоскопараллельных полюсов имеет крутой спад.
Полученная зависимость (5.7) показана на рис. 5.5 (кривая 1). Как видно, тяговая характеристика ЭМ в случае плоскопараллельных полюсов имеет крутой спад.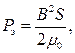 (5.8)
(5.8)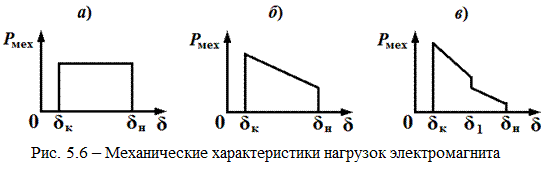
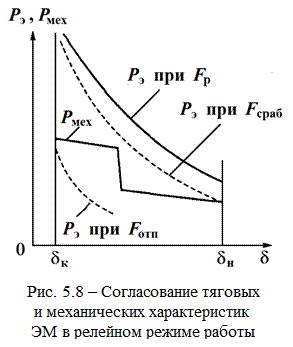 Минимальное значение МДС (тока), при котором электромагнитная сила в точке δ = δ нпревышает механическую и происходит срабатывание ЭМ (перемещение якоря от δ н до δ к), называется МДС (током) срабатывания F сра6(I сра6). Максимальное значение МДС (тока), при котором электромагнитная сила в точке δ = δ кне может удержать якорь в притянутом положении, вследствие чего якорь возвращается в исходное положение, называется МДС (током) отпускания F отп(I отп). Тяговые характеристики ЭМ при F сра6 и F отпне должны пересекаться с механической характеристикой в области зазоров δ к < δ < δ н .При неправильном согласовании характеристик якорь может остановиться в промежуточном положении.
Минимальное значение МДС (тока), при котором электромагнитная сила в точке δ = δ нпревышает механическую и происходит срабатывание ЭМ (перемещение якоря от δ н до δ к), называется МДС (током) срабатывания F сра6(I сра6). Максимальное значение МДС (тока), при котором электромагнитная сила в точке δ = δ кне может удержать якорь в притянутом положении, вследствие чего якорь возвращается в исходное положение, называется МДС (током) отпускания F отп(I отп). Тяговые характеристики ЭМ при F сра6 и F отпне должны пересекаться с механической характеристикой в области зазоров δ к < δ < δ н .При неправильном согласовании характеристик якорь может остановиться в промежуточном положении.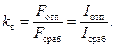
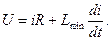
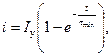 (5.9)
(5.9)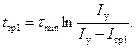 (5.10)
(5.10) (5.11)
(5.11)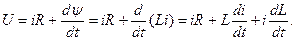 (5.12)
(5.12)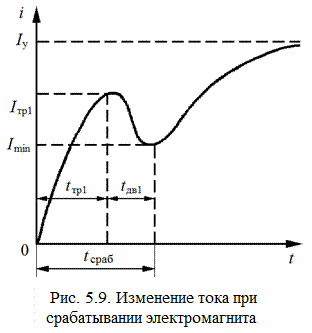 Третье слагаемое в правой части уравнения (5.12) обусловлено изменением индуктивности во время движения якоря. Перемещение якоря при его срабатывании приводит к росту индуктивности, следовательно, это слагаемое будет больше нуля. Поэтому по сравнению с неподвижным якорем к обмотке как бы прикладывается меньшее напряжение, что приводит к некоторому уменьшению тока (рис. 5.9). Для определения характера изменения тока необходимо решить уравнение (5.12) совместно с уравнением движения якоря, что в общем случае весьма затруднительно.
Третье слагаемое в правой части уравнения (5.12) обусловлено изменением индуктивности во время движения якоря. Перемещение якоря при его срабатывании приводит к росту индуктивности, следовательно, это слагаемое будет больше нуля. Поэтому по сравнению с неподвижным якорем к обмотке как бы прикладывается меньшее напряжение, что приводит к некоторому уменьшению тока (рис. 5.9). Для определения характера изменения тока необходимо решить уравнение (5.12) совместно с уравнением движения якоря, что в общем случае весьма затруднительно.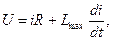 (5.13)
(5.13)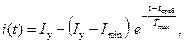
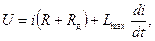 (5.14)
(5.14)
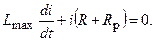 (5.15)
(5.15) (5.16)
(5.16)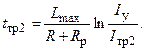 (5.17)
(5.17) (5.18)
(5.18)