Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к выполнению работыСтр 1 из 7Следующая ⇒
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
С.А.Суслова Н.П. Гвозденко РЕШЕНИЕ ЗАДАЧ В MS EXCEL Учебное пособие
Липецк Липецкий государственный технический университет 2017 УДК004.4(07) С904 Рецензенты:
кафедра гуманитарных и естественнонаучных дисциплин МОУ ВО ″Институт права и экономики» г. Липецк (зав. каф., доц. А.А. Прибыткова); В.В. Кургасов, канд. пед. наук, доц. кафедрыестественно-научных и технических дисциплин ЛКИТиУ филиала ФГБОУ ВО «МГУТиУ имени К.Г.Разумовского(ПКУ)».
Суслова, С.А. С904Решение задач в MS EXCEL [Текст]: учеб. пособие / С.А. Суслова, Н.П. Гвозденко, – Липецк: Изд-во Липецкого государственного технического университета, 2017. – 85 с.
ISBN978-5-88247-847-5 Учебно-методическое пособие представляет собой практическое руководство по освоению способов работы, инструментов и методов решения типовых математических задач с помощью табличного процессора Мiсrоsоft Excel. Приводятся варианты выполнения лабораторных работ по дисциплине «Информатика». Пособие предназначено для студентов технических специальностей очной и очно-заочной форм обучения.
Табл. 37. Ил.45. ISBN978-5-88247-847-5 Ó ФГБОУ ВО «Липецкий государственный технический университет»,2017
Содержание
Введение. 5 Лабораторная работа № 1 Табулирование функции. 6 Лабораторная работа № 2 Вычисление экстремума функции. 8 Лабораторная работа № 3 Построение графика функции одной переменной. 9 Лабораторная работа № 4 Вычисление производных в точке. 10 Лабораторная работа № 5 Построение графика функции, заданной параметрически. 12 Лабораторная работа № 6 Построение графика функции, заданной вполярной системе координат. 13 Лабораторная работа № 7 Построение графика объемной функции. 15 Лабораторная работа № 8 Численное решение дифференциального уравнения первого порядка. 16 Лабораторная работа № 9 Численное решение дифференциального уравнения второго порядка. 19 Лабораторная работа № 10
Решение системы нелинейных уравнений. 24 Лабораторная работа № 11 Приближенное вычисление определенных интегралов. 26 Лабораторная работа № 12 Нахождение корней нелинейного уравнения. 29 Лабораторная работа № 13 Решение системы линейных уравнений. 31 Лабораторная работа № 14 Решение задачи линейной оптимизации (производственный план) 33 Лабораторная работа № 15 Парная регрессия. 37 Лабораторная работа № 16 Множественная регрессия. 47 Библиографический список. 50 ПРИЛОЖЕНИЕ. 51 Варианты заданий для лабораторных работ № 1, 2, 3. 51 Варианты заданий для лабораторной работы № 4. 52 Варианты заданий для лабораторной работы № 5. 54 Варианты заданий для лабораторной работы № 6. 58 Варианты заданий для лабораторной работы № 7. 61 Варианты заданий для лабораторной работы № 8. 62 Варианты заданий для лабораторной работы № 9. 64 Варианты заданий для лабораторной работы №10. 65 Варианты заданий для лабораторной работы № 11. 66 Варианты заданий для лабораторной работы № 12. 68 Варианты заданий для лабораторной работы №13. 69 Варианты заданий для лабораторной работы № 14. 69 Варианты заданий к лабораторной работе № 15 82 Варианты заданий к лабораторной работе № 16. 83 Исходные данные для выполнения расчётов аппроксимации. 84
Введение
Весьма важным в подготовке студентов является изучение офисных программных продуктов, к которым относится семейство электронных таблиц. Табличный процессор - это некая прикладная программа, предназначенная для проведения табличных расчетов и сложных вычислений по формулам. Издавна многие расчеты выполняются в табличной форме, особенно в области делопроизводства: многочисленные расчётные ведомости, табуляграммы, сметы расходов и тому подобное. Помимо этого, решение численными методами целого ряда математических задач удобно выполнять именно в табличной форме. Табличный процессор MS Excel (электронные таблицы) - одно из наиболее часто используемых приложений пакета MSOffice, мощнейший инструмент, значительно упрощающий рутинную повседневную работу. Его основное назначение - решение практически любых задач расчётного характера, входные данные которых можно представить в виде таблиц.
Он предоставляет возможности математических, статистических и экономических расчётов, ряд графических инструментов и функционал макропрограммирования на основе языка VBA (Visual Basic for Applications). Excel на сегодняшний день является одним из наиболее популярных табличных процессоров в мире. В данном учебном пособии на различных примерах продемонстрированы широкие возможности MS Excel. Описываются способы работы, инструменты и методы решения типовых математических задач, задач прикладного характера, которые связаны с решением линейных и нелинейных уравнений, систем линейных уравнений и построением различного рода графиков и поверхностей. Приводятся указания к выполнению лабораторных работ, позволяющих приобрести практические навыки работы с приложением. Пособие содержит варианты задач для самостоятельной работы. Лабораторная работа №1 Табулирование функции Задание Составить таблицу значений аргумента x и функции
Лабораторная работа № 2 Задание По данным примера из лабораторной работы №1 найти минимум функции Лабораторная работа № 3 Задание Построить график функции: Лабораторная работа № 4 Задание Найти три производные функциинормального распределения
Лабораторная работа № 5 Задание Построить график кривой, называемой ''Лемниската Бернулли'': Лабораторная работа № 6 Полярной системе координат Задание Построить график кривой, называемой '' n -лепестковой розой'':
Лабораторная работа №7 Задание Построить график объёмной функции
Лабораторная работа № 8 Задание Найти решение дифференциального уравнения Составить таблицу значений аргумента Лабораторная работа № 9 Задание Найти решение дифференциального уравнения Составить таблицу значений аргумента Лабораторная работа № 10 Задание Решить систему нелинейных уравнений
Лабораторная работа № 11 Задание Вычислить интеграл
Метод прямоугольников Разбиение интервала интегрирования
Суммирование значений таких площадей
Метод трапеций Замена интеграла
на каждом элементарном участке площадью трапеции с основаниями
Метод Симпсона (парабол) Разбиение промежутка Площадь фигуры, ограниченной сверху параболой, считается по формуле
Суммирование таких интегралов (площадей, ограниченных параболами) приводит к более точной, чем предыдущие, формуле
Решение 1. Оформите лист Excel следующим образом (рис. 21):
Рис. 21. Шапка таблицы 2. Введите формулы: в ячейку С4: = (B4– в ячейку В6: =А4; в ячейку С6: =КОРЕНЬ(2*В6+1), определяющие значение подынтегральной функции. 3. Введите формулу в ячейку B7: =В6+$C$4. Затем заполните столбец В с помощью маркера автозаполнения. 4. Затем выделите ячейку С6, и проделайте то же самое в столбце С.
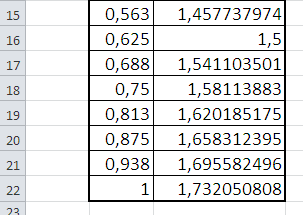
Рис. 22. Результаты вычисления интеграла различными способами
5. В ячейки E5, F5 и G5 введите следующие формулы: E5: = C4*CУММ (С6:С22); F5: = C4*((C6+C22)/2+CУММ (С6:С21); G5: = C4/3*((C6+4*(C7+C9+C11+C13+C15+C17+C19+C21)+ 2*(С8+c10+c12+c14+c16+c18+c20)+c22). Результаты вычисления интеграла представлены на рис. 22.
Лабораторная работа №12 Задание Определить все корни уравнения
при a = 1; b = – 5,5; c = – 50; p = 112,5. Лабораторная работа № 13 Задание Решить систему линейных алгебраических уравнений вида
где А – матрица коэффициентов размера 3 × 3, А; В – вектор-столбец правых частей размера 3 × 1, В. Лабораторная работа № 14 Решение задачи линейной оптимизации (производственный план) Задание На металлургическом предприятии используется три типа оборудования (травильный агрегат, прокатный стан и печи отжига) для выпуска проката трёх видов: А, В и С. Загрузка указанного оборудования на 1 т проката каждого вида, общее время работы оборудования, объём выпуска и стоимость проката (в условных единицах) каждого вида приведены в табл.1.
Таблица 1 Тип оборудования |
Фонд полезного Времени работы (час/месяц)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| А | В | С | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Травильный агрегат | 0,083 | 0,083 | 0,104 | 624 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прокатный стан | 0,067 | 0,100 | 0,083 | 416 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Печи отжига | 3,500 | 2,800 | 0,000 | 2766 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Стоимость 1 т проката | 35,00 | 25,00 | 40,00 | - | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Выпуск, не более, (т) | 250,00 | 1250,00 | 1500,00 | - | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Требуется определить программу выпуска проката, при которой ежемесячный общий выпуск проката в денежном выражении был бы максимальным.
Лабораторная работа № 15
Парная регрессия
Задание
На основании данных для соответствующего варианта:
1. Построить предложенные уравнения регрессии, включая линейную регрессию.
2. Вычислить индексы парной корреляции для каждого уравнения.
3. Проверить значимость уравнений регрессии и отдельных коэффициентов линейного уравнения.
4. Определить лучшее уравнение регрессии на основе средней ошибки аппроксимации.
Пример выполнения работы
Построить уравнение регрессии между выходной толщиной h 1 и входной толщиной h 0 холоднокатаной полосы. Значения толщин x = h 0 и y = h 1 даны в таблице 2.
Регрессионный анализ в Excel невероятно прост. Как только данные представлены в графическом виде, регрессия выполняется с помощью нескольких щелчков мыши, поэтому регрессия с использованием прямой часто применяется, несмотря на то, что зависимость между переменными не линейная, а более сложная.
Сформулируем практическое правило: всегда следует строить диаграмму, на которой представлена кривая регрессии и данные, чтобы можно было визуально оценить степень совпадения. В том случае, когда регрессия проводится с помощью линии тренда, кривая регрессии автоматически добавляется на диаграмму с соответствующими данными.
Таблица 2
| xi ·10-2 | 71 | 78 | 84 | 92 | 87 | 85 | 86 | 91 | 93 | 93 | 90 | 85 | 81 | 80 | 78 | 84 | 82 | 85 | 82 | 80 |
| yi ·10-2 | 46 | 50 | 54 | 54 | 52 | 50 | 49 | 53 | 57 | 59 | 56 | 53 | 50 | 48 | 50 | 54 | 55 | 55 | 54 | 54 |
1. Подготовьте начальный рабочий лист с исходными данными (рис. 32), постройте точечную диаграмму.
2. При построении на диаграмме линии тренда Excel автоматически находит значения коэффициентов a и b, а также квадрат коэффициента корреляции (достоверность аппроксимации) R2.
3. Уравнение линии тренда и значение R2 по умолчанию на диаграмме не отображаются. Чтобы отобразить эту информацию, следует в нижней части диалога Параметры линии тренда поставить флажки в параметрах:
þ показывать уравнение на диаграмме;
þ поместить на диаграмме величину достоверности аппроксимации (R2).
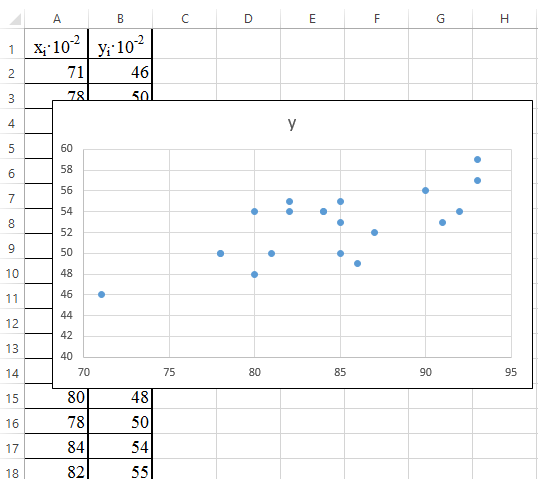
Рис. 32. Исходные данные и точечная диаграмма
4. Щелкните правой кнопкой мыши на любом из маркеров данных и вконтекстном меню выберите команду Добавить линию тренда... (рис. 33).
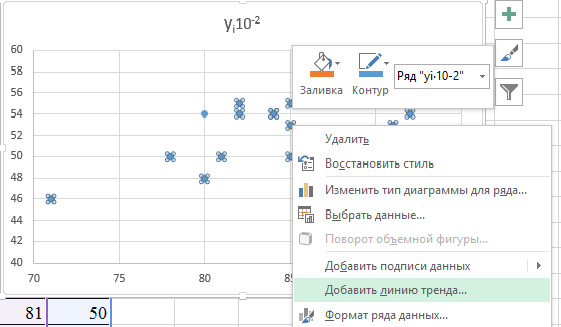
Рис. 33. Контекстное меню
5. В диалоговом окне Параметры линии тренда выберите тип диаграммы Линейная (рис. 34).
6. Отобразите уравнение кривой регрессии на диаграмме, и величину достоверности аппроксимации (R 2).
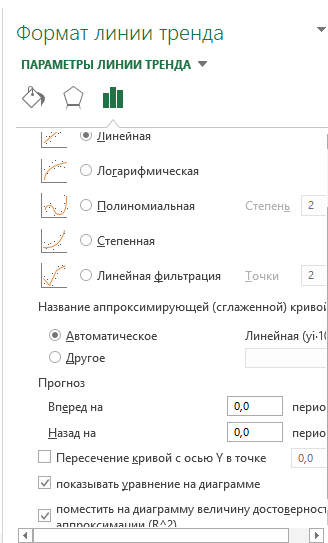
Рис. 34. Параметры линии тренда
7. Как видно из диаграммы (рис. 35), уравнение регрессии имеет вид
y = 0,4108· х + 18 с достоверностью аппроксимации R 2 = 0,5223.
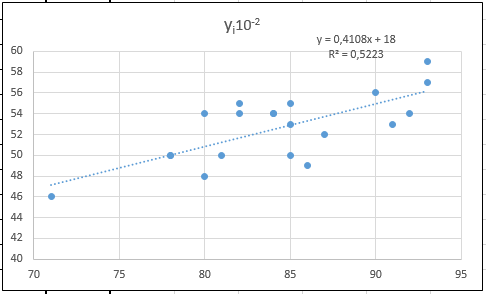
Рис. 35. Линейная модель
8. Рассчитаем среднюю ошибку аппроксимации, предварительно сформировав в столбце С массив значений 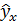 . Для этого введите следующие формулы:
. Для этого введите следующие формулы:
|
|
в ячейку С2: = 0,4108*А2 + 18;
в ячейку D2: =ABS((B2 – D2)/B2 (рис. 36).
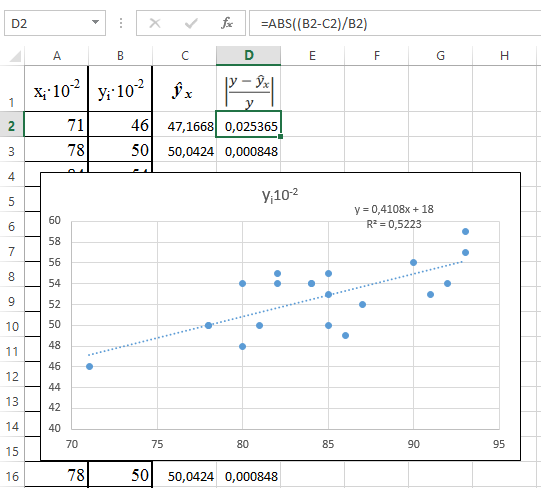
Рис. 36. Расчёт модельных значений и относительной ошибки
9. В ячейку D25 введите формулу: =1/20*D22*100 (рис. 37).
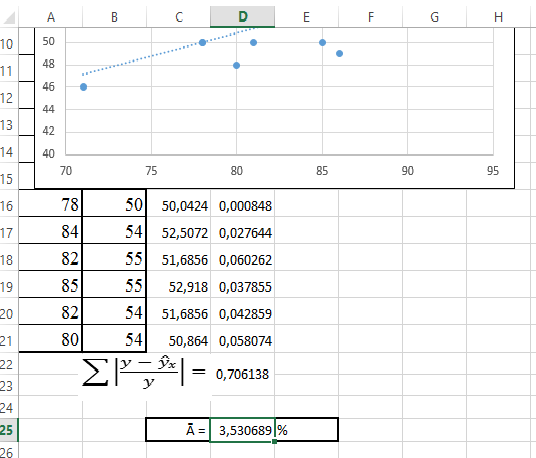
Получаем: R 2 = 0,5223, 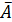 = 3,53%. Построенное уравнение регрессии считается удовлетворительным, поскольку значение
= 3,53%. Построенное уравнение регрессии считается удовлетворительным, поскольку значение 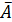 не превышает 10-12%.
не превышает 10-12%.
Рис. 37. Расчёт средней ошибки аппроксимации для линейной модели
10. Рассчитайте F факт и F табл. Для этого в ячейки D27 и D28 введитеследующие формулы:
D27: = КОРРЕЛ(A2:A21;B2:D21)^2/(1 -КОРРЕЛ(A2:A21;B2:D21)^2)*18;
D28: = FРАСПОБР(0,05;1;18). Получаем F факт=19,6809, F табл=4,413873.
Так как F ma6л< F факт, то H 0 - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность (рис. 37).
Поскольку идеальной аппроксимации соответствует величина R 2 = 1, можно сделать вывод, что прямая линия не описывает зависимости идеально. Нужно попытаться подобрать другую кривую регрессии, обладающую некоторой кривизной.
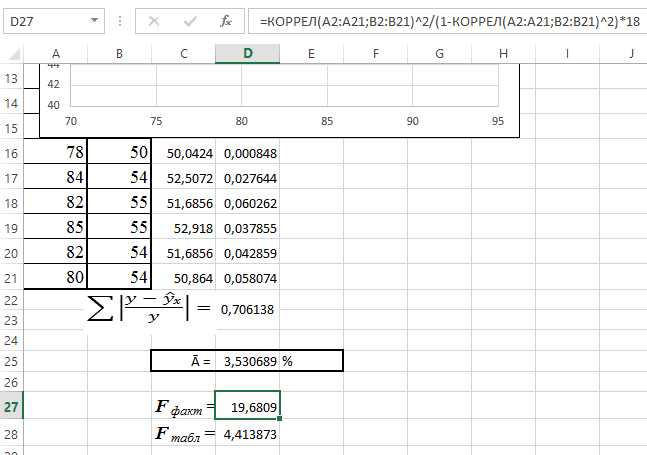
Рис. 38. Расчёт фактического и табличного значения F-критерия Фишера
11. Рассчитаем параметры полиномиальной и экспоненциальной модели. Результаты моделирования и расчётов приведены на рис. 39 и 40.
12. В ячейку G2 введите формулу: = - 0,0036*А2^2 + 1,0193*A2 - 7,3346.
Видно, что лучше всего экспериментальные данные описывает линейная зависимость, т.к. у линейной регрессии величина 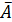 минимальна.
минимальна.
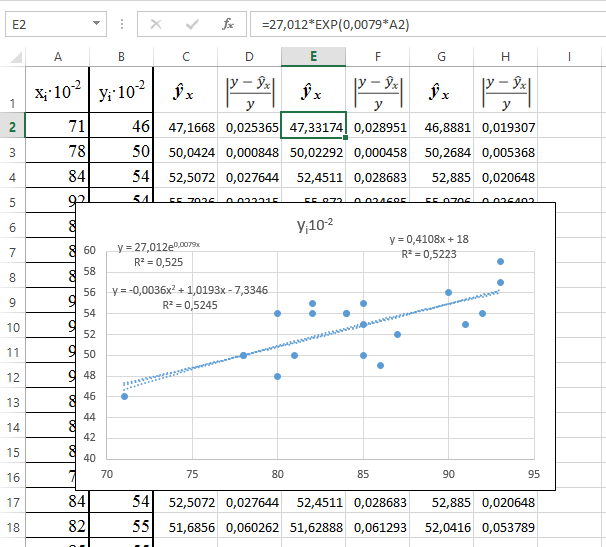
Рис. 39. Параметры экспоненциальной аппроксимации
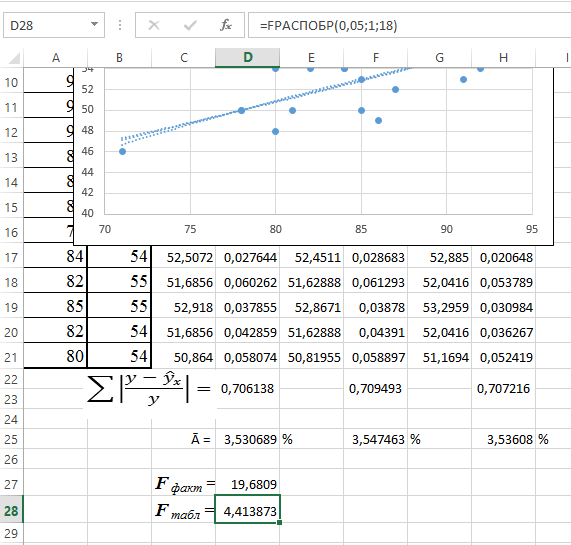
Рис. 40. Параметры параболической аппроксимации
Лабораторная работа № 16
Множественная регрессия
Задание
На основании данных для соответствующего варианта:
1. Отобрать значимые аргументы для построения уравнения регрессии.
2. Построить уравнение линейной регрессии.
3. Определить коэффициент множественной корреляции.
4. Проверить значимость уравнения при уровнях значимости 0,05 и 0,01.
Таблица А
Регрессионная статистика
Рис. 43. Регрессионная статистика
| Дисперсионный анализ |
Таблица Б | |||||||||||
| df | SS | MS | F | Значимость F | ||||||||
| Регрессия | 2 | 2 326,14 | 163,07 | 19,27 | 7,35154E-06 | |||||||
| Остаток | 26 | 1 569,04 | 60,35 | |||||||||
| Итого | 28 | 3 895,17 |
|
|
| |||||||
| Рис. 44. Дисперсионный анализ | ||||||||||||
|
Таблица В | ||||||||||||
| Коэффи-циенты | Стандарт ная ошибка | t- статистика | P- Значение | Нижние 95% | Верхние 95% | |||||||
| у-пересечение | 92,585 | 8,35 | 11,09 | 2,3E-11 | 75,42 | 109,75 | ||||||
| х2 | 1,761 | 0,55 | 3,22 | 0,0034 | 0,64 | 2,89 | ||||||
| хЗ | 0,397 | 0,13 | 2,95 | 0,0066 | 0,12 | 0,67 | ||||||
Рис. 45. Коэффициенты уравнения
6. Из таблицы В следует, что уравнение регрессии имеет вид
ŷ = 92,585 + 1,761· х2 + 0,397· х3.
7. Коэффициент множественной корреляции определяется из таблицы А:

8. Проверка значимости уравнения регрессии основана на использовании F -критерия Фишера. Фактическое значение критерия берётся из таблицы Б, то есть F факт =19,27.
9. Для определения табличных значений используйте встроенную функцию {=FРАСПОБР(α; k 1; k 2)}.
10. Задайте параметры k 1 = 2; k 2 = 29-2 -1= 26; α = 0,05 и α = 0,01. Получите F факт.0,05 = 3,369, F факт.0,01 = 5,526. Откуда следует, что уравнение регрессии значимо и при α = 0,05 и при α = 0,01.
Библиографический список
1. Шанченко, Н. И. Эконометрика: лабораторный практикум [Текст]:учеб.-метод. пособие/ Н. И. Шанченко – Ульяновск: УлГТУ, 2004. – 79 с.
2. Гарнаев, А.Ю. Использование MS Excel, VBA в экономике и финансах[Текст]: / А.Ю. Гарнаев.– СПб.: БХВ – Петербург, 1999.– 336 с.
3. Гвозденко, Н.П. Программирование на VBA [Текст]: методические указания к лабораторно-практическим занятиям на ПЭВМ (для технических специальностей) / Н.П. Гвозденко, С.А. Суслова. Липецк: ЛГТУ, 2005. – 36 с.
4. Гвозденко, Н.П. Программирование на VBA [Текст]: Сборник заданий к лабораторно-практическим занятиям на ПЭВМ (для технических специальностей) / Н.П. Гвозденко, С.А. Суслова. – Липецк: ЛГТУ, 2007. – 64 с.
ПРИЛОЖЕНИЕ
Таблица 1
Варианты заданий к лабораторным работам №1, 2,3
| № вар. | Функция Y |
Параметры | Границы интервала [ | Шаг | |||
| a | b | c | 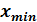
| 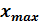
| |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 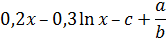
| 4 | 2 | 0,6 | 1 | 20 | 1,5 |
| 2 | 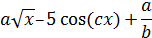
| 4 | 2 | 1,2 | 0,6 | 2 | 0,10 |
| 3 | 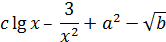
| 0,43 | 9 | 6 | 0,1 | 3 | 0,32 |
| 4 | 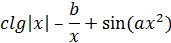
| 0,2 | 6 | 8 | -2 | 3 | 0,51 |
| 5 | 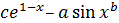
| 8 | 2 | 4 | -1 | 1,5 | 0,10 |
| 6 | 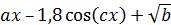
| 1,2 | 12 | 0,58 | 0,2 | 1,5 | 0,12 |
| 7 | 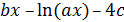
| 0,3 | 2 | 4 | 0,1 | 2 | 0,32 |
| 8 | 
| 1 | 2 | 0,34 | 0,1 | 2 | 0,15 |
| 9 | 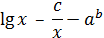
| 0,56 | 2 | 5 | 1 | 10 | 1,0 |
| 10 | 
| 1,2 | 4 | 8 | -0,5 | 3 | 0,25 |
| 11 | 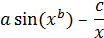
| 8 | 2 | 0,1 | -1 | 2 | 0,15 |
| 12 | 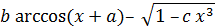
| 0,32 | 2 | 0,1 | 0,1 | 2 | 0,10 |
| 13 | 
| 1,5 | 0,64 | 2 | -1 | 1 | 0,32 |
| 14 | 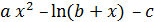
| 0,3 | 1 | 3 | 0,1 | 6 | 0,51 |
| 15 | 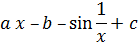
| 0,3 | 1 | 1 | 0,1 | 10 | 1,0 |
| 16 | 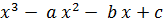
| 112,5 | 5,5 | 30 | -1 | 5 | 0,25 |
|
Окончание табл. 1 | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 17 | 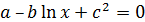
| 10 | 2 | 1,34 | 0,1 | 3 | 0,32 |
| 18 | 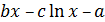
| 1,8 | 0,2 | 0,3 | 5 | 20 | 2,5 |
| 19 | 
| 12 | 5 | 6 | -1 | 3 | 1,0 |
| 20 | 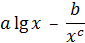
| 9,2 | 3 | 2 | 1 | 3 | 0,25 |
| 21 | 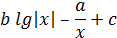
| 1 | 8 | -1 | -4 | 3 | 0,72 |
| 22 | 
| 20 | 4 | 1 | 0,01 | 1,5 | 0,15 |
| 23 | 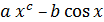
| 5 | 1,8 | 2 | -1 | 1,5 | 0,12 |
| 24 | 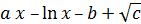
| 5 | 4 | 2 | 0,05 | 2 | 0,5 |
| 25 | 
| 5 | 2 | 1 | -1 | 2 | 0,20 |
| 26 | 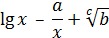
| 2 | 16 | 4 | 0,3 | 10 | 1,25 |
| 27 | 
| 15 | 10 | 4 | 0,01 | 3 | 0,15 |
| 28 | 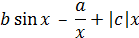
| 1 | 8 | 3,52 | 0,1 | 2 | 0,12 |
| 29 | 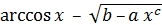
| 0,3 | 1 | 3 | 0,1 | 2 | 0,1 |
| 30 | 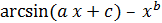
| 1,5 | 2 | 1 | -2 | 1 | 0,1 |
Таблица 2
Варианты заданий к лабораторной работе №4
| Правая часть дифференциального уравнения у ´ = f (x, y) | Интервал [ a; b ] | Число отрезков n | Начальное условие у (а) | |
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 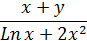
| 0,1; 1,5 | 49 | 2,1 | |
| 2 | 
| 0,1; 2 | 38 | 1,0 |
| Продолжение табл. 2 | ||||
| 1 | 2 | 3 | 4 | 5 |
| 3 | 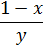
| 5; 10 | 50 | 1,0 |
| 4 | 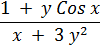
| 0; 0,5 | 50 | 2,0 |
| 5 | 
| 0; 2 | 100 | 0 |
| 6 | 
| 0; 1 | 100 | 1,0 |
| 7 | x + y | 0; 1 | 50 | 1,0 |
| 8 | x2 + y2 | 0; 1 | 100 | 0,1 |
| 9 | 
| 1; 2 | 100 | π/4 |
| 10 | 2xy + xy2 | 1; 2 | 50 | 3/2 |
| 11 | 2 x + Cosy | 1; 2 | 100 | 0 |
| 12 | 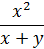
| 0; 2 | 100 | 0 |
| 13 | 
| 1; 2 | 50 | 0 |
| 14 | 
| 1; 2 | 100 | 0 |
| 15 | 
| π; 2π | 50 | 2 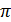
|
| 16 | 
| 0; 1 | 100 | 0 |
| 17 | 
| 0; 1 | 100 | -1 |
| 18 | 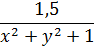
| 0; 1 | 50 | 0 |
| Окончание табл. 2 | ||||
| 1 | 2 | 3 | 4 | 5 |
| 19 | 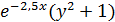
| 0; 1 | 50 | 0 |
| 20 | 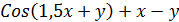
| 0; 1 | 100 | 0 |
| 21 | 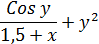
| 0; 1 | 100 | 0 |
| 22 | 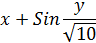
| 1,6; 4 | 120 | 2,9 |
| 23 | 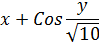
| 0,6; 4,2 | 130 | 0,8 |
| 24 | 
| 1,6; 5,2 | 78 | 4,6 |
| 25 | 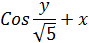
| 1,8; 4,2 | 60 | 2,6 |
| 26 | 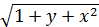
| 0,8; 5 | 55 | 3,8 |
| 27 | 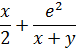
| 1,8; 4,6 | 70 | 4,5 |
| 28 | 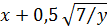
| 3; 8,6 | 70 | 6,1 |
| 29 | 
| 0,8; 4,4 | 90 | 1 |
| 30 | 
| 0,3; 3,1 | 70 | 0,2 |
Варианты заданий к лабораторной работе №5
1. Построить график кривой, называемой «циклоидой»:
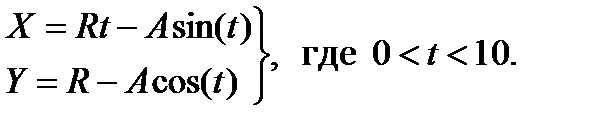
2. Построить график кривой, называемой «трохоидой»:
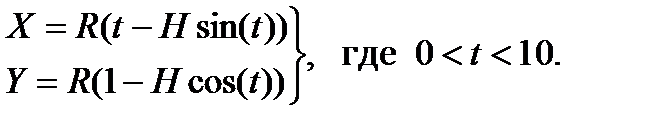
3. Построить график кривой, называемой «астроидой»:

4. Построить график кривой, называемой «гипоциклоидой»:
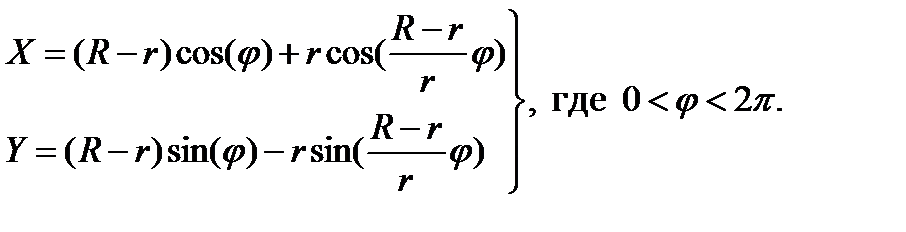
5. Построить график кривой, называемой «гиперболической спиралью»:
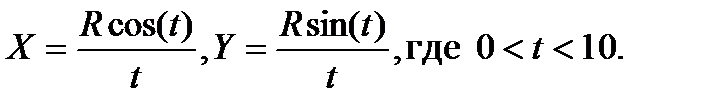
6. Построить график кривой, называемой «Декартов лист»:
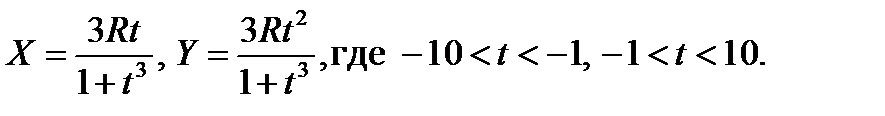
7. Построить график «конхоиды Никомеда»:
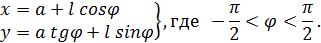
8. Построить график кривой, называемой «гипоциклоидой»:

9. Построить график кривой, называемой «спирограф»:
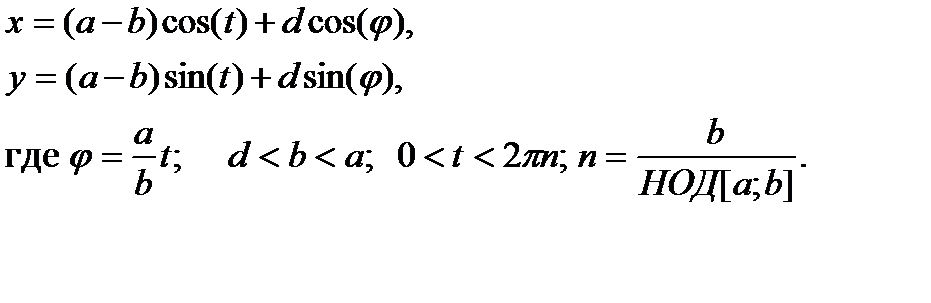
10. Построить график кривой, представляющей спираль с n витками:
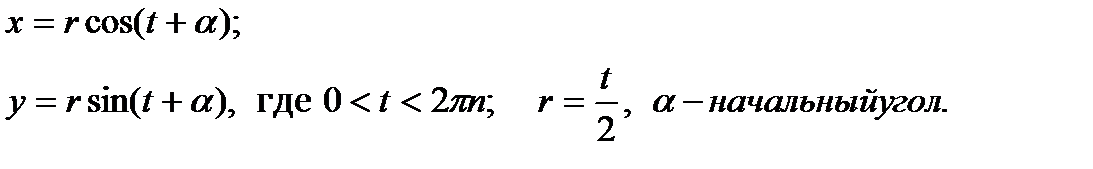
11. Построить график кривой, называемой «эпициклоида»:
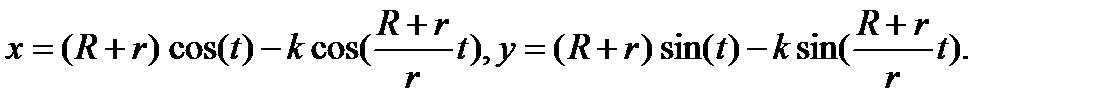
12. Построить график кривой, называемой «трактрисой»:
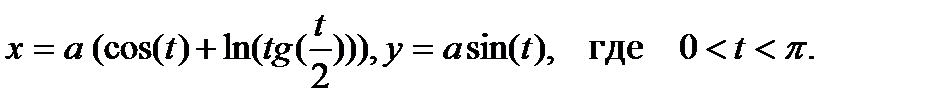
13. Построить график кривой, называемой «параболой Нейля»:

14. Построить график кривой, называемой «эвольвентой»:
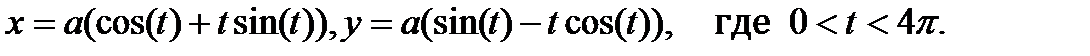
15. Построить график кривой, называемой «бабочкой»:
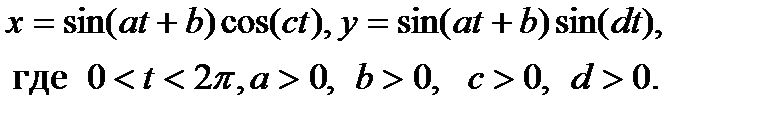
16. Построить график кривой, называемой «гипоциклоидой»:

17. Построить график кривой, называемой «улиткой Паскаля»:
 где -10 < t < 10.
где -10 < t < 10.
18. Построить график кривой, называемой «Декартов лист»:
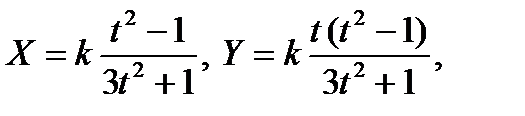
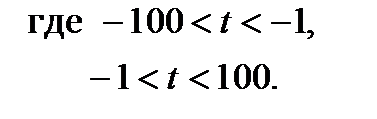
19. Построить график кривой, называемой «эвольвентой»:
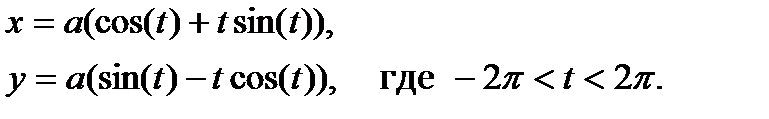
20. Построить график кривой, называемой «бабочкой»:
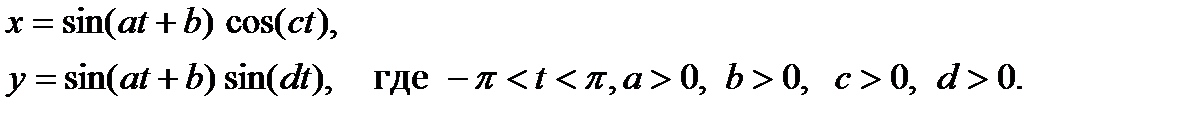
21. Построить график кривой, называемой «улиткой Паскаля»:
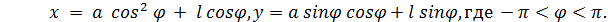
22. Построить график функции:
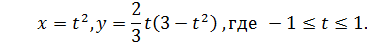
23. Построить график функции:
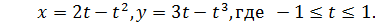
24. Построить график функции:
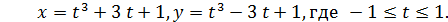
25. Построить график функции:
 при условии, что x изменяется на интервале
при условии, что x изменяется на интервале 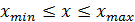 с шагом
с шагом  .
.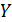 на отрезке
на отрезке 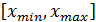 .
. , при
, при  и
и 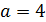 на интервале
на интервале 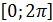 .
. в точке
в точке 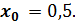
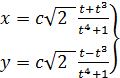 .
.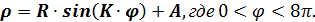
 , называемой ''ковбойская шляпа'':
, называемой ''ковбойская шляпа'': при
при  .
.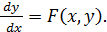
 и функции
и функции  при условии, что
при условии, что 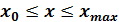 с шагом
с шагом 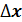 . Построить график решения дифференциального уравнения.
. Построить график решения дифференциального уравнения.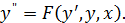
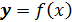 при условии, что
при условии, что  с шагом
с шагом  и при известных начальных условиях
и при известных начальных условиях  . Построить график решения дифференциального уравнения.
. Построить график решения дифференциального уравнения.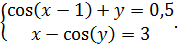
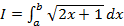 при a = 0и b = 1.
при a = 0и b = 1.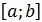 на n частей приводит к возможности рассмотрения площадей криволинейных трапеций на каждом небольшом отрезке
на n частей приводит к возможности рассмотрения площадей криволинейных трапеций на каждом небольшом отрезке  . Учитывая малую величину шага разбиения
. Учитывая малую величину шага разбиения 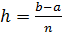 , площадь такой фигуры можно считать приближенно равной площади прямоугольника со сторонами
, площадь такой фигуры можно считать приближенно равной площади прямоугольника со сторонами 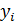 и h (рис.20).
и h (рис.20).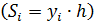 позволяет получить формулу "левых" прямоугольников
позволяет получить формулу "левых" прямоугольников
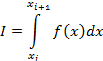
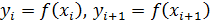 и высотой h
и высотой h 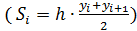 приводит после суммирования к следующей формуле
приводит после суммирования к следующей формуле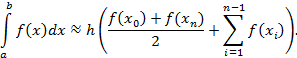
 отрезков позволяет на каждой паре отрезков
отрезков позволяет на каждой паре отрезков 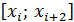 заменить подынтегральную функцию параболой
заменить подынтегральную функцию параболой 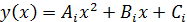 .
.
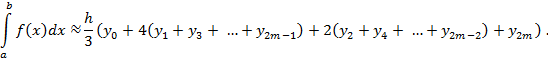
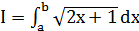 при a = 0 и b = 1.
при a = 0 и b = 1.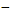 A4)/D4;
A4)/D4;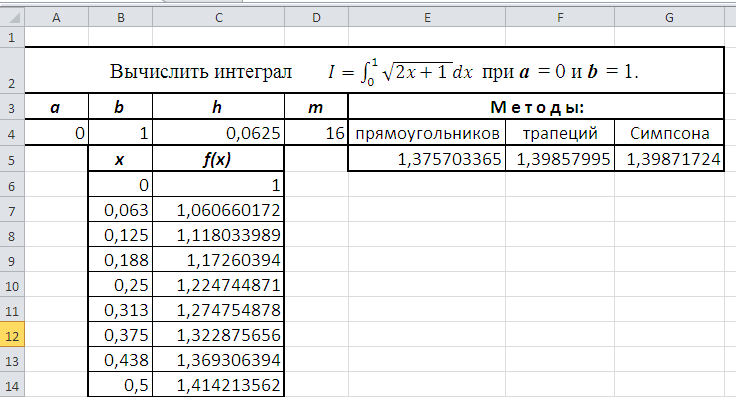
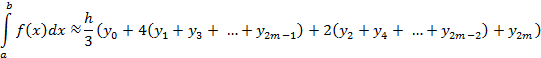

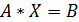 ,
,