Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к выполнению работы
Краткая справка Парной регрессией называется уравнение связи двух переменных y и x вида y = f (x), где y – зависимая переменная, функция; x –независимая переменная, аргумент. Различают линейные и нелинейные регрессии. Линейная регрессия описывается уравнением ŷ x = a + b · x. Среди нелинейных регрессийнаиболее часто применяются следующие модели: - гиперболическая ŷ x = a + b / x; - полиномиальная ŷ x = a + b · x + с · x 2; - показательная ŷ x = a · bx; - степенная ŷ x = a · xb; - экспоненциальная ŷ x = a · е bx; - логарифмическая ŷ x = a + b ·ln x и др. Построение уравнения регрессии. По имеющимся данным n наблюдений за совместным изменением двух параметров x и y {(xi, yi), i =1,2,…, n } необходимо определить аналитическую зависимость ŷ x = f (x), наилучшим образом описывающую данные наблюдений. Построение уравнения регрессии осуществляется в два этапа: - спецификация модели (определение вида аналитической зависимости ŷ x = f (x)); - оценка параметров выбранной модели. Спецификация модели. Парная регрессия применяется, если имеется доминирующий фактор, который и используется в качестве аргумента x в уравнении связи y = f (x). Применяется три основных метода выбора аналитической зависимости: - графический (на основе анализа поля корреляций); - аналитический, т.е. исходя из теории изучаемой взаимосвязи; - экспериментальный, т.е. путём сравнения средней ошибки аппроксимации Ā, рассчитанной для различных моделей регрессии (метод перебора). Оценка параметров модели. Для оценки параметров регрессий (a, b и c) используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений функции y от теоретических значений ŷ x при тех же значениях аргумента x минимальна, т.е.
Оценка тесноты связи. Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции rxy для линейной регрессии
где
Индекс корреляции ρ xy вычисляется по формуле
Долю дисперсии, объясняемую регрессией, в общей дисперсии переменной y характеризует коэффициент детерминации Коэффициент детерминации – квадрат коэффициента или индекса корреляции.Для оценки качества построенной модели регрессии можно использовать показатель (коэффициент, индекс) детерминации R 2 либо среднюю ошибку аппроксимации Средняя ошибка аппроксимации – среднее относительное отклонение расчётных значений от фактических. Чем выше показатель детерминации или чем ниже средняя ошибка аппроксимации, тем лучше модель описывает исходные данные. Построенное уравнение регрессии считается удовлетворительным, если значение Оценка значимости уравнения регрессии. Оценка значимости всего уравнения регрессии в целом осуществляется с помощью F-критерия Фишера. F -критерий Фишера заключается в проверке гипотезы Н0о статистической незначимости уравнения регрессии. Для этого выполняется сравнение фактического F факт и критического (табличного) F ma6л значений F -критерия Фишера. F факт определяется по следующей формуле
где п - число измерений; т - число параметров при переменных.Для линейной регрессии т = 1.Для нелинейной регрессии вместо F ma6л-максимально возможное значение критерия под влиянием случайных факторов при степенях свободы k 1 = т, k 2 = п - т - 1 (для линейной регрессии т = 1) и уровне значимости α. Определяется функцией Excel: =FРАСПОБР(α; k 1; k 2). Уровень значимости α - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно величина α принимается равной 0,05 или 0,01. Если F ma6л< F факт, то H 0 -гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F ma6л> F факт, то гипотеза Н0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Пример выполнения работы Построить уравнение регрессии между выходной толщиной h 1 и входной толщиной h 0 холоднокатаной полосы. Значения толщин x = h 0 и y = h 1 даны в таблице 2.
Регрессионный анализ в Excel невероятно прост. Как только данные представлены в графическом виде, регрессия выполняется с помощью нескольких щелчков мыши, поэтому регрессия с использованием прямой часто применяется, несмотря на то, что зависимость между переменными не линейная, а более сложная. Сформулируем практическое правило: всегда следует строить диаграмму, на которой представлена кривая регрессии и данные, чтобы можно было визуально оценить степень совпадения. В том случае, когда регрессия проводится с помощью линии тренда, кривая регрессии автоматически добавляется на диаграмму с соответствующими данными. Таблица 2
1. Подготовьте начальный рабочий лист с исходными данными (рис. 32), постройте точечную диаграмму. 2. При построении на диаграмме линии тренда Excel автоматически находит значения коэффициентов a и b, а также квадрат коэффициента корреляции (достоверность аппроксимации) R2. 3. Уравнение линии тренда и значение R2 по умолчанию на диаграмме не отображаются. Чтобы отобразить эту информацию, следует в нижней части диалога Параметры линии тренда поставить флажки в параметрах: þ показывать уравнение на диаграмме; þ поместить на диаграмме величину достоверности аппроксимации (R2).
Рис. 32. Исходные данные и точечная диаграмма
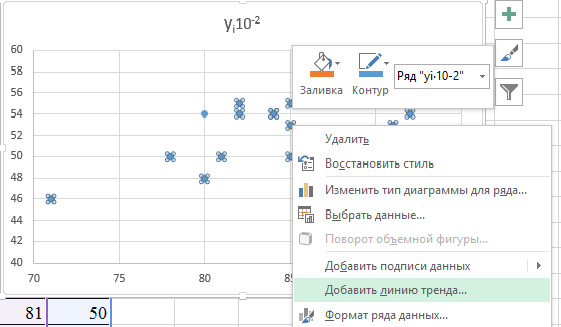
4. Щелкните правой кнопкой мыши на любом из маркеров данных и вконтекстном меню выберите команду Добавить линию тренда... (рис. 33).
Рис. 33. Контекстное меню
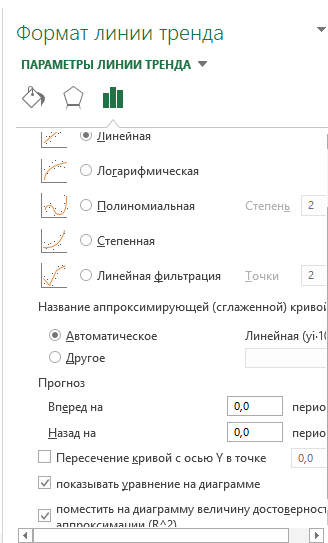
5. В диалоговом окне Параметры линии тренда выберите тип диаграммы Линейная (рис. 34). 6. Отобразите уравнение кривой регрессии на диаграмме, и величину достоверности аппроксимации (R 2).
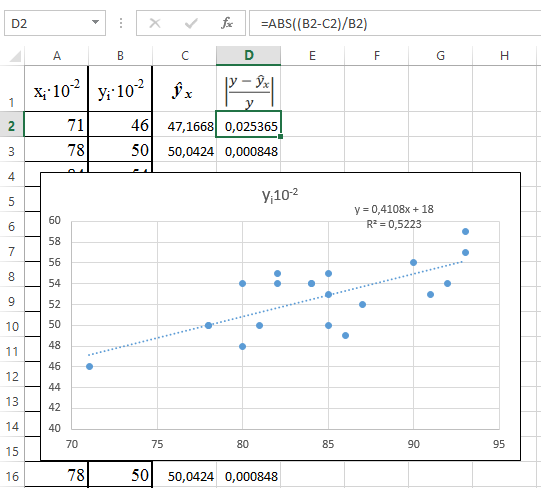
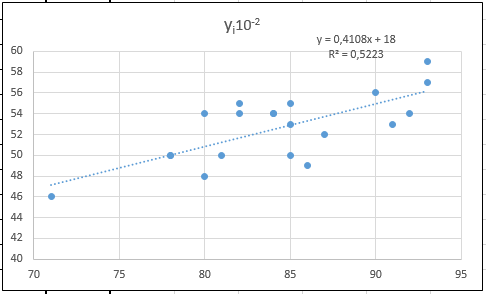
Рис. 34. Параметры линии тренда 7. Как видно из диаграммы (рис. 35), уравнение регрессии имеет вид y = 0,4108· х + 18 с достоверностью аппроксимации R 2 = 0,5223.
Рис. 35. Линейная модель 8. Рассчитаем среднюю ошибку аппроксимации, предварительно сформировав в столбце С массив значений в ячейку С2: = 0,4108*А2 + 18; в ячейку D2: =ABS((B2 – D2)/B2 (рис. 36).
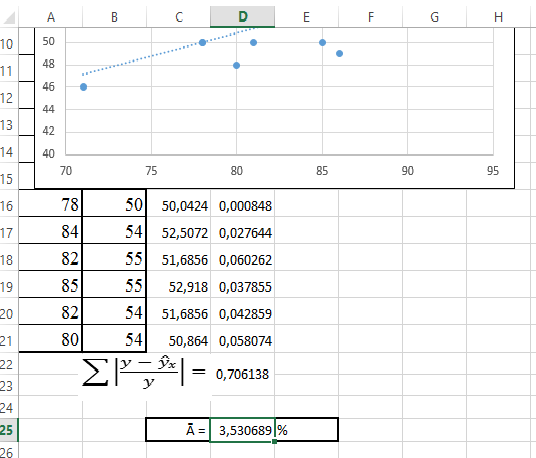
Рис. 36. Расчёт модельных значений и относительной ошибки 9. В ячейку D25 введите формулу: =1/20*D22*100 (рис. 37).
Рис. 37. Расчёт средней ошибки аппроксимации для линейной модели
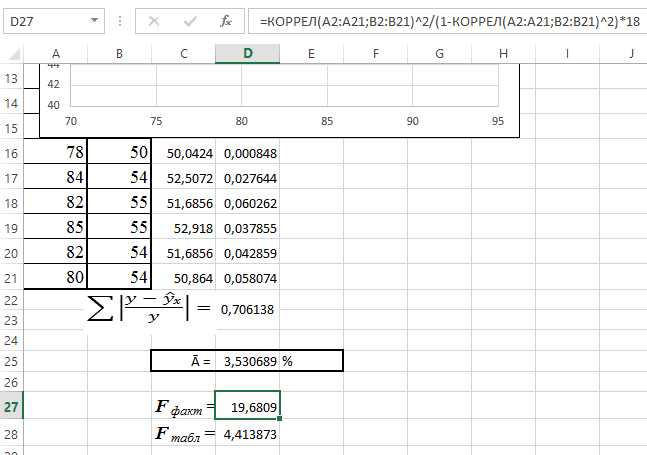
10. Рассчитайте F факт и F табл. Для этого в ячейки D27 и D28 введитеследующие формулы: D27: = КОРРЕЛ(A2:A21;B2:D21)^2/(1 -КОРРЕЛ(A2:A21;B2:D21)^2)*18; D28: = FРАСПОБР(0,05;1;18). Получаем F факт=19,6809, F табл=4,413873. Так как F ma6л< F факт, то H 0 - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность (рис. 37). Поскольку идеальной аппроксимации соответствует величина R 2 = 1, можно сделать вывод, что прямая линия не описывает зависимости идеально. Нужно попытаться подобрать другую кривую регрессии, обладающую некоторой кривизной.
Рис. 38. Расчёт фактического и табличного значения F-критерия Фишера
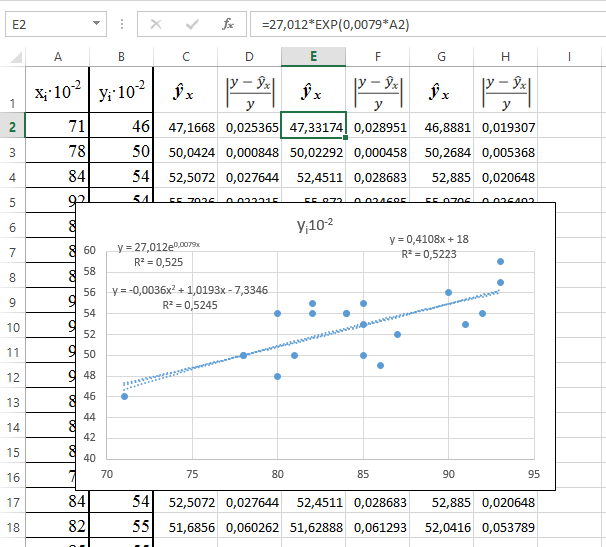
11. Рассчитаем параметры полиномиальной и экспоненциальной модели. Результаты моделирования и расчётов приведены на рис. 39 и 40.
12. В ячейку G2 введите формулу: = - 0,0036*А2^2 + 1,0193*A2 - 7,3346. Видно, что лучше всего экспериментальные данные описывает линейная зависимость, т.к. у линейной регрессии величина
Рис. 39. Параметры экспоненциальной аппроксимации
Рис. 40. Параметры параболической аппроксимации Лабораторная работа № 16 Множественная регрессия Задание На основании данных для соответствующего варианта: 1. Отобрать значимые аргументы для построения уравнения регрессии. 2. Построить уравнение линейной регрессии. 3. Определить коэффициент множественной корреляции. 4. Проверить значимость уравнения при уровнях значимости 0,05 и 0,01.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.13 (0.024 с.) |
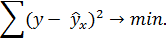
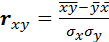 ,
,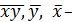 средние значения (функция Excel: =СРЗНАЧ(<диапазон>));
средние значения (функция Excel: =СРЗНАЧ(<диапазон>));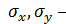 среднеквадратические отклонения (функция Excel:
среднеквадратические отклонения (функция Excel: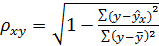 .
.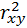 (для линейной регрессии) и индекс детерминации
(для линейной регрессии) и индекс детерминации 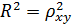 (для нелинейной регрессии).
(для нелинейной регрессии).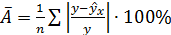 .
.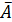 не превышает 10-12%.
не превышает 10-12%.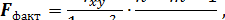
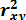 используется R 2.
используется R 2.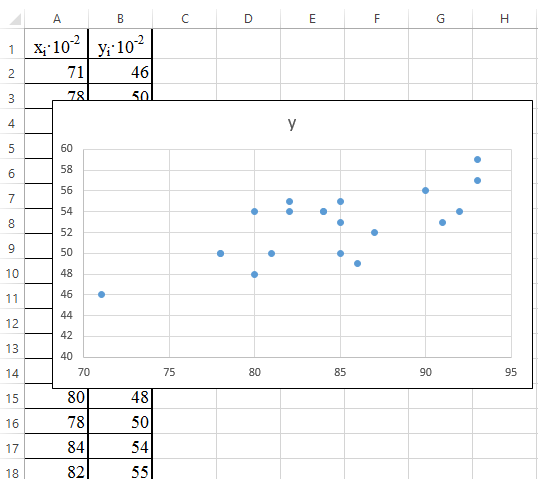
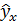 . Для этого введите следующие формулы:
. Для этого введите следующие формулы: