
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение формул приведения
Пример 8 2. Решите уравнение
Решение
Преобразуем уравнение:
Полученное уравнение - однородное, Разделим обе части уравнения на
Ответ:
Пример 8 3. Решите уравнение
Решение
Преобразуем уравнение, используя формулы приведения, получим:
Получим совокупность уравнений:
Ответ:
Пример 8 4. Решить уравнение
Решение
Преобразуем уравнение к однородному:
Полученное уравнение - однородное. Разделим обе части этого уравнения на Положим
Ответ:
Пример 8 5. Решить уравнение
Решение Это уравнение не является однородным. Перепишем его иначе:
Разделим обе части уравнения на Положим tgx = y, получим
Уравнение примет вид: Уравнение Ответ:
Пример 8 6. Решить уравнение Решение
Преобразуем уравнение: После приведения подобных слагаемых получим однородное уравнение третьей степени относительно sinx и cosx: Разделим обе части уравнения на Пусть tgx = y, тогда
Ответ:
Пример 8 7. Решить уравнение
Решение
Преобразуем уравнение:
Умножим левую часть уравнения на
Последнее уравнение - однородное четвертой степени относительно sinx и cosx.
Пусть
Задание 3
8 8. 90.
9 2. 9 4. 9 6. 9 7. 9 9. 101. 10 2. 10 3. 4. Для преобразования уравнений было использовано основное тригонометрическое тождество
отсюда находим
Далее,
Преобразуем сумму
Выше приведенные формулы очень часто используются при решении тригонометрических уравнений, и не только однородных.
Пример 10 5. Решите уравнение
Решение
Преобразуем уравнение, используя формулу (4): Пусть
Ответ: Пример 106. Решите уравнение
Решение Преобразуем уравнение, используя формулу (4):
Уравнение 2 - sin2x = 0, sin2x = 2 не имеет решений.
Ответ: Пример 107. Решите уравнение
Решение
Преобразуем уравнение, используя формулу:
Ответ:
Пример 108. Решите уравнение
Решение
Преобразуем уравнение, используя формулу:
Ответ:
Пример 10 9. Решите уравнение
Решение
Преобразуем уравнение, используя формулы:
получим:
Ответ:
Пример 1 10. Решите уравнение
Решение
Преобразуем уравнение, используя формулу (6)
Ответ:
Задание 4 111. 113. Метод замены переменных 4.1. Замена
Пусть дано некоторое тригонометрическое уравнение F(x) = 0. Обозначим через g(x) функцию Мы рассмотрим несколько случаев, когда это удается сделать. Введем (в некотором тригонометрическом уравнении) новое неизвестное
Ясно, что если уравнение содержит сумму функций
Если левая часть тригонометрического уравнения F(x) = 0 может быть выражена через
Пример 114. Решите уравнение
Решение
Пусть
Получим совокупность уравнений:
Ответ:
Замечание. Уравнение Аналогично решаются уравнения вида Здесь удобно положить Пример 115. Решите уравнение
Решение Й способ Положим
Ответ:
Й способ
Дальнейшее решение такое же, как и в первом способе. Применяя второй способ, мы обходимся без введения новых переменных и без подстановки, но использовать его может лишь опытный человек, который имеет достаточно большой навык в решении тригонометрических уравнений, искусственных преобразованиях и т. п.
Пример 116. Решите уравнение
Решение
Положим
Ответ:
Пример 117. Решите уравнение
Решение
Пусть
Ответ:
Пример 118. Решите уравнение
Решение
Положим
Ответ:
Пример 119. Решите уравнение
Решение
Пусть
Ответ: Пример 120. Решите уравнение
Решение
Область допустимых значений: Преобразуем уравнение:
Применим подстановку
|
||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 57; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.56.45 (0.157 с.) |
 .
.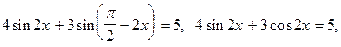




 приходим к уравнению:
приходим к уравнению: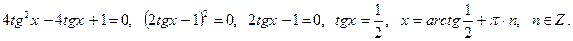

 .
.




 .
.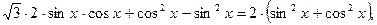
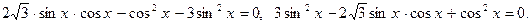
 (
(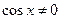 , ибо, в противном случае, из уравнения следует, что и
, ибо, в противном случае, из уравнения следует, что и 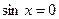 , что невозможно, так как тогда не будет выполняться основное тригонометрическое тождество
, что невозможно, так как тогда не будет выполняться основное тригонометрическое тождество 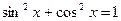 ). В результате деления на
). В результате деления на  .
. , получим
, получим 

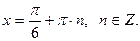
 .
. . Умножим левую часть уравнения на 1, а точнее на её значение
. Умножим левую часть уравнения на 1, а точнее на её значение  . После приведения подобных слагаемых имеем:
. После приведения подобных слагаемых имеем: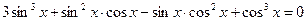 . Это однородное уравнение третьей степени относительно sinx и cosx,
. Это однородное уравнение третьей степени относительно sinx и cosx,  . Если cosx = 0, то из уравнения следует sinx=0, что невозможно.
. Если cosx = 0, то из уравнения следует sinx=0, что невозможно. , получим:
, получим: 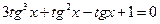 .
.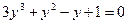 . Нетрудно заметить, что y = -1 является корнем уравнения. Разделим левую часть на y + 1, получим:
. Нетрудно заметить, что y = -1 является корнем уравнения. Разделим левую часть на y + 1, получим:
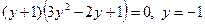 .
.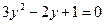 не имеет корней, так как дискриминант трехчлена отрицателен.
не имеет корней, так как дискриминант трехчлена отрицателен. 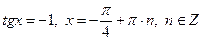 .
.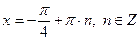
 .
. . Умножим левую часть уравнения на
. Умножим левую часть уравнения на  , получим:
, получим:  .
. ,
,  , получим:
, получим:  .
.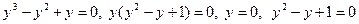 - не имеет корней.
- не имеет корней.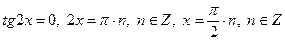 .
. .
. .
.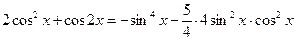 ,
, ,
, , получим:
, получим: ,
, ,
, ,
,  .
. , получим квадратное уравнение:
, получим квадратное уравнение:  ,
, .
.  - не удовлетворяет условию
- не удовлетворяет условию  и является посторонним корнем.
и является посторонним корнем.
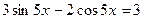 . 8 9.
. 8 9.  .
. . 9 1.
. 9 1.  .
. 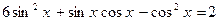 . 9 3.
. 9 3.  .
.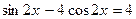 . 9 5.
. 9 5.  .
. .
. . 9 8.
. 9 8.  .
. . 100.
. 100.  .
. .
. .
. . 10 4.
. 10 4. 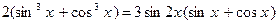 .
. . Это тождество не только позволяет сводить некоторые уравнения к однородным, но и в некоторых случаях дает возможность найти более простые решения таких уравнений. Для этой цели используются тождества, получаемые с помощью основного тригонометрического тождества.
. Это тождество не только позволяет сводить некоторые уравнения к однородным, но и в некоторых случаях дает возможность найти более простые решения таких уравнений. Для этой цели используются тождества, получаемые с помощью основного тригонометрического тождества.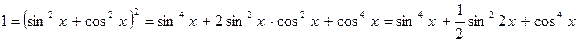 ,
, .
.
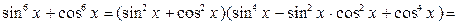
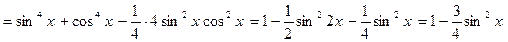 .
.
 , используя формулу (4).
, используя формулу (4).

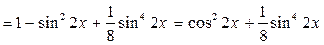 .
.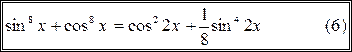
 .
.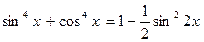 , получим уравнение:
, получим уравнение:  .
. приходим к квадратному уравнению:
приходим к квадратному уравнению: ,
,
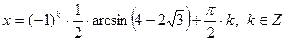 .
. .
.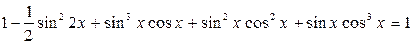 ,
,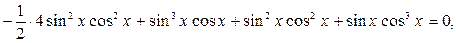
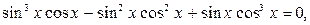
 ,
, .
. .
.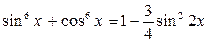 , получим:
, получим: 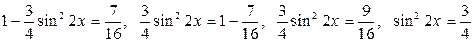


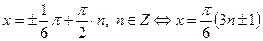 .
.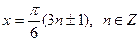 .
. .
.
 .
.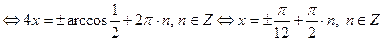
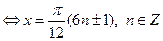 .
. .
.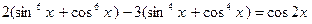 .
. и
и  ,
, ,
, .
.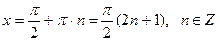 .
. .
.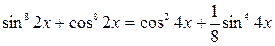 , получим уравнение:
, получим уравнение:
 . Пусть
. Пусть  , получим:
, получим:

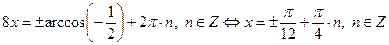 .
.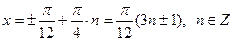 .
. . 112.
. 112.  .
. .
.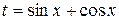 .
.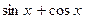 и введем новое неизвестное
и введем новое неизвестное  . Если удастся выразить функцию F(x) через t, т. е. представить ее в виде
. Если удастся выразить функцию F(x) через t, т. е. представить ее в виде  , то решение уравнения F(x) = 0 будет сведено к решению уравнения f(t) = 0. Разумеется, не всегда левую часть F(x) удается достаточно просто выразить через
, то решение уравнения F(x) = 0 будет сведено к решению уравнения f(t) = 0. Разумеется, не всегда левую часть F(x) удается достаточно просто выразить через  .
.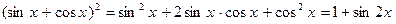 , находим
, находим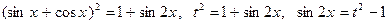 .
. , тогда его можно выразить через t.
, тогда его можно выразить через t. ,
,  .
. .
. .
. .
.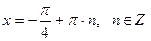 .
.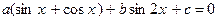 имеет решения в том и только в том случае, когда дискриминант уравнения
имеет решения в том и только в том случае, когда дискриминант уравнения 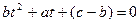 неотрицателен и по крайней мере один из корней этого уравнения удовлетворяет условию
неотрицателен и по крайней мере один из корней этого уравнения удовлетворяет условию  , так как
, так как  .
. .
. и тогда
и тогда 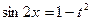 .
. .
.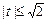 , получим уравнение:
, получим уравнение: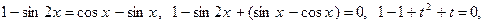
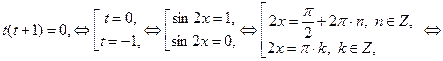


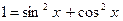 :
: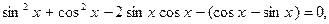
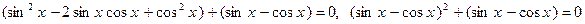 ,
,
 .
. , получим уравнение:
, получим уравнение:
 .
. .
. .
.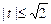 получим квадратное уравнение:
получим квадратное уравнение: 
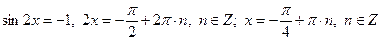 ;
; .
. .
.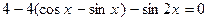 .
. - не удовлетворяет условию
- не удовлетворяет условию  .
.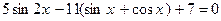 .
.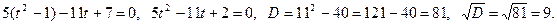
 - не удовлетворяет условию
- не удовлетворяет условию  ,
, .
.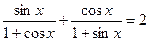 .
.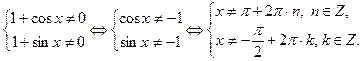
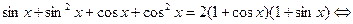
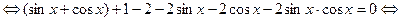
 .
. , тогда
, тогда 
 , получим уравнение
, получим уравнение




