
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волгодонский инженерно-технический институт - филиал нияу мифиСтр 1 из 4Следующая ⇒
Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
Методические указания по теме:
«Линейная, векторная алгебра и аналитическая геометрия» Волгодонск
Определители матрицы. Системы линейных алгебраических уравнений. Определители и их свойства. Вычисления определителей. Определителем n-го порядка называется число
Любую строку или столбец определителя называют рядом. Главной диагональю определителя называется совокупность элементов Минором Алгебраическое дополнение Правила вычисления Для n=2 Для n=3 Для произвольного n Например:
Перечислим основные свойства определителей: 1. Сумма произведений элементов любого ряда определителя и их алгебраических дополнений не зависит от номера ряда и равна этому определителю.
Эти равенства (как и формулу (1)) можно считать правилом вычисления определителя. Первое из них называется разложением 2. значение определителя не меняется после замены всех его строк соответствующими столбцами и наоборот; 3. если поменять местами два параллельных ряда определителя то он изменит знак на противоположный; 4. определитель с двумя одинаковыми параллельными рядами равен нулю; 5. если все элементы некоторого ряда определителя имеют общий множитель, то последний можно вынести за знак определителя; 6. если все элементы какого-либо ряда определителя равны нулю, то определитель так же равен нулю; 7. определитель, у которого элементы двух параллельных рядов соответственно пропорциональны, равен нулю; 8. определитель не измениться, если ко всем элементам какого-либо ряда прибавить соответствующие элементы другого параллельного ряда, умноженные на одно и то же произвольное число.
Методы решения систем линейных алгебраических уравнений. Метод Крамера. Если для системы n уравнений с n неизвестными
Матричный метод. Рассмотрим систему n уравнений с n неизвестными (2). Обозначим
Тогда система (2) может быть записана в матричной форме: АХ=В Умножив это матричное уравнение слева на
Следовательно, чтобы найти матрицу-решение Х, надо найти Надо помнить, что для матрицы А существует единственная обратная матрица Метод Гаусса. Рассмотрим систему m уравнений с n неизвестными
Введем обозначение:
С помощью элементарных преобразований матрица Далее записываем систему уравнений, соответствующих последней матрице, эквивалентной исходной. Двигаясь снизу вверх, последовательно находим неизвестные. Метод Гаусса позволяет решать системы, имеющие единственное решение, бесконечное множество решений и определять, что система решений не имеет. Историческая справка. Метод последовательного исключения неизвестных для нахождения решений системы линейных уравнений опубликован в 1849 году немецким математиком, физиком и астрономом Карлом Фридрихом Гауссом (1777-1855). Но уже во 2 в. до н.э. в Китае был известен метод «фан-чен» решение системы n линейных уравнений с n неизвестными, по существу совпадающий с методом Гаусса, от которого он отличается тем, что все операции проводится на счетной доске (само название «фан-чен» переводится как «выстраивание чисел по клеткам»). Правильное расположение чисел на доске заменяло китайскому математику буквы и индексы нашей символики.
Решение типового варианта. Задача 1. Даны матрицы А, В, С, числа Вычислить: а)
а)
б)
в)
=-35-4+21-16+5(3+20)=-55+21+115=81 Найдем алгебраические дополнения
Присоединенная матрица
Обратная матрица
Проверка:
Обратная матрица найдена верно.
Задача 2. Решить системы линейных уравнений а) по формулам Крамера, матричным методом, методом Гаусса; б) методом Гаусса; в) методом Гаусса.
а)
Решение: а) 1. Решим систему методом Крамера.
=2+1-2(4+1)-(-2+1)=3-10+1=-6
=5(2+1)-2(8+3)-(-4+3)=15-22+1=-6
=8+3-5(4+1)-1(-6+4)=11-25+2=-12
=-3+4-2(-6+4)+5(-2+1)=1+4-5=0
Чтобы проверить решение, подставим в исходную систему уравнений найденные значения неизвестных.
Получены верные равенства, система решена правильно. Ответ: x=1, y=2, z=0.
2. Решим систему матричным методом.
Запишем систему уравнений в матричном виде: AX=B. Умножим обе части уравнения слева на
Найдем алгебраические дополнения
Присоединенная матрица
Обратная матрица
Ответ: x=1, y=2, z=0. 3. Решим систему методом Гаусса.
Запишем расширенную матрицу и элементарными преобразованиями сведём её к «треугольному» виду:
«2 стр.» + «1 стр.» «3 стр.» + «1 стр.»
«3 стр.» + «2 стр.» Полученной матрице соответствует следующая система уравнений:
Решим уравнения, двигаясь снизу вверх 1) 2z=0 2) -y+z=-2 3)x+2y-z=5 z=0 -y+0=-2 x+4-0=5 y=2 x=1 Ответ: x=1, y=2, z=0.
б) Решим систему методом Гаусса.
«2 стр.» + «1 стр.» «3 стр.» + «1 стр.»
Система n-m=3-2=1 Одно неизвестное обозначим как произвольный параметр t, оставшиеся 2 через него выразим.
Пусть z=t тогда -y+5t=-2 x+y-2z=3 -y=-5t-2 x+5t+2-2t=3 y=5t+2 x=1-3t Бесконечное множество решений системы запишем следующим образом:
Покажем, что формулы нахождения решений получены правельно. Пусть t=0, тогда
Получили верные равенства, значит решение выполнено правильно. Ответ: Система имеет бесконечное множество решений: в)
«2 стр.» + «1 стр.» «3 стр.» + «1 стр.»
Матрице соответствует следующая система уравнений:
Последнее уравнение не имеет решений ни при каких значениях x,y,z, значит и система решений не имеет. Ответ: Система не имеет решений. Векторная алгебра. Аналитическая геометрия. Уравнения плоскости. 1.Уравнение плоскости, проходящей через точку Пусть
2.Общее уравнение плоскости:
Вектор 3.Уравнение плоскости в отрезках на осях:
Пусть заданы две плоскости Ax+By+Cz+D=0 и
1.Угол, образованный двумя плоскостями равен углу между их нормальными векторами:
2.Условие параллельности плоскостей
3.Условие перпендикулярности плоскостей:
Расстояние точки
Общее уравнение прямой
Задача№3. Даны координаты точек A,B,C,D. Найти: а) угол между векторами б) площадь треугольника АВС; в) высоту треугольника АВС, опущенную из вершины С; г) объем пирамиды ABCD; д) высоту пирамиды ABCD, опущенную из вершины D на основание АВС. А(-1,2,3), В(4,-1,3), С(2,0,5), D(7,8,-1) Решение: а)
б) Площадь треугольника АВС, построенного на векторах
в) Известно, что г)
=5(8-12)+3(-12-16)=-20-84= - 104
д) Задача №4. Составить уравнение плоскости проходящей через точку А и перпендикулярно вектору
Решение.
Пусть точка M(x,y,z) – произвольная точка искомой плоскости, 2x-y+3z+8=0 - уравнение искомой плоскости. Задача №5. Даны координаты точек A,B,C,D. Найти: а) уравнение плоскости, проходящей через точки А,В,С; б) расстояние точки D до плоскости АВС; в) угол между плоскостью АВС и плоскостью 5x-3y+7z-3=0 А(1;1;3), В(-2;1;4), С(-1;2;3), D(-1;1;5). Решение: а) В искомой плоскости возьмём некоторую точку M(x,y,z), тогда вектора
Запишем условие компланарности трёх векторов (см. 2.1.4.):
(x-1)(0-1)-(y-1)(0+2)+(z-3)(-3+0)=0 -x+1-2y+2-3z+9=0 X+2y+3z-12=0 – уравнение плоскости АВС, её нормальный вектор б) Найдем расстояние точки D до плоскости АВС. (см. 2.2.1. формула (4))
в) угол между плоскостями равен углу между их нормальными векторами
Задача №6. Прямая Найти: а) канонические и параметрические уравнения прямой б) найти угол между прямой Решение: а) Прямая Направляющий вектор прямой
Для простоты возьмём направляющим вектором противоположный
Пусть z=0, тогда
Тогда параметрические уравнения прямой
б) Угол между прямыми
Задача №7. Найти точку пересечения прямой и плоскости. Найти угол между прямой и плоскостью. Решение: Уравнения прямой запишем в параметрическом виде (см. 2.2.2):
2(t+1)+3(-2t-1)+6t-1=0, 2t+2-6t-3+6t-1=0, 2t=2, t=1. Чтобы найти точку пересечения прямой и плоскости
Задача №8. Даны координаты точек А,В,С. Найти: а) уравнение медианы AD; б) уравнение высоты АЕ; в) угол между AD и АЕ; г) уравнение прямой, проходящей через точку С параллельно АВ. А (-4;2), В (6;-4), С (4;10). Решение: а) Точка D – середина отрезка ВС, её координаты (см. 2.1.1.):
Уравнение медианы AD находим как уравнение прямой, проходящей через две точки (см. (11) в пункте 2.2.3.).
б) Чтобы найти уравнение высоты АЕ, составим уравнение перпендикулярной ей СВ (см. (11)).
-7(x-6)=y+4, y=-7x+38 - уравнение СВ,
в) По формуле (13) пункта 2.2.3 найдем угол между АЕ и AD, в нашем случае г) Найдем уравнение прямой АВ (см. (11)
Искомая прямая Запишем уравнение пучка прямых, проходящих через точку С: y-10=k(x-4) и подставим вместо k значение y-10=-0,6(x-4) y=-0,6x+12,4 уравнение прямой СМ. Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
Методические указания по теме:
«Линейная, векторная алгебра и аналитическая геометрия» Волгодонск
|
||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 58; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.183.150 (0.189 с.) |
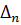 , записанное в виде квадратной таблицы
, записанное в виде квадратной таблицы
 , где i-номер строки, j- номер столбца, на пересечении которых располагается
, где i-номер строки, j- номер столбца, на пересечении которых располагается 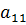 ,
,  , …
, …  .
. элемента
элемента  полученный из определителя n-го порядка вычеркиванием i-й строки и j-го столбца.
полученный из определителя n-го порядка вычеркиванием i-й строки и j-го столбца. элемента
элемента 

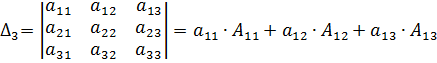
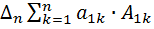 (1)
(1)
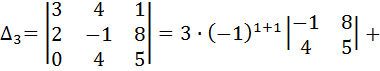
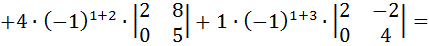
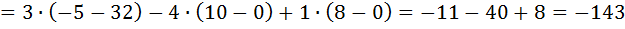
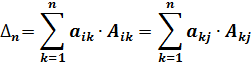
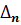 по его элементам i -той строки, а второе- разложением
по его элементам i -той строки, а второе- разложением 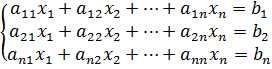 (2)
(2) ,
, 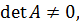 то система (2) имеет единственное решение, которое находится по формулам Крамера:
то система (2) имеет единственное решение, которое находится по формулам Крамера: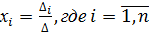 ,
,  - определители n-го порядка, которые получаются из
- определители n-го порядка, которые получаются из  путем замены i-го столбца столбцом свободных членов
путем замены i-го столбца столбцом свободных членов 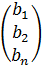 исходной системы.
исходной системы.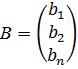 - матрица-столбец свободных членов,
- матрица-столбец свободных членов, 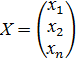 - матрица столбец неизвестных.
- матрица столбец неизвестных. , получим:
, получим: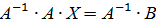 т.к.
т.к. 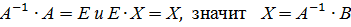
 , если
, если  , т.е. матрица не вырожденная.
, т.е. матрица не вырожденная.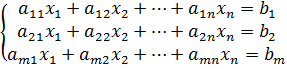 (3)
(3) - расширенная матрица для системы (3)
- расширенная матрица для системы (3) сводится к «треугольному» виду, т.е. под элементами главной диагонали должны быть нули.
сводится к «треугольному» виду, т.е. под элементами главной диагонали должны быть нули.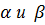 .
.
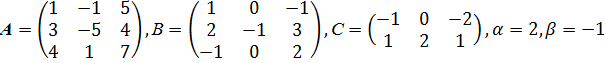

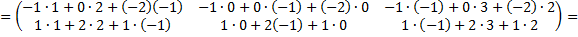
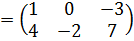
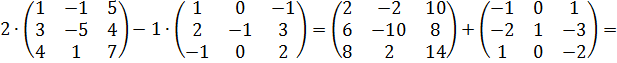
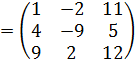


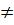 0
0
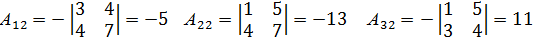
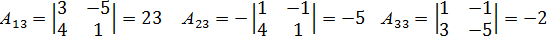
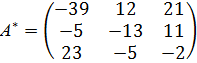
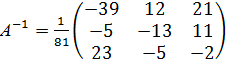
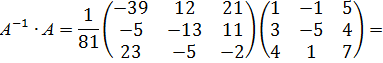
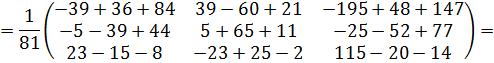


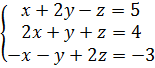




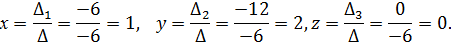


 - основная матрица
- основная матрица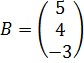 – матрица-столбец свободных членов
– матрица-столбец свободных членов - матрица-столбец неизвестных
- матрица-столбец неизвестных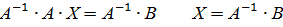
 .
.


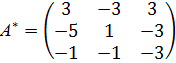
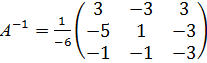
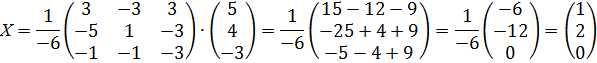

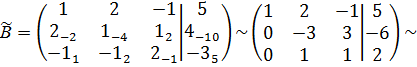
 (-2) «2 стр.»
(-2) «2 стр.»  3
3

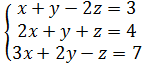


 имеет бесконечное множество решений, количество уравнений (m=2) меньше чем количество неизвестных (n=3).
имеет бесконечное множество решений, количество уравнений (m=2) меньше чем количество неизвестных (n=3). где
где  .
. подставим в исходную систему:
подставим в исходную систему: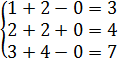
 Решим систему методом Гаусса.
Решим систему методом Гаусса.
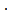 (-2) «3 стр.» + «2 стр.»
(-2) «3 стр.» + «2 стр.» 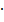 (-1)
(-1)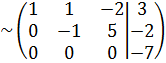
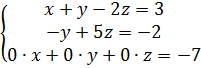
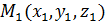 и перпендикулярной к вектору
и перпендикулярной к вектору  .
.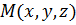 произвольная точка плоскости,
произвольная точка плоскости,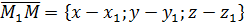
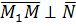 и по условию ортогональности векторов (см. 2.1.2.)
и по условию ортогональности векторов (см. 2.1.2.) (1)
(1) (2)
(2)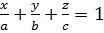 (3)
(3)



 от плоскости Ax+By+Cz+D=0:
от плоскости Ax+By+Cz+D=0:

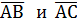 ;
;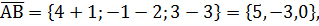
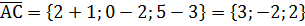
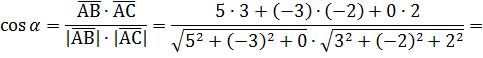

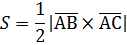



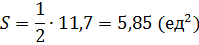
 , значит
, значит 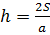 ,
, 

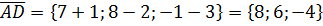
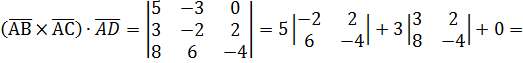
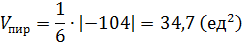
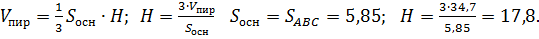
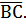 А(1;4;-2), B(6;7;0), C(8;6;3).
А(1;4;-2), B(6;7;0), C(8;6;3). – нормальный вектор к искомой плоскости (см. 2.2.1.)
– нормальный вектор к искомой плоскости (см. 2.2.1.)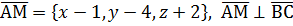 и по условию перпендикулярности векторов 2(х-1)+(-1)(y-4)+3(z+2)=0, 2x-2-y+4+3z+6=0,
и по условию перпендикулярности векторов 2(х-1)+(-1)(y-4)+3(z+2)=0, 2x-2-y+4+3z+6=0, 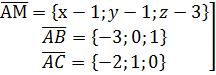 лежат в искомой плоскости, значит компланарны.
лежат в искомой плоскости, значит компланарны.

 .
.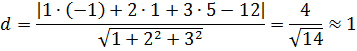
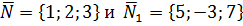


 задана общими уравнения.
задана общими уравнения.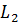 :
: 

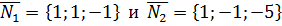 .
. ортогонален
ортогонален 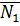 и
и  , найдем его как векторное произведение (см. 2.1.3).
, найдем его как векторное произведение (см. 2.1.3).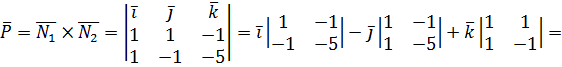

 Найдем какую-нибудь точку, лежащую на
Найдем какую-нибудь точку, лежащую на  Сложим уравнение, получим 2х=8, х=4, значит y=-4. Точка
Сложим уравнение, получим 2х=8, х=4, значит y=-4. Точка 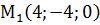 принадлежит искомой прямой, параллельной вектору
принадлежит искомой прямой, параллельной вектору 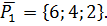 Пусть точка M(x,y,z) некоторая точка искомой, тогда вектор
Пусть точка M(x,y,z) некоторая точка искомой, тогда вектор  коллинеарен вектору
коллинеарен вектору 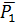 . Запишем условие коллинеарности двух векторов (см.2.2.2)
. Запишем условие коллинеарности двух векторов (см.2.2.2)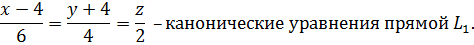

 равен углу между их направляющими векторами
равен углу между их направляющими векторами 

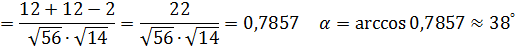
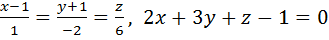
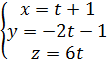 Выражения подставим в уравнения плоскости, решим его относительно t:
Выражения подставим в уравнения плоскости, решим его относительно t: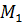 , подставим найденное значение t в параметрические уравнения, получим x=2, y=-3, z=6, т.е.
, подставим найденное значение t в параметрические уравнения, получим x=2, y=-3, z=6, т.е.  Угол
Угол 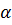 между прямой и плоскостью находим по формуле (9) пункта 2.2.2. Направляющий вектор прямой
между прямой и плоскостью находим по формуле (9) пункта 2.2.2. Направляющий вектор прямой  , нормальный вектор плоскости
, нормальный вектор плоскости  .
.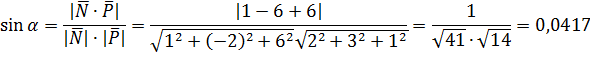
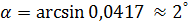

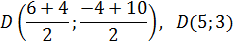
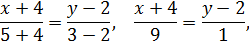

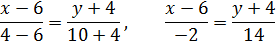
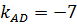

 и поставим вместо k значение
и поставим вместо k значение 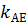


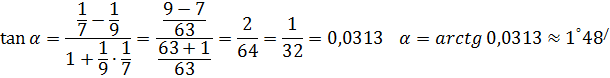

 (см. (15) пункт 2.2.3)
(см. (15) пункт 2.2.3)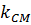 .
.


