
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математический пакет MathCADСодержание книги Поиск на нашем сайте
Методические указания по проведению учебно-технологической практики (УТП) в группах первого курса
Математический пакет MathCAD
Москва, 2016 Цель преподавания УТП – содействие формированию профессиональных компетенций при проведении инженерных расчетов с использованием математического пакета MathCAD в общепрофессиональной, производственно-технологической и научно-исследовательской деятельности. Задачами преподавания УТП являются освоение: - основных возможностей пакета; - первичных навыков построения и вычисления выражений, редактирования объектов, работы с дискретными переменными, таблицами, графиками; - первичных навыков программирования; - первичных навыков символьных вычислений, дифференцирования и интегрирования выражений; - правил техники безопасности и внутреннего распорядка. Прохождение распределенной практики (практикума) заключается в проведении аудиторных занятий с предоставлением каждому студенту индивидуального рабочего места, оборудованного персональным компьютером с программным обеспечением, и самостоятельной работы студентов над учебным пособием и указанной литературой по дисциплине. Во время аудиторных занятий проводятся индивидуальная и коллективная консультации студентов с преподавателем. Основные сведения о MathCAD MathCAD – инструмент для работы инженеров, мощный калькулятор, имеющий следующие преимущества: - запись математических выражений в обычном инженерном виде; - простота использования; - возможность создания качественных технических отчетов с таблицами, графиками, текстом; - дискретная переменная, позволяющая вычислять одновременно функцию для целого ряда аргументов. Рабочее окно MathCAD выглядит аналогично другим Windows приложениям. Главное меню – верхняя строка рабочего окна. В нём можно выполнить любые действия. Панели инструментов – для быстрого выполнения часто применяемых команд: - стандартная для действий с файлами, редактирования, вставки; - форматирования текста и документов; - математическая для вставки математических символов и операторов. Нажатие кнопок математической панели открывает дополнительные панели, с помощью которых можно вставить в документ символ или шаблон операции. При наведении указателя мыши на кнопки панели инструментов появляются всплывающие подсказки с названием операции и сочетанием клавиш, нажатие которых эквивалентно щелчку на данной кнопке. Построение графиков В MathCAD доступно построение семи основных типов графиков, два из которых относятся к категории двумерных (декартовые и полярные), остальные трёхмерные. Создание графической области возможно несколькими способами: - через главное меню «вставить» · «графики» · выбор нужного типа; - щелчком на кнопке нужного типа графика панели «Графики» математической панели; - нажатием на клавишу @ в английской раскладке клавиатуры. Рассмотрим построение двумерного “X-Y” графика как наиболее распространённого. В появившемся шаблоне двумерного графика на оси абсцисс необходимо ввести имя аргумента, а на оси ординат имя функции или выражение, содержащее аргумент и определённые заранее константы. Если затем щёлкнуть мышью вне шаблона графика, то появится график функции или выражения в пределах значений аргумента от – 10 до +10. Другой (требуемый) диапазон изменения значений аргумента может быть установлен принудительным введением соответствующих значений в маркерные позиции по оси абсцисс. Аналогично может быть изменён диапазон значений по оси ординат. При необходимости размещения графиков нескольких функций или выражений следует ввести имена функций или выражения на оси ординат. Для этого необходимо поместить синий уголок курсора в конец первого имени на графике и нажать клавишу, (запятая) В появившемся месте ввода необходимо вписать имя второй функции или второе выражение и т.д. Для двух функций, имеющих разные аргументы, необходимо на оси ординат ввести имена обеих функций, а на оси абсцисс имена обоих аргументов. Если функций на графике больше двух, а аргументов два, то график первой функции будет построен по первому аргументу, а остальных функций – по второму. Введение по осям ординат и абсцисс имён двух функций одного аргумента приводит к построению параметрического графика. На одном графике можно помещать до 16 функций. Для придания графику желаемого вида его необходимо отформатировать. Двойной щелчок указателем мыши в области графика приводит к открытию диалогового окна форматирования графика, с помощью которого можно существенным образом изменять внешний вид графика, меняя вид, цвет и толщину линий, вводя на график сетку и метки. Изменение размера и перемещение графика можно осуществить обычным растягиванием его рамки или перетаскиванием с помощью мыши. Для создания трёхмерного графика, также как и в случае двумерного, необходимо создать графическую область одним из способов: - через главное меню «вставить» · «графики» · выбор нужного типа; - щелчком на кнопке нужного типа графика панели «Графики» математической панели; - одновременным нажатием на клавиши Ctrl и 2 при любой раскладке клавиатуры. В появившемся шаблоне вместо единственного выделенного курсором маркера необходимо ввести сокращённое имя функции (без скобок и перечисления переменных) или имя сформированного заранее массива, для которых будет строиться график. В отличие от двумерного графика в позиции маркера запись выражения не допускается. Первоначально график строится в пределах изменения аргументов от –5 до +5. Двойной щелчок указателем мыши в области графика приводит к открытию диалогового окна форматирования, с помощью которого ему можно придать желаемый вид. Работа с массивами Массивами (arrays) называют упорядоченные последовательности чисел или элементов массива. Доступ к любому элементу массива возможен по его индексу (номеру). В MathCAD условно выделяются два типа массивов: - векторы (одно индексные), матрицы (двух индексные) и тензоры (многоиндексные) массивы; - дискретные (ранжированные) переменные (range variables) – векторы, элементы которых определенным образом зависят от их индекса. Имя массива задаётся также как и имя выражения, но в отличие от последнего может иметь один или несколько индексов. Например, если А – это заданный ранее вектор, то введение символов “А” и “=” приведёт к выводу всех значений этого вектора. В MathCAD имеются операторы и встроенные функции, которые действуют на векторы и матрицы целиком, например, транспонирование, матричное умножение, вычисление определителя и т. д. Над элементами массива можно совершать действия как над обычными числами. Для действий над одним элементом вектора А должен быть указан его индекс, например запись А3 однозначно определяет третий элемент этого вектора. Нужно только правильно задать соответствующий индекс или сочетание индексов массива. Например, чтобы получить доступ к нулевому элементу вектора А, нужно ввести имя переменной массива (А), нажать кнопку Subscript (нижний индекс) со значком хn на панели Matrix (Матрица) либо ввести [. В появившийся справа снизу от имени массива место заполнитель вводится желаемый индекс (0). Если после этого ввести знак численного вывода, то справа от него появится значение нулевого элемента вектора. Для двух знаковой индексации и более индексы указываются через запятую. Начало нумерации элементов в векторах и матрицах определяется встроенной переменной ORIGIN. По умолчанию ORIGIN = 0, т.е. первые элементы столбцов и строк имеют нулевой индекс. Такую индексацию можно изменить, например, набрав прописными буквами строку ORIGIN = 1 или другим способом. Необходимо помнить, что некоторые встроенные функции MathCAD по умолчанию подразумевают наличие нулевого индекса. Существует три способа создания массива: - заполнение шаблона матрицы, содержащего пустые места для ввода чисел («вставить» · «матрица») с выбором количества строк и столбцов; - использование дискретной переменной, что удобно при наличии формулы для вычисления элементов массива; - считывание данных из файла. Существует ещё один способ создания матрицы (вектора). В необходимом месте листа набираем имя массива с соответствующей индексацией в виде конкретных чисел или букв, которые, впрочем, должны быть определены заранее, и присваиваем ему значение ноль. Например, А9:= 0. При этом будет сформирован вектор А из девяти элементов и всем его элементам будут присвоены нулевые значения. Далее можно вывести полученный массив на лист и вместо нулей ввести требуемые значения. При вводе больших векторов для экономии места удобно формировать их в виде строки. Однако матричные операторы и функции работают только со столбцами, а не строками, поэтому для выполнения действий со строками их надо транспонировать, а после выполнения операций вновь транспонировать в столбцы. Транспонирование – операция, преобразующая столбцы исходной матрицы в строки, а строки в столбцы. Для считывания данных из файла в MathCAD используется функция READPRN(“file”), где “file” – имя файла или путь к нему, если он находится в другом каталоге. Функция WRITEPRN(“file”) осуществляет запись числовых данных в файл. Функция sort(A) позволяет осуществить сортировку элементов вектора А в порядке возрастания, а функция reverse (A) – в порядке убывания. Операции сложения, вычитания, умножения и деления, применённые к имени массива без индексации его элементов и числу z, приводят к соответствующим действиям с каждым элементом массива. Например, оператор A+z приводит к сложению каждого элемента массива А с числом z. Двойной щелчок в области отображения массива вызывает меню форматирования результата, с помощью которого можно придать массиву желаемый вид. Решение уравнений Для решения уравнений вида Точность полученного решения зависит от значения встроенной константы TOL, определяющей точность численных методов. По умолчанию TOL = 0,001. Она может быть изменена пользователем, но следует знать, что чем меньше величина этой константы, тем больше времени затрачивается на вычисления. Если уравнение неразрешимо, то выдаётся сообщение об ошибке. К ошибке может приводить также поиск решения в области локальных экстремумов или при выборе начального значения слишком далеко от реального решения, что связано с особенностью используемого численного метода (метод секущих). Таким образом, функция root требует некоторой априорной информации о корнях исследуемой функции. В случае, если исследуемая функция Первой строкой вводится вектор v, состоящий из (n+1) элемента. На первом месте у этого вектора должен стоять свободный член, далее коэффициенты полинома в порядке возрастания степени. После этого вызывается встроенная функция polyroots(v), выдающая результат в виде вектора, содержащего n корней полинома. Вычисления проводятся численными методами, их точность определяется той же встроенной константой TOL, которая может изменяться пользователем. Корни полинома могут быть комплексными, а погрешность, определяемая константой TOL касается как действительной, так мнимой частей получаемого корня. Пусть имеется система нелинейных уравнений:
где каждая - вводится ключевое слово Given; - решаемая система записывается с помощью Булевых операторов равенства и, если потребуется, неравенства; - некоторому вектору (например v) присваиваются значения встроенной функции Обращение к этому вектору ( При использовании этой процедуры необходимо учитывать следующие особенности: - предварительно, до ключевого слова Given всем переменным - функции - поиск решения проводится численными методами, и погрешность результата при решении системы будет определяться встроенной константой CTOL, которую пользователь может менять (по умолчанию CTOL = 0,001); - при попытке решить несовместную систему MathCAD выдаёт сообщение об ошибке с предложением поменять начальные значения. Вычислительный блок с функцией Find применим и для решения одного уравнения с одним неизвестным, воспринимаемого как система, состоящая из одного уравнения. Математическая статистика MathCAD предоставляет широкие возможности для работы со статистическими рядами, полученными в ходе эксперимента, либо в результате генерации случайных чисел. Встроенные функции обеспечивают работу со всеми основными типами распределений. Так, например, чтобы воспользоваться функцией плотности вероятности нормально распределённой величины необходимо набрать на клавиатуре dnorm(x,M,s), где x – аргумент функции, M – математическое ожидание, s – среднеквадратическое отклонение. Эту же функцию можно вызвать через главное меню кнопкой «Вставить». В появившемся шаблоне необходимо заполнить три место заполнителя (x,M,s). Для плотностей других распределений в имени функции после первой буквы d необходимо поставить соответствующее буквосочетание, например: - dF(x,k,n) – распределение Фишера, где k, n – степени свободы; - dexp(x,a) – экспоненциальное распределение, где a – показатель экспоненты; - dunif(x,a,b) – равномерное распределение, где a < b – границы интервала; - dt(x,k) – распределение Стьюдента, где k – число степеней свободы. Для обработки статистических рядов имеются встроенные функции, вызываемые как набором на клавиатуре, так и через главное меню: - mean(X) – определение выборочного среднего значения (оценки) случайной величины X; - var(X) – определение выборочной дисперсии (оценки) случайной величины X; - median(X) – определение выборочной медианы (значения функции X, делящего гистограмму плотности вероятностей пополам); - min(X), Max(X) – определение минимального и максимального значения выборки (статистического ряда); - mode(X) – определение наиболее часто встречающегося значения выборки; - corr(X,Y) – определение коэффициента корреляции двух выборок; - ceil(X) – определение наименьшего целого, не меньшего X; - floor(X) – определение наибольшего целого, меньшего или равного X; - gmean(X) – определение геометрического среднего значения выборки. Первоначальную оценку закона распределения случайной величины позволяет сделать анализ гистограммы – графика, аппроксимирующего плотность распределения по случайным данным. Для его построения область значений случайной величины разбивается на некоторое число сегментов (bin), после чего учитывается число (процент) попаданий данных в каждый сегмент. Эти проценты, графически выраженные в виде масштабного столбика над своим сегментом данных, и представляют собой гистограмму случайной величины. Для построения гистограмм предназначена встроенная функция hist(int,X), где X – вектор случайных данных, int – вектор, задающий сегменты построения гистограммы в порядке возрастания и зависящий от их количества bin. Гистограмма строится как двумерный график; в диалоговом окне «Форматирование» необходимо задать вид графика: столбцы (bar) или гистограмма (solidbar). Для анализа на этом же графике можно построить кривую плотности распределения предполагаемого закона, которому подчиняется случайная величина. Функция hist выдаёт вектор, состоящий из значений, каждое из которых равно числу попаданий случайной величины в соответствующий сегмент гистограммы. Поэтому следует обратить внимание на нормировку гистограммы. Так как интеграл от функции плотности вероятностей по всей области возможных значений равен единице, то и сумма площадей всех столбцов гистограммы должна равняться единице. Только в этом случае можно сравнивать аппроксимацию гистограммой с кривой предполагаемой плотности распределения. Функция hist привязывает каждый столбец гистограммы к левой границе сегмента. Привязать столбцы к середине сегмента перед построением графика можно переопределением вектора int. В заключение небольшое замечание относительно тригонометрических функций в MathCAD. В полном объёме представлены как прямые, так и обратные тригонометрические функции. Имеется даже дополнительная функция angle(x,y), определяющая угол между осью 0X и направлением на точку с координатами (x, y), которая может быть полезна в некоторых расчётах. Но следует помнить, что аргументы прямых тригонометрических функций и результаты обратных тригонометрических преобразований выражаются в радианах.
2. Задания для самостоятельной работы Занятие 1 Занятие 2 Построение и оформление графиков Средствами MathCAD определить выражения и функции, построить графики, оформить отчетный материал. _________________________________________________________________
Графики функций: 1. Построить график функции 2. Построить кривую канонического эллипса с полуосями, равными 2 и 4 соответственно вдоль осей x и y. 3. Построить график функции 4. Закон Планка для излучения абсолютно чёрного тела:
Задавшись температурой фона 5. Обработать и представить изображение, полученное в п. 4, с помощью графического редактора. 6. Разместить на одном изображении графики функции 7. Для статистически независимых случайных величин X и Y построить график совместной плотности распределения:
8. Отформатировать полученный материал в качестве отчётного с точки зрения размеров, шрифта, размещения и полноты представления. Преподаватель ________ Суворов С.В.
Занятие 3 Работа с массивами Средствами MathCAD выполнить следующие задания и оформить отчетный материал. _________________________________________________________________
Создание матриц и векторов: 1. Создать матрицу А вида:
2. Сложить матрицу А с числом 3. Создать вектор X длиной
4. Транспонировать X и вывести на лист вектор Y=XТ. 5. Вывести на лист значения элементов Y3 и Y10. 6. Вычислить выборочное среднее значениеY по формуле 7. Вычислить выборочную дисперсию Y по формуле 8. Вычислить
где 9. Построить графики для математического ожидания и дисперсии. 10. Создать внешний файл с вектором-столбцом 11. Транспонировать перенесённый из файла вектор и отобразить его на листе в виде таблицы. 12. Создать внешний файл с матрицей размерностью 3´2 с произвольно заданными элементами и перенести её в MathCAD. 13. Создать заготовку для вектора-столбца 14. Заменить нули произвольными значениями.
Занятие 4 Занятие 5 Занятие 6 Задание 7 Решение уравнений Средствами MathCAD выполнить следующие задания и оформить отчетный материал. _________________________________________________________________
1. Задано уравнение: 2. Задано уравнение: 3. Задан полином: 4. Решить уравнение 5. Определить верхнюю границу спектрального диапазона излучения серого тела ( 6. Заданы две функции: 7. Определить значения переменной g, при которых две заданные функции
Задание 8 Математическая статистика Средствами MathCAD выполнить следующие задания и оформить отчетный материал. _________________________________________________________________
1. Создать два вектора, образованные временной выборкой из двух независимых непрерывных случайных величин, распределённых нормально, в соответствии с таблицей:
2. Найти оценки выборочных средних значений и дисперсии случайных величин X и Y (см. Занятие 3), используя 3 способа: по окончании выборки, рекуррентно, средствами MathCAD. 3. Образовать и визуализировать функцию 4. Показать, что 5. Найти максимальное и минимальное значения случайной величины Z. 6. Найти средствами MathCAD коэффициент корреляции между случайными величинами X и Y, Y и Z. 7. Проверить необходимое условие независимости случайных величин X и Y и, наоборот, зависимости случайных величин Y и Z расчётом по формулам (коэффициент линейной корреляции случайных величин X и Y: 8. Построить гистограмму для случайной величины X. На этом же графике разместить изображение функции плотности вероятности X, построенную по вычисленным в п.2 оценкам среднего значения и дисперсии. Проанализировать результат. 9. Найти средствами MathCAD наименьшее и наибольшее целые значения случайной величины Y. 10. Двумя способами найти угол g (в градусах) между осью 0X и направлением на точку с координатами ( 11. Найти геометрические средние значения случайных величин X, Y, Z. Сделать выводы.
3. Вопросы для подготовки к зачёту 1. Каковы положительные стороны MathCAD? 2. Интерфейс MathCAD. 3. Каким не может быть имя выражения? 4. Особенности цепких операторов. 5. Встроенные функции. 6. Порядок использования функций пользователя. 7. Особенности дискретной переменной. 8. Порядок задания дискретной переменной. 9. В чём отличия порядков задания дискретной переменной? 10. Формат числа и его изменение. 11. Числовые константы. 12. Особенности редактирования объектов. 13. Назначение клавиши пробела. 14. Перемещение, удаление и копирование объектов. 15. Порядок ввода операторов в MathCAD. 16. Что означает окрашивание в красный цвет какой-либо позиции выражения? 17. Порядок ввода текста. 18. Математическая и текстовые области MathCAD. 19. Изменение стиля текста. 20. Как создать графическую область? 21. Порядок действий при создании двумерного графика. 22.Форматирование графиков. 23. Особенности графика двух и более функций. 24. Изменение размера и перемещение графика. 25. Параметрический график. 26. Что можно изменять при форматировании графика? 27. Начальные и пользовательские пределы изменений аргумента на графике. 28. Каково предельное число отображаемых на графике функций? 29. Создание трёхмерного графика. 30. Особенности имени функции при построении трёхмерного графика. 31. Имеете ли опыт использования MathCAD и какой? 32. Какова разница в графиках функции и построенного по дискретным значениям аналогичного выражения? 33. Особенности построения нескольких графиков в пределах одного изображения. 34. Раскройте понятие «массив» применительно к MathCAD. 35. Обращение с массивами. 36. Способы создания массивов. 37. Встроенная переменная ORIGIN. 38. Операция транспонирования при обработке длинной выборки. 39. Применение четырех арифметических операций к массивам. 40. Расшифруйте понятие рекуррентного алгоритма вычислений. 41. Считывание данных из файла в MathCAD. 42. Как придать выведенному на лист массиву желаемый вид? 43. Перенос данных из MathCAD в файл. 44. Особенности матричных операторов и функций при работе со столбцами и строками. 45. Особенности дискретной переменной при работе с массивами. 46. Как решается в MathCAD задача многократных вычислений? 47. Как выглядит в MathCAD выражение-программа? 48. Как создать программу в MathCAD? 49. Порядок ввода программных операторов. 50. Действие кнопки Add Line панели «Программирование». 51. Локальный оператор присваивания. 52. Обособленность программного модуля в MathCAD. 53. Действие условного оператора if. 54. Какова связь между операторами if и otherwise? 55. Что может являться условием, истинность которого проверяется условным оператором if? 56. Как опознать программный модуль в MathCAD? 57. Порядок добавления строк в программе MathCAD. 58. Варианты организации множественных вычислений в MathCAD. 59. Чем похожи и в чём разница между операторами for и while? 60. Как прервать бесконечно длящийся цикл? 61. Порядок создания программного модуля с оператором цикла. 62. Оператор цикла while. 63. Оператор цикла for. 64. Ввод комментария в программу. 65. Досрочное завершение цикла. 66. Символьные вычисления. 67. Варианты символьных вычислений в MathCAD. 68. Какова разница между двумя вариантами символьных вычислений в MathCAD? 69. Порядок выполнения символьных вычислений. 70. Панель символьных вычислений. 71. Дифференцирование в MathCAD. 72. Интегрирование в MathCAD. 73. Влияние исходной функции при интегрировании. 74. Порядок проведения операции дифференцирования. 75. Порядок проведения операции интегрирования. 76. Как реагирует MathCAD на отсутствие аналитического решения? 77. Каков порядок графического решения уравнения? 78. Возможности решения одного уравнения в MathCAD. 79. От чего зависит точность решения уравнений? 80. Какова роль начального значения предполагаемого решения? 81. Порядок решения системы уравнений. 82. Нахождение корней полинома. 83. Константы TOL и CTOL. 84. Ограничения встроенной функции root при решении уравнений. 85. Каким образом записывается система уравнений при решении средствами MathCAD? 86. Что означает выдача сообщения об ошибке при попытке решить уравнение или систему уравнений? 87. Возможности MathCAD по решению одного уравнения. 88. Каковы возможности MathCAD по обработке статистических рядов? 89. Порядок построения гистограммы. 90. Объясните действия встроенной функции hist. 91. Особенность тригонометрических функций в MathCAD. 92. Как оценить закон распределения случайной величины средствами MathCAD? 93. Нормирование гистограммы. 94. Встроенная функция dnorm. 95. Ваши впечатления от знакомства с MathCAD.
Учебная литература: 1. Суворов С.В. Математический редактор MathCAD. Основы работы: учебно-методическое пособие. – М.: Издательство МГТУ им. Н.Э. Баумана, 2019. – 37 с. 1. Макаров Е.Г. Инженерные расчёты в MathCAD: Учебный курс. – СПб.: Питер, 2003. – 448 с. 2. Половко А.М., Ганичев И.В. MathCAD для студента. – СПб.: БХВ-Петербург, 2006. – 336 с. 3. Макаров Е.Г. Инженерные расчёты в MathCAD 15: Учебный курс. – СПб.: Питер, 2011. – 400 с. 4. http://www.mathcad.com – начальная страница фирмы Mathsoft.
Методические указания по проведению учебно-технологической практики (УТП) в группах первого курса
Математический пакет MathCAD
Москва, 2016 Цель преподавания УТП – содействие формированию профессиональных компетенций при проведении инженерных расчетов с использованием математического пакета MathCAD в общепрофессиональной, производственно-технологической и научно-исследовательской деятельности. Задачами преподавания УТП являются освоение: - основных возможностей пакета; - первичных навыков построения и вычисления выражений, редактирования объектов, работы с дискретными переменными, таблицами, графиками; - первичных навыков программирования; - первичных навыков символьных вычислений, дифференцирования и интегрирования выражений; - правил техники безопасности и внутреннего распорядка. Прохождение распределенной практики (практикума) заключается в проведении аудиторных занятий с предоставлением каждому студенту индивидуального рабочего места, оборудованного персональным компьютером с программным обеспечением, и самостоятельной работы студентов над учебным пособием и указанной литературой по дисциплине. Во время аудиторных занятий проводятся индивидуальная и коллективная консультации студентов с преподавателем. Основные сведения о MathCAD MathCAD – инструмент для работы инженеров, мощный калькулятор, имеющий следующие преимущества: - запись математических выражений в обычном инженерном виде; - простота использования; - возможность создания качественных технических отчетов с таблицами, графиками, текстом; - дискретная переменная, позволяющая вычислять одновременно функцию для целого ряда аргументов. Рабочее окно MathCAD выглядит аналогично другим Windows приложениям. Главное меню – верхняя строка рабочего окна. В нём можно выполнить любые действия. Панели инструментов – для быстрого выполнения часто применяемых команд: - стандарт
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 98; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.170.65 (0.012 с.) |

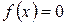 MathCAD предоставляет встроенную функцию root, которая может быть использована в двух вариантах. В первом из них искомому решению уравнения присваивается значение
MathCAD предоставляет встроенную функцию root, которая может быть использована в двух вариантах. В первом из них искомому решению уравнения присваивается значение 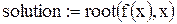 . Перед этим необходимо задать функцию
. Перед этим необходимо задать функцию 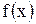 и присвоить x некоторое значение, вблизи которого будет проводиться поиск решения. Во втором варианте искомому решению присваивается значение
и присвоить x некоторое значение, вблизи которого будет проводиться поиск решения. Во втором варианте искомому решению присваивается значение 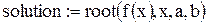 , где (a,b) – интервал, внутри которого заведомо находится искомое решение. После этого его нужно вывести на экран (
, где (a,b) – интервал, внутри которого заведомо находится искомое решение. После этого его нужно вывести на экран (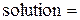 ). Решение ищется численными методами, а его поиск начинается с выбранного значения или интервала с последующим приближением к истинному значению. Функцию
). Решение ищется численными методами, а его поиск начинается с выбранного значения или интервала с последующим приближением к истинному значению. Функцию 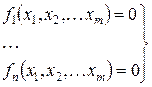
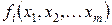 – скалярная функция скалярных переменных. Для решения такой системы необходимо обратиться к специальному вычислительному блоку, состоящему из трёх частей:
– скалярная функция скалярных переменных. Для решения такой системы необходимо обратиться к специальному вычислительному блоку, состоящему из трёх частей: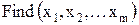 , решающей систему.
, решающей систему.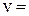 ) выводит на экран решение системы. В выведенном на экран векторе v первый элемент представляет собой решение системы по первому аргументу, второй элемент – по второму аргументу и т.д. Общее число элементов вектора v равно числу переменных функции Find.
) выводит на экран решение системы. В выведенном на экран векторе v первый элемент представляет собой решение системы по первому аргументу, второй элемент – по второму аргументу и т.д. Общее число элементов вектора v равно числу переменных функции Find.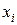 должны быть присвоены начальные значения;
должны быть присвоены начальные значения;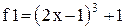 . Оформить в виде, позволяющем рассмотреть точку перегиба.
. Оформить в виде, позволяющем рассмотреть точку перегиба.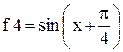 в укрупнённом масштабе.
в укрупнённом масштабе.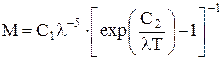 , где
, где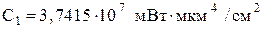 ,
, 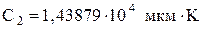 .
.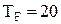 °C и нагретого тела
°C и нагретого тела 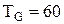 °C, показать графически разницу в их излучательной способности. Прокомментировать полученный результат.
°C, показать графически разницу в их излучательной способности. Прокомментировать полученный результат.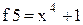 и выражения
и выражения 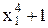 при изменении
при изменении 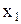 от –1,5 до +1,5 с шагом 0,5. Прокомментировать разницу в графиках.
от –1,5 до +1,5 с шагом 0,5. Прокомментировать разницу в графиках.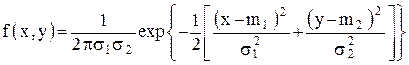 .
.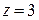 .
.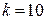 и с начальным индексом единица:
и с начальным индексом единица: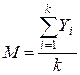 .
.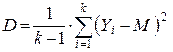 .
.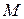 и
и 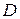 по рекуррентному алгоритму по формулам:
по рекуррентному алгоритму по формулам:
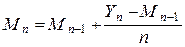 ;
;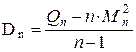 ,
,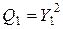 ;
; 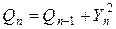 . Для рекуррентного алгоритма математическому ожиданию
. Для рекуррентного алгоритма математическому ожиданию  и
и  .
.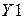 с десятью произвольно заданными элементами и перенести его в MathCAD.
с десятью произвольно заданными элементами и перенести его в MathCAD. с нулевыми значениями шести элементов.
с нулевыми значениями шести элементов.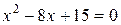 . Необходимо: а) решить уравнение графически; б) решить уравнение разложением на множители; в) решить уравнение с помощью встроенной функции root; г) решить уравнение с помощью встроенной функции polyroots.
. Необходимо: а) решить уравнение графически; б) решить уравнение разложением на множители; в) решить уравнение с помощью встроенной функции root; г) решить уравнение с помощью встроенной функции polyroots.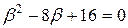 . Необходимо: а) решить уравнение графически; б) решить уравнение разложением на множители; в) решить уравнение с помощью встроенной функции root для разных значений константы (TOL), определяющей точность численных методов: заданной по умолчанию TOL=0,001 и заданной пользователем TOL=0,000001; г) решить уравнение с помощью встроенной функции polyroots. По окончании вернуть константе значение, принятое по умолчанию.
. Необходимо: а) решить уравнение графически; б) решить уравнение разложением на множители; в) решить уравнение с помощью встроенной функции root для разных значений константы (TOL), определяющей точность численных методов: заданной по умолчанию TOL=0,001 и заданной пользователем TOL=0,000001; г) решить уравнение с помощью встроенной функции polyroots. По окончании вернуть константе значение, принятое по умолчанию. . Необходимо: а) найти корни полинома графически; б) найти корни полинома разложением на множители; в) найти корни полинома с помощью встроенной функции polyroots.
. Необходимо: а) найти корни полинома графически; б) найти корни полинома разложением на множители; в) найти корни полинома с помощью встроенной функции polyroots.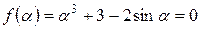 , определив функцию
, определив функцию 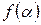 как вне функции root, так и внутри неё. Сравнить с графическим решением.
как вне функции root, так и внутри неё. Сравнить с графическим решением. ) при нижней границе 6 мкм, чтобы оно обеспечило мощность излучения 20 Вт, если оно имеет излучающую поверхность в виде круга диаметром 20 см, а собственная температура равна 80°С и 150°С.
) при нижней границе 6 мкм, чтобы оно обеспечило мощность излучения 20 Вт, если оно имеет излучающую поверхность в виде круга диаметром 20 см, а собственная температура равна 80°С и 150°С.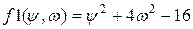 и
и 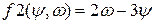 . Систему уравнений
. Систему уравнений 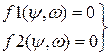 решить тремя способами: а) графически; б) алгебраически; в) с помощью вычислительного блока MathCAD. Проверить правильность решения.
решить тремя способами: а) графически; б) алгебраически; в) с помощью вычислительного блока MathCAD. Проверить правильность решения.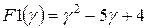 и
и 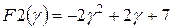 имеют одинаковые значения. Проверить полученный результат.
имеют одинаковые значения. Проверить полученный результат.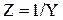 . Найти оценки её выборочных средних значений и дисперсии.
. Найти оценки её выборочных средних значений и дисперсии.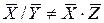 . В некоторых измерительных приборах информативной величиной является небольшая разность двух случайных величин, полученная на фоне одной из них. Применительно к рассматриваемым случайным величинам результат измерения можно получить, пользуясь двумя выборками из трёх
. В некоторых измерительных приборах информативной величиной является небольшая разность двух случайных величин, полученная на фоне одной из них. Применительно к рассматриваемым случайным величинам результат измерения можно получить, пользуясь двумя выборками из трёх 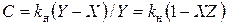 , где
, где 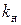 – нормирующий коэффициент. Показать, что имеет место неравенство
– нормирующий коэффициент. Показать, что имеет место неравенство 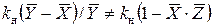 . Убедитесь, что
. Убедитесь, что 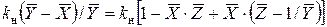 . Принять
. Принять 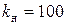 .
.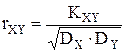 , где
, где 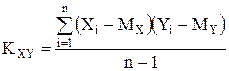 , n – длина выборок).
, n – длина выборок).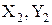 ), а также sin(g).
), а также sin(g).


