Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Молекулы взаимодействуют между собой.Содержание книги Поиск на нашем сайте
Первое положение МКТ подтверждается тем, что в настоящее время получены фотографии молекул. Второе положение можно подтвердить диффузией и броуновским движением. Диффузия – явление перемешивания веществ. Броуновское движение – движение мельчайших частиц, находящихся во взвешенном состоянии под действием молекул окружающей среды (цветочная пыльца, раствор туши, частицы пыли в воздухе и т. д.). Интенсивность броуновского движения пропорциональна температуре окружающей среды.
Идеальный газ и его параметры В МКТ пользуются понятием идеальный газ, который удовлетворяет следующим условиям: 1. Объем занимаемый молекулами газа мал по сравнению с объемом сосуда. 2. Молекулы газа не взаимодействуют друг с другом. 3. Столкновения друг с другом и со стенками сосуда абсолютно упругие. Идеальный газ характеризуется следующим параметрами: V – объем. Газ полностью занимает объем сосуда, в котором находится; P – давление. Обусловлено ударами молекул о стенки сосуда;
t – температура – степень нагретости тела. Определяется кинетической энергией поступательного движения молекул.
23. 4.Экспериментальные газовые законы Рассмотрим законы, выведенные экспериментально и устанавливающие зависимость между р,V и T. Закон Бойля-Мариотта Закон Бойля-Мариотта устанавливает зависимость между давлением и объемом при постоянной температуре. Запишем основное уравнение МКТ для двух состояний газа: Так, как правые части уравнений (8.13) и (8.14) равны, приравняем левые:
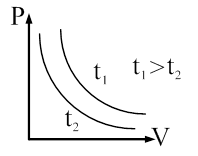
Закон Бойля-Мариотта: произведение давления на объем данной массы газа есть величина постоянная при неизменной температуре. Процесс, протекающий при T = const называется изотермическим и изображается изотермой (рис. 58):
Рис. 58.
Закон Гей-Люссака Закон Гей-Люссака устанавливает зависимость между объемом и температурой при постоянном давлении. Запишем основное уравнение МКТ для двух состояний газа:
Разделим почленно уравнение (8.15) на (8.16) и получим:
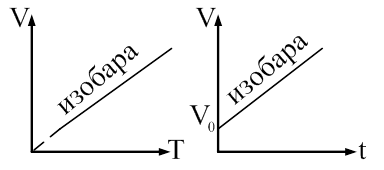
Закон Гей-Люссака: объем данной массы газа прямо пропорционален абсолютной температуре при постоянном давлении. Закон Гей-Люссака через температуру по шкале Цельсия перепишется в виде: где α = 1/273 К -1 – коэффициент объемного расширения; V0– объем при 0 0С; t– температура. Процесс, протекающий при постоянном давлении называется изобарическими изображается изобарой (рис. 59).
Рис. 59 Закон Шарля Закон Шарля устанавливает зависимость между давлением ри температурой Т при постоянном объеме. Запишем основное уравнение МКТ для двух состояний газа: Разделим почленно (8.18) на (8.19) и получим:
Закон Шарля: давление данной массы газа пропорционально абсолютной температуре при постоянном объеме. Через температуру по шкале Цельсия закон Шарля запишется где α = 1/273 К-1, P0 – давление при 00С. Процесс в газах, протекающий при постоянном объеме называется изохорным и изображается изохорой (рис. 60).
Рис. 60
Адиабатический процесс Адиабатным, называется процесс, протекающий без теплообмена с окружающей средой (рис. 61).
Рис. 61 Абсолютный нуль Рассмотрим график изохорического процесса в координатных осях P-t (рис. 62).
Рис. 62.
При понижении температуры давление, производимое газом, будет уменьшаться. Запишем закон Шарля:
Найдем температуру, при которой давление, производимое газом
Абсолютный нуль - это температура, при которой прекращается поступательное движение молекул и давление, производимое газом становится равным нулю.
24. 3. Основное уравнение МКТ Основное уравнение молекулярно-кинетической теории идеального газа устанавливает зависимость между давлением (p); объемом (V) и кинетической энергией поступательного движения его молекул. Для вывода формулы рассмотрим одноатомный идеальный газ, находящийся в цилиндрическом сосуде с площадью основания ∆ S и длиной l (рис. 56).
Рис. 56.
Молекулы движутся хаотически и беспорядочно, их количество N. Определим давление, оказываемое газом на площадку
где
где Импульс одной молекулы равен:
Так как после удара о стенки сосуда направление скорости изменится на Общее количество молекул в сосуде будет равно:
где
Рассчитаем импульс ∆ p, сообщенный площадке С учетом уравнения (8.3) уравнение (8.5) примет вид:
Подставим значение ∆ p из уравнения (8.6) в (8.2) и выразим силу Подставим правую часть уравнения (8.7) в уравнение (8.1):
Молекулы в сосуде движутся со скоростями
C введением основное уравнение МКТ идеального газа. Умножив и разделив правую часть уравнения (8.9) на 2, получим другой вид данного уравнения:
где По закону Больцмана Подставив значение Т. к. концентрация газа (8.12) 25.. Уравнение Менделеева-Клапейрона.
|
||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 91; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.38.184 (0.008 с.) |

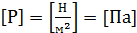 .
.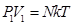 (8.13)
(8.13)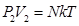 (8.14)
(8.14)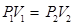 или
или 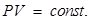
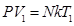 (8.15)
(8.15)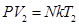 . (8.16)
. (8.16)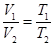
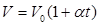 ,
,
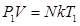 (8.18)
(8.18)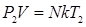 (8.19)
(8.19)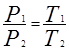 (8.20)
(8.20) , (8.21)
, (8.21) 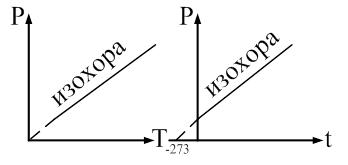
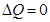 . Графически адиабатический процесс представляется адиабатой. Рассмотрим этот процесс в координатных осях
. Графически адиабатический процесс представляется адиабатой. Рассмотрим этот процесс в координатных осях 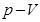
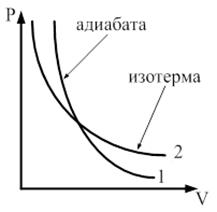 Адиабата в осях
Адиабата в осях  представляет собой гиперболу, которая более крута, чем изотерма, т. к. при адиабатическом процессе 1-2 возрастает давление и изменяется температура.
представляет собой гиперболу, которая более крута, чем изотерма, т. к. при адиабатическом процессе 1-2 возрастает давление и изменяется температура.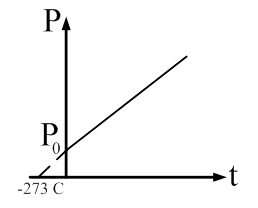
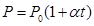 (8.22)
(8.22)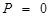
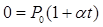
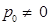 ,следовательно
,следовательно 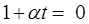 ,
, 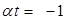 →
→ 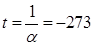 0C.
0C.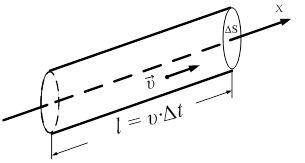
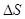 .
.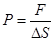 (8.1)
(8.1)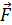 – сила, которая может быть выражена по второму закону Ньютона через импульс тела:
– сила, которая может быть выражена по второму закону Ньютона через импульс тела: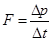 (8.2)
(8.2)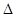 p – импульс.
p – импульс.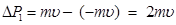 . (8.3)
. (8.3)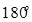
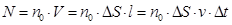 . (8.4)
. (8.4)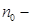 концентрация.
концентрация.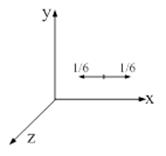 Молекулы движутся к площадке под разными углами. Для упрощения расчетов предположим, что молекулы движутся вдоль трех взаимно перпендикулярных направлений, 1/3 молекул вдоль каждого направления, причем половина молекул (1/6) движется в одну сторону, половина в противоположную (рис. 57). С учетом этого до площадки ∆ S дойдет 1/6 от (Рис. 57) N – общего числа молекул.
Молекулы движутся к площадке под разными углами. Для упрощения расчетов предположим, что молекулы движутся вдоль трех взаимно перпендикулярных направлений, 1/3 молекул вдоль каждого направления, причем половина молекул (1/6) движется в одну сторону, половина в противоположную (рис. 57). С учетом этого до площадки ∆ S дойдет 1/6 от (Рис. 57) N – общего числа молекул.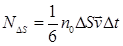 (8.5)
(8.5)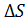 этими молекулами.
этими молекулами.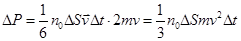 (8.6)
(8.6)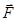 :
: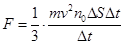 (8.7)
(8.7)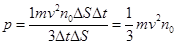 (8.8)
(8.8)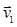 ;
; 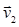 ; …
; … 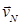 в этом случае рассматривают среднюю квадратичную скорость
в этом случае рассматривают среднюю квадратичную скорость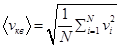
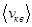 уравнение (8.8) перепишется в виде:
уравнение (8.8) перепишется в виде: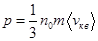 - (8.9)
- (8.9)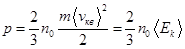 (8.10)
(8.10)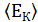 – средняя кинетическая энергия поступательного движения молекул.
– средняя кинетическая энергия поступательного движения молекул.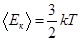 , где k–постоянная Больцмана, Т – абсолютная температура.
, где k–постоянная Больцмана, Т – абсолютная температура.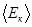 в (8.10) получим еще два вида основного уравнения МКТ идеального газа:
в (8.10) получим еще два вида основного уравнения МКТ идеального газа: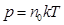 (8.11)
(8.11)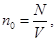 то уравнение (8.11) перепишется в виде:
то уравнение (8.11) перепишется в виде: