
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кривая безразличия и ее свойства.Содержание книги
Поиск на нашем сайте
Предельная норма замещения
Для визуального представления о порядковой полезности используются кривые безразличия и карта кривых безразличия, которые описывают предпочтения индивидуального потребителя. Этот инструмент в экономике впервые применен английским экономистом Ф. Эджуортом в 1881 г. С 1935 г. после опубликования работ Хикса и Алена кривые безразличия стали широко применяться в анализе потребительского выбора.
Рис. 1.2. Кривая безразличия Кривая безразличия (линия равной полезности) (рис. 1.2)представляет собой геометрическое место точек[7], каждая из которых описывает потребительский набор (например А(х1,у1), или В(х2,у2)), имеющий одинаковую полезность для данного потребителя. Бесконечное множество кривых безразличия, соответствующих всем возможным уровням полезности для данного потребителя образует карту кривых безразличия (рис. 1.3).
Рис. 1.3. Карта кривых безразличия
Рассмотрим свойства кривых безразличия. 1. Кривые безразличия имеют отрицательный наклон. Это свойство обусловлено требованием субституции, которое заключается в следующем: потребительские наборы будут сохранять одинаковую полезность (а потребитель, соответственно будет находиться на одной кривой безразличия), в том случае если увеличение одного блага в наборе, сопровождающееся приростом полезности на некоторую величину, будет компенсироваться уменьшением другого блага, что влечет за собой снижение полезности. Таким образом, линия равной полезности в общем случае приобретает отрицательный наклон. 2. Две кривые безразличия не могут пересекаться. Доказательство этого свойства проведем методом «от противного». Представим, что две кривые безразличия (U1 и U2), описывающие предпочтения одного и того же потребителя, пересеклись в некоторой точке А (рис. 1.4). В этом случае один и тот же потребительский набор А(хА,уА) соответствует двум разным (!) уровням полезности. Чего быть не может. Свойство доказано.
Рис. 1.4. Кривые безразличия не могут пересекаться
3. Кривая безразличия, лежащая выше и правее другой кривой, представляет собой более предпочтительные для данного потребителя наборы товаров. Рассмотрим на рис. 1.5 кривые безразличия U1 и U2. Набор В включает в себя такое же количество блага «у», что и набор А, однако количество блага «х» в этом наборе больше. Тогда, в соответствии с аксиомой ненасыщения (аксиомой 3), набор «В» является более предпочтительным, т. е. приносит больше полезности, чем набор «А».
Рис. 1.5. Кривые безразличия
4. Кривые безразличия выпуклы по отношению к началу координат. Это свойство, в отличие от предыдущих, не может быть выведено непосредственно из аксиом потребительского выбора. Для обоснования этого свойства кривых безразличия необходимо ввести в рассмотрение ключевое операционное понятие порядковой теории полезности — предельную норму замещения (MRSxy; marginal rate of substitution — англ.). Предельной нормой замещения благом Х блага У (MRSxy) называют количество блага У, которое должно быть изъято из потребительского набора «в обмен» на увеличение количества блага Х на единицу, с тем, чтобы уровень полезности потребительского набора остался для потребителя неизменным:
Знак минус, вводимый перед правой частью (5) делает значение нормы замещения положительной (помним, что отрицательный наклон кривой безразличия по определению обусловливает отрицательное значение отношения Пусть потребитель безразличен между наборами А и В (рис. 1.6).
Рис. 1.6. Предельная норма замещения
Норма замещения при движении вдоль кривой безразличия уменьшается. Этот вывод является следствием закона убывания предельной полезности: с увеличением количества блага Х и, соответственно, уменьшением количества блага У потребитель все больше ценит ставшее относительно более дефицитным благо У и, следовательно, готов отдать все меньшее количество единиц этого блага в обмен на каждую следующую единицу блага Х. Если представить приращение блага Х в виде бесконечно малой величины, то предельную норму замещения можно описать следующим выражением:
Очевидно, что предельная норма замещения в этом случае равна угловому коэффициенту наклона касательной к кривой безразличия в точке А. Таким образом, предположение об уменьшении предельной нормы замещения при движении вдоль кривой безразличия, обусловливающее ее выпуклость, доказано. Следует отметить, что чем более взаимозаменяемы товары Х и У, тем менее выпуклы кривые безразличия.
Итак, карта кривых безразличия — множество кривых безразличия — дает исчерпывающую информацию о системе предпочтений экономического индивидуума. Однако, для того, чтобы прогнозировать рациональный потребительский выбор этой информации недостаточно. Решение данной задачи требует введения еще одного специального инструмента, предназначенного для описания множества допустимых возможностей потребителя — бюджетной линии. Бюджетное ограничение потребителя.
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.102.88 (0.01 с.) |


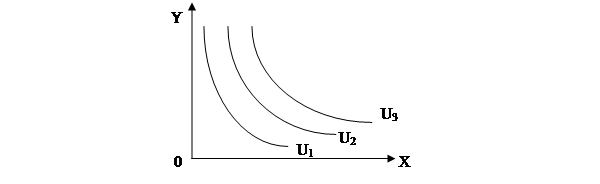
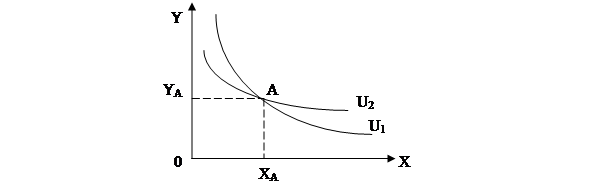

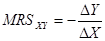 , при
, при 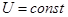 . (5)
. (5)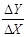 ).
).
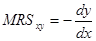 . (6)
. (6)


