Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка качества переходного процессаСодержание книги
Поиск на нашем сайте
По расположению корней характеристического уравнения
Как известно, вид корней характеристического уравнения определяет характер переходного процесса. Следовательно, расположение корней позволяет оценить качество переходного процесса. Впервые оценка качества по расположению корней была предложена Вишнеградским И.А. в 1876 году при исследовании САУ 3-го порядка. Диаграмма Вишнеградского Рассмотрим характеристическое уравнение 3-го порядка:
Получим: По критерию Гурвица граница устойчивости будет иметь уравнение: Далее разбиваем область устойчивости на три подобласти:
I область: ближайший к началу координат корень – комплексный. Переходный процесс будет колебательным.
II область: экспоненциально-колебательный переходный процесс.
III область: апериодический переходный процесс.
IV область: переходный процесс расходится. Далее диаграмма Вишнеградского была доработана и вся область разбита вспомогательными линиями, позволяющими оценить быстродействие, запас устойчивости и колебательности. Особенности нелинейных САУ 1. Не действует принцип суперпозиции. В линейных САУ принцип суперпозиции позволял вычислять реакцию системы на сумму нескольких воздействий как сумму реакции на некоторое воздействие. В линейных САУ, при увеличении входного сигнала выходной сигнал увеличивался пропорционально, то есть характер переходных процессов (форма графика и устойчивость) не изменяются. В нелинейной САУ реакция на сумму воздействий не равна сумме реакций на отдельное воздействие:
2. В нелинейных САУ характер движения зависит и от формы входного сигнала и от его амплитуды.
САУ устойчива в “малом” и неустойчива в “большом”
3. Для нелинейных САУ характерным является режим незатухающих колебаний, возникающих из самого принципа работы. В этом случае мы не можем получить какого-то постоянного значения выходной величины. Автоколебания могут быть одночастотными и многочастотными. На одних частотах колебания будут устойчивыми, на других – нет.
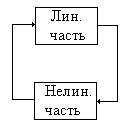
4. В нелинейных САУ при затухании колебаний происходит изменение частоты колебаний. 5. Соединения нелинейных звеньев обладают рядом особенностей: I. Некоммутативность (переставлять нельзя!). II. Не всегда существует обратный оператор (у линейных В результате выделяют два класса нелинейных систем: I класс: удается сгруппировать все линейные звенья в одну группу, нелинейные – в другую.
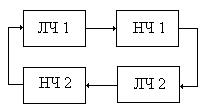
II класс: есть несколько групп линейных и нелинейных звеньев и они чередуются между собой.
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.241.87 (0.009 с.) |

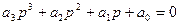 разделим на а0
разделим на а0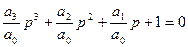 введем новую переменную
введем новую переменную 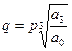
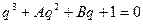 , где
, где 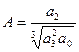
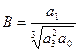
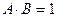
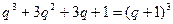 - в точке (3;3) имеем корень тройной кратности
- в точке (3;3) имеем корень тройной кратности 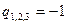
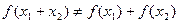
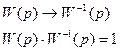 )
)