
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подходящие дроби, их свойства и применение
В предыдущем параграфе мы установили, что всякую обыкновенную дробь можно представить в виде цепной дроби. Поставим обратную задачу: восстановить по цепной дроби исходную обыкновенную дробь. Рассмотрим цепную дробь
Чтобы найти обыкновенную дробь можно выполнить вычисления, “поднимаясь” по цепной дроби снизу вверх:
Другой, более удобный способ вычисления состоит в использовании подходящих дробей. Определение 13.1. Дроби
Теорема 13.1. Подходящие дроби несократимы. Доказательство. Докажем теорему методом математической индукции по числу n –количеству неполных частных, составляющих подходящую дробь. 1) База индукции. Пусть частное 2) Индукционный переход. Предположим, что утверждение теоремы верно для дроби, состоящей из Рассмотрим дробь, состоящую из Запишем дробь Теорема 13.2. (Закон составления подходящих дробей). Пусть Доказательство. Докажем теорему методом математической индукции по числу k –номеру подходящей дроби. 1) База индукции. Пусть 2) Индукционный переход. Пусть (13.1) верно для Заметим, что если представить подходящую дробь в сокращенной записи, то индукционное предположение означает, что утверждение теоремы верно для подходящих дробей с количеством неполных частных, не превосходящем Докажем, что (13.1) верно также для
Поскольку По индукционному предположению
Докажем, что из этого равенства дробей следует равенство их числителей и знаменателей. При представлении числа Таким образом, если Подходящая дробь с номером Тогда подходящая дробь Таким образом мы получили, что в дробях в правой и левой частей равенства (13.2) знаменатели равны, значит равны и числители. Теорема доказана.
Таким образом мы получили, что в дробях в правой и левой частей равенства (13.2) знаменатели равны, значит равны и числители. Теорема доказана.
Итак, мы получили рекуррентное соотношение для вычисления подходящих дробей. Выкладки можно проводить, заполняя таблицу:
Пример. Найти рациональное число, равное цепной дроби Составим таблицу и заполним ее, используя формулы (13.1):
Итак, мы получили, что При помощи закона составления подходящих дробей можно вывести ряд их свойств.
Свойства подходящих дробей
Свойство 1. Доказательство. Докажем свойство методом математической индукции по индексу k. 1) База индукции. Пусть Тогда 2) Индукционный переход. Пусть свойство верно для
Свойство 2. Доказательство. Доказательство свойства непосредственно следует из свойства 1. Свойство 3. С увеличением номера подходящие дроби четного порядка увеличиваются, а нечетного порядка уменьшаются. Доказательство. По закону составления подходящих дробей имеем: Вычислим
По свойству 1 подходящих дробей Если число k – четное, то Свойство 4. Рассмотрим отрезки Доказательство. По свойству 3 выполняются неравенства:
По свойству 2 имеем: Следствие. Представим рациональное число в виде цепной дроби и составим ее подходящие дроби. Тогда данное рациональное число заключено между любыми двумя соседними подходящими дробями. Доказательство следствия вытекает непосредственно из утверждения свойства 4. Свойство 5. Последовательность знаменателей подходящих дробей, начинающаяся с Доказательство. По закону составления подходящих дробей База индукции. Пусть Индукционный переход. Пусть утверждение верно для
Применение подходящих дробей к решению неопределенных уравнений. Свойства подходящих дробей приводят к еще одному способу решения неопределенных уравнений. Рассмотрим этот способ сначала для частного случая неопределенных уравнений, а именно уравнения вида при условии Рассмотрим несократимую дробь Тогда Если число n четное, то представим дробь Рассмотрим теперь общий случай неопределенного уравнения: при условии, что Для решения этого уравнения при помощи подходящих дробей сведем уравнение (13.4) к уравнению типа (13.3) и найдем его частное решение при помощи подходящих дробей. Затем так же, как это было сделано выше (см. § 6) найдем общее решение исходного уравнения (13.4).
Итак, разделим обе части уравнения (13.4) на d, получим уравнение
где Затем рассмотрим вспомогательное уравнение Решим его при помощи подходящих дробей. Пусть числа Общее решение уравнения (13.4) вычисляется по формуле
Примеры. 1) Решить уравнение Как было установлено выше, частным решением данного уравнения являются знаменатель и числитель предпоследней подходящей дроби. Найдем подходящие дроби, для этого составим таблицу:
Выпишем частное решение уравнения: 2) Решить уравнение Поскольку Положим Рассмотрим теперь вспомогательное уравнение: Для его решения рассмотрим дробь Найдем подходящие дроби, для этого составим таблицу:
Выпишем частное решение уравнения (13.9): Упростим полученное решение: Поскольку уравнение (13.7) равносильно уравнению (13.6), полученное решение является также решением исходного уравнения (13.6).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 780; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.193.207 (0.077 с.) |
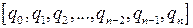
 .
.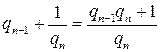 ;
; 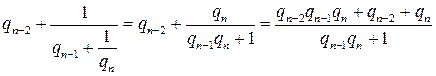 и т. д.
и т. д.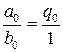 ,
, 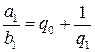 ,
, 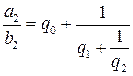 ,…,
,…, 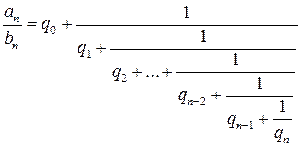 называются подходящими дробями.
называются подходящими дробями. . Дробь, содержащая одно неполное
. Дробь, содержащая одно неполное , очевидно, несократима.
, очевидно, несократима. неполных частных при
неполных частных при 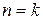 . Докажем, что тогда и дробь, состоящая из
. Докажем, что тогда и дробь, состоящая из 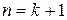 также несократима.
также несократима.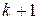 неполного частного:
неполного частного: 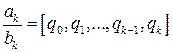 . Эту дробь можно записать в виде:
. Эту дробь можно записать в виде:  , где
, где  . По индукционному предположению дробь
. По индукционному предположению дробь  несократима, так как состоит из
несократима, так как состоит из 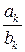 в виде:
в виде: 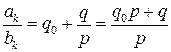 . Докажем, дробь
. Докажем, дробь  и p взаимно просты. Предположим, что последнее утверждение неверно: дробь
и p взаимно просты. Предположим, что последнее утверждение неверно: дробь  . Тогда
. Тогда 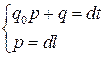 , где
, где  . Из этой системы следует, что
. Из этой системы следует, что  , значит d – общий делитель чисел p и q, причем
, значит d – общий делитель чисел p и q, причем  . Это противоречит тому, что числа p и q взаимно просты. Полученное противоречие означает, что сделанное предположение о том, что дробь
. Это противоречит тому, что числа p и q взаимно просты. Полученное противоречие означает, что сделанное предположение о том, что дробь  – подходящие дроби. Положим
– подходящие дроби. Положим 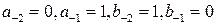 . Тогда
. Тогда 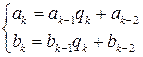 для
для  . (13.1)
. (13.1)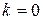 . Тогда
. Тогда 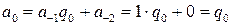 ,
, 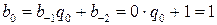 . Подходящая дробь
. Подходящая дробь  , это верно.
, это верно.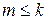 :
: 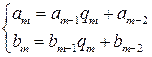 .
.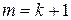 :
: 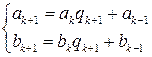 .
.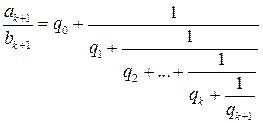 и
и  , при замене в дроби
, при замене в дроби  на
на 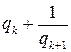 , получим дробь
, получим дробь 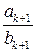 .
. . Заменим
. Заменим 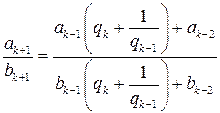 . Преобразуем правую часть этого равенства:
. Преобразуем правую часть этого равенства:
 . Заменяя выражения в скобках в числителе и в знаменателе в последней дроби на
. Заменяя выражения в скобках в числителе и в знаменателе в последней дроби на 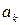 и
и  соответственно, получим равенство
соответственно, получим равенство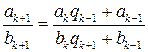 . (13.2)
. (13.2)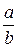 в виде цепной дроби мы использовали алгоритм Евклида, из которого следует, что
в виде цепной дроби мы использовали алгоритм Евклида, из которого следует, что 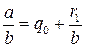 и
и 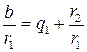 .
.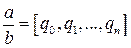 , то, очевидно,
, то, очевидно,  .
.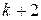 неполных частных:
неполных частных: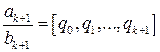 .
.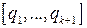 для числа
для числа 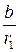 содержит
содержит  .
. . Количество неполных частных в подходящей дроби равно
. Количество неполных частных в подходящей дроби равно  , и отсюда
, и отсюда 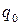

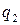
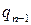
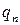


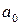


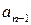

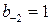
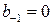
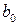
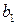
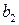

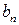
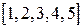 .
.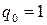
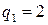
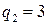
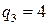
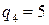

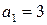
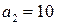
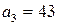
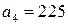
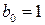
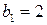
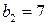

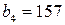
 .
. для
для 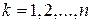 .
. . Вычислим
. Вычислим 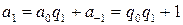 ,
,  .
.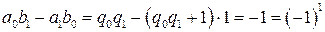 .
. :
:  . Докажем, что оно верно и для
. Докажем, что оно верно и для 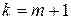 . Действительно,
. Действительно, 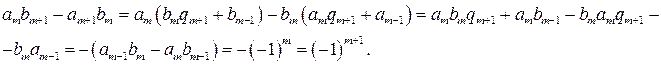
 для
для 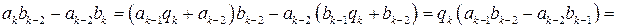
 .
.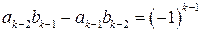 , отсюда следует, что
, отсюда следует, что 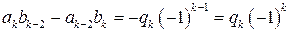 .
. , следовательно
, следовательно 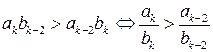 . Если число k – нечетное, то
. Если число k – нечетное, то 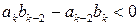 , и тогда
, и тогда  .
. для
для 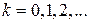 . Тогда
. Тогда  .
.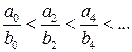 и
и 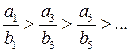 .
.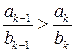 , а для нечетных k – неравенство
, а для нечетных k – неравенство  . Это значит, что все подходящие дроби с четными номерами меньше всех подходящих дробей с нечетными номерами, откуда и следует справедливость доказываемого утверждения.
. Это значит, что все подходящие дроби с четными номерами меньше всех подходящих дробей с нечетными номерами, откуда и следует справедливость доказываемого утверждения.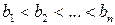 .
.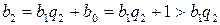 . Поскольку
. Поскольку  ,
, 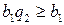 . Следовательно,
. Следовательно, 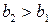 .
.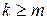 . Это значит, что
. Это значит, что 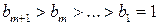 . Докажем, что оно верно и для
. Докажем, что оно верно и для 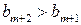 . По закону составления подходящих дробей
. По закону составления подходящих дробей  . А поскольку
. А поскольку  , справедливо
, справедливо  , (13. 3)
, (13. 3) . Как было установлено выше, такое уравнение всегда имеет решение.
. Как было установлено выше, такое уравнение всегда имеет решение.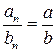 , причем
, причем 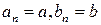 . Рассмотрим сначала случай, когда число n нечетное. По свойству 1 имеем:
. Рассмотрим сначала случай, когда число n нечетное. По свойству 1 имеем: 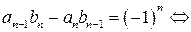

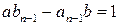 .
.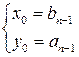 – частное решение уравнения. Общее решение уравнения получим так же, как при решении неопределенных уравнений другими способами:
– частное решение уравнения. Общее решение уравнения получим так же, как при решении неопределенных уравнений другими способами: 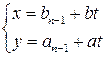 , где
, где  .
.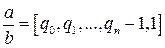 . Тогда последнее “неполное частное”, равное 1, имеет нечетный номер, и уравнение можно решать также, как было рассмотрено выше.
. Тогда последнее “неполное частное”, равное 1, имеет нечетный номер, и уравнение можно решать также, как было рассмотрено выше.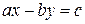 , (13.4)
, (13.4)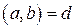 и
и 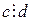 . В этом случае, как было установлено выше, уравнение имеет решение.
. В этом случае, как было установлено выше, уравнение имеет решение. , (13.5)
, (13.5)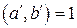 . Уравнение (13.5), очевидно, равносильно уравнению (13.4).
. Уравнение (13.5), очевидно, равносильно уравнению (13.4). .
.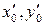 составляют его частное решение. Тогда числа
составляют его частное решение. Тогда числа 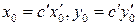 составляют частное решение уравнения (13.5), а значит, и исходного уравнения (13.4).
составляют частное решение уравнения (13.5), а значит, и исходного уравнения (13.4).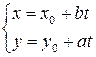 , где
, где 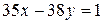 . Поскольку
. Поскольку  , уравнение имеет решение. Рассмотрим дробь
, уравнение имеет решение. Рассмотрим дробь 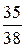 и представим ее в виде цепной дроби:
и представим ее в виде цепной дроби: 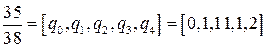 . В этом случае
. В этом случае 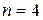 . Поскольку n – четное число, представим дробь
. Поскольку n – четное число, представим дробь  .
.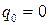


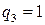

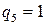
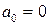



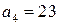


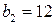

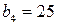
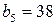
 . Тогда общее решение уравнения имеет вид:
. Тогда общее решение уравнения имеет вид: 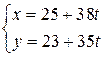 , где
, где 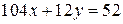 . (13.6)
. (13.6)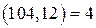 и
и 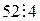 уравнение (13.6) имеет решение. Разделим обе части уравнения на 4, получим уравнение, равносильное исходному,
уравнение (13.6) имеет решение. Разделим обе части уравнения на 4, получим уравнение, равносильное исходному,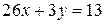 . (13.7)
. (13.7) 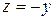 , тогда уравнение (13.7) можно записать в виде:
, тогда уравнение (13.7) можно записать в виде: . (13.8)
. (13.8) . (13.9)
. (13.9) 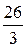 и представим ее в виде
и представим ее в виде 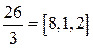 . В этом случае
. В этом случае  . Поскольку n – четное число, представим дробь
. Поскольку n – четное число, представим дробь  .
.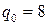
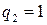
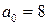


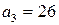
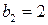

 . Тогда частное решение уравнения (13.8) имеет вид:
. Тогда частное решение уравнения (13.8) имеет вид: 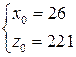 , а общее решение этого уравнения:
, а общее решение этого уравнения:  ,где
,где 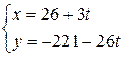 , где
, где  , где
, где 


