
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модулярная арифметика. Сравнения по модулю, их
свойства. Определение 7.1. Рассмотрим целые числа Этот факт обозначают следующим образом: Пример. Следующая теорема устанавливает очевидное необходимое и достаточное условие сравнимости чисел по модулю. Теорема 7.1 (признак сравнения по модулю). Для того, чтобы целые числа Доказательство. Необходимость. Пусть Достаточность. Пусть Следствие. Если Доказательство. Справедливость данного утверждения следует из того, что
Свойства сравнений по модулю.
Рассмотрим сначала свойства сравнений, не зависящие от модуля. 1. Бинарное отношение Доказательство. Доказательство этого утверждения следует непосредственно из определения сравнения по модулю. 1) Рефлексивность: 2) Симметричность: 3) Транзитивность: Отношение эквивалентности Пример. Положим
Классы вычетов по модулю m обычно обозначаются 2. Сравнения по одному и тому же модулю можно почленно складывать:
Доказательство. По определению сравнения по модулю
Тогда 3. Сравнения по одному и тому же модулю можно почленно вычитать:
Доказательство этого свойства аналогично доказательству предыдущего. 4. К обеим частям сравнения можно прибавлять одно и то же число:
Доказательство этого утверждения следует непосредственно из признака сравнения по модулю. Следствие. Члены сравнения можно переносить из одной части в другую с противоположным знаком.
5. Сравнения по одному и тому же модулю можно почленно перемножать: Доказательство. По определению сравнения по модулю
Тогда Следствия. 1) Обе части сравнения можно возводить в одну и ту же целую неотрицательную степень: Доказательство этого утверждения следует из того факта, что возведение числа в натуральную степень означает кратное умножение этого числа на самого себя. При 2) Обе части сравнения можно умножать на одно и тоже целое число: Доказательство этого утверждения непосредственно следует из свойства 5 и из рефлексивности свойства сравнения по модулю: Рассмотрим теперь свойства сравнений, зависящие от модуля. 6. Если числа Доказательство. Пусть 7. Если Доказательство. 8. Пусть два числа сравнимы по модулю m и k – общий делитель этих чисел. Пусть d – наибольший общий делитель чисел m и k. Если данные числа разделить на k, то частные от деления будут сравнимы по модулю
Доказательство. По свойству НОД (§ 3, теорема 3) имеем:
Поскольку Следствия. 1) Обе части сравнения и модуль можно разделить на их общий делитель: Доказательство следует из того, что 2) Обе части сравнения можно разделить на их общий делитель, если он взаимно прост с модулем: Доказательство следует непосредственно из утверждения теоремы. Примеры. 1) Cравнение 2) Рассмотрим верное сравнение Рассмотрим примеры решения задач с использованием свойств сравнения по модулю.
1) Доказать, что число Найдем остаток от деления числа 839 на 7:
Следовательно, 2) Найти остаток от деления числа Найдем сначала остаток от деления
Теперь найдем остаток от деления
Сложим найденные остатки: Таким образом, мы получили, что искомый остаток равен 2 Простые числа Определение 8.1. Натуральное число называется простым, если оно имеет ровно два различных делителя. Если натуральное число имеет больше двух различных делителей, то оно называется составным. Из определения следует, что число 1 не является ни простым, ни составным. Теорема 8.1. Наименьший делитель составного числа, отличный от 1, является простым числом. Доказательство. Рассмотрим составное число n. Расположим его делители в порядке возрастания: Введем понятие канонического разложения натурального числа. Если число n простое, то оно по определению является своим каноническим разложением. Рассмотрим процесс разложения на множители составного числа n. По теореме 8.1 наименьший делитель числа n, отличный от 1, является простым числом. Обозначим его Заметим, что число 1 не будучи ни простым, ни составным числом, не имеет канонического разложения. Нетрудно убедиться в том, что всякое натуральное число, отличное от 1, имеет каноническое разложение, причем единственное. Теорема 8.2 (Евклида). Множество простых чисел бесконечно. Доказательство. Предположим, что утверждение теоремы неверно: множество простых чисел конечно и p – самое большое простое число. Рассмотрим число
Простые числа играют важную роль при решении ряда практических задач, более подробно об этом речь пойдет ниже (см. §§17, 18). Поэтому важно уметь определять, является ли данное число простым или нет. Следующая теорема облегчает в некоторых случаях проверку чисел на простоту. Теорема 8.3. Если число n составное, то в его каноническом разложении найдется хотя бы одно простое число Доказательство. Рассмотрим каноническое разложение числа n:
Следствие. Если Доказательство следствия следует непосредственно из утверждения теоремы. Пример. Докажем, что число 1051 – простое. Для этого проверим, делится ли 1051 на простые числа, не превосходящие
Функция Эйлера Определение 9.1. Функцией Эйлера называется функция Примеры. 1) Найдем 2) Найдем 3) Очевидно, что Вычисление значений функции Эйлера от числа по ее определению не всегда просто, так как требует проверки на взаимную простоту с данным числом всех чисел, не превосходящих это число. Следующая теорема дает удобную формулу для вычисления значения функции Эйлера от числа при помощи его канонического разложения. Теорема 9.1. Пусть n – натуральное число, отличное от 1. Рассмотрим его каноническое разложение: Доказательство. Рассмотрим последовательность натуральных чисел: 1, 2,…, n. Вычеркнем из этой последовательности все числа, которые делятся на
Теорема доказана. Примеры. Вычислим значения функции Эйлера, используя формулу из теоремы. 1) 2) 3) Заметим, что по данной формуле вычислить значение
Свойства функции Эйлера.
1. Если p – простое число, а k – натуральное число, то Доказательство. По теореме 9.1 2. Мультипликативное свойство функции Эйлера. Если числа n и m взаимно просты, то Доказательство. Рассмотрим канонические разложения чисел n и m:
поскольку все сомножители данного произведения различны, что следует из взаимной простоты чисел n и m. По теореме 9.1
Теорема 9.2 (Эйлера). Рассмотрим натуральные числа Доказательство. 1) Прежде всего, заметим, что в случае, когда 2) Будем далее считать, что ……………..
3) Докажем, что все остатки неверно. Предположим, например, что
Отсюда следует, что 4) Докажем, что все остатки взаимно просты с m. Пусть это утверждение неверно. Предположим, например, что При этом 5) Таким образом, мы получили, что числа взаимно просты с числом m, значит, это те же самые числа, что и Систему равенств (9.1) можно привести к виду: ……………….. Перемножая левые и правые части сравнений (9.2), получим: Поделив обе части (9.3) на Теорема 9.3 (Ферма). Пусть p – простое число, и натуральное число a не делится на p. Тогда
Доказательство. Доказательство теоремы непосредственно следует из теоремы Эйлера. Действительно, если число a не делится на простое число p, то Следствие. В условиях теоремы Ферма Доказательство. Умножив обе части сравнения При помощи теорем Эйлера и Ферма можно находить остатки от деления одного числа на другое, иногда это можно осуществить проще, чем при помощи свойств сравнения по модулю, как это делалось выше. Примеры. 1) Найти остаток от деления числа Положим
2) Найти остаток от деления числа Положим
3) Найти остаток от деления числа Числа 1, 2, 3, 4, 5 и 6 взаимно просты с числом 7. Тогда по теореме Ферма Возведем обе части каждого сравнения в степень 3, получим Сложим правые и левые части сравнений и прибавим к обеим частям по 1, получим
|
|||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 1199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.144.32 (0.12 с.) |
 и
и 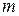 . Если при делении на число
. Если при делении на число 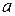 и
и  дают одинаковые остатки, то говорят, что
дают одинаковые остатки, то говорят, что  , или
, или 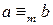 .
. – верно, так как
– верно, так как 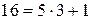 и
и 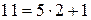 .
.
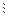
 , где
, где  и
и 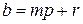 , где
, где 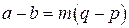 . Поскольку
. Поскольку 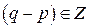 ,
, 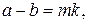 где
где 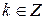 . Разделим число
. Разделим число 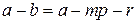 . Следовательно,
. Следовательно,  . Значит, при делении на
. Значит, при делении на 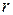 – остаток от деления числа
– остаток от деления числа 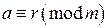 .
.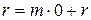 , поскольку
, поскольку 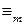 на множестве целых чисел Z является отношением эквивалентности.
на множестве целых чисел Z является отношением эквивалентности. 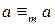 .
.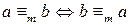 .
.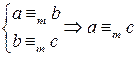 .
. Тогда отношение
Тогда отношение  задает 5 классов вычетов на множестве Z:
задает 5 классов вычетов на множестве Z: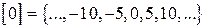 ;
;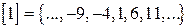 ;
;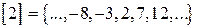 ;
;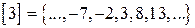 ;
;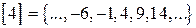 .
.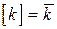 , где
, где 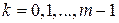 .
.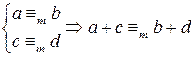 .
.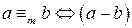
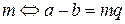 , где
, где 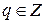 ;
; 
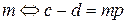 , где
, где 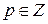 .
.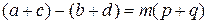 , где
, где 
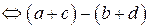
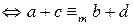 .
. .
. ,
,  .
.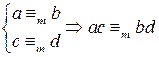 .
.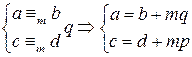 , где
, где 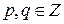 .
.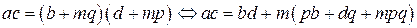 . Поскольку
. Поскольку 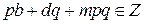 , последнее равенство означает, что
, последнее равенство означает, что 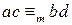 .
.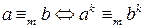 при
при 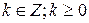 .
.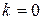 справедливость утверждения очевидна.
справедливость утверждения очевидна.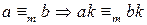 ,
, 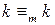 .
.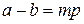 и
и  , где
, где 
 .
.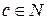 , то
, то 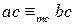 .
.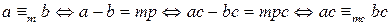 .
.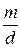 :
: .
.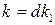 ,
, 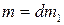 ,где
,где 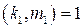 . Тогда
. Тогда 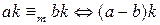
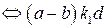


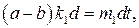

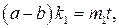

 .
.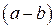
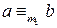 . Но
. Но  , следовательно,
, следовательно,  .
. .
. .
.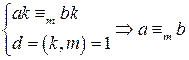 .
. , очевидно, верно. Поскольку
, очевидно, верно. Поскольку 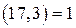 , обе части сравнения можно разделить на 3, полученное сравнение
, обе части сравнения можно разделить на 3, полученное сравнение 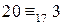 также верно.
также верно.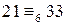 . Числа 21 и 33 имеют общий делитель 3, который не взаимно прост с модулем равным 6. Поэтому применить следствие 2 (т. е. разделить обе части сравнения на 3) нельзя, полученное сравнение
. Числа 21 и 33 имеют общий делитель 3, который не взаимно прост с модулем равным 6. Поэтому применить следствие 2 (т. е. разделить обе части сравнения на 3) нельзя, полученное сравнение 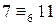 – неверно. Однако, можно применить теорему:
– неверно. Однако, можно применить теорему:  – верное сравнение.
– верное сравнение.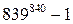 делится на 7.
делится на 7.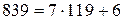 .
.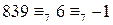 . Тогда по свойствам сравнения по модулю
. Тогда по свойствам сравнения по модулю 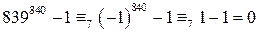 . Это и означает, что
. Это и означает, что 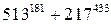 на 11.
на 11.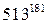 на 11:
на 11: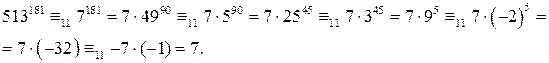
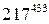 на 11:
на 11:

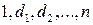 . Докажем, что
. Докажем, что  – простое число. Предположим, что это утверждение неверно, и
– простое число. Предположим, что это утверждение неверно, и 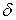 , удовлетворяющее условиям:
, удовлетворяющее условиям: 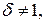
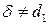 . Поскольку
. Поскольку  и
и  , из транзитивности делимости следует, что
, из транзитивности делимости следует, что 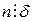 . При этом из свойств делимости (свойства 5) следует, что
. При этом из свойств делимости (свойства 5) следует, что  . Значит, число
. Значит, число  . Тогда
. Тогда 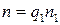 , где
, где 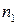 – натуральное число,
– натуральное число, 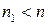 . Если число
. Если число 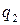 . Тогда
. Тогда 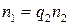 и
и 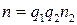 , причем
, причем 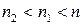 . Если число
. Если число 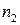 является простым, то процесс закончен. Если число
является простым, то процесс закончен. Если число 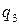 – его наименьший делитель, отличный от 1 и т. д. Продолжая процесс, получим
– его наименьший делитель, отличный от 1 и т. д. Продолжая процесс, получим  , где числа
, где числа 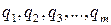 – простые и
– простые и  . Поскольку убывающая последовательность натуральных чисел может содержать только конечное число членов, данный процесс на некотором шаге закончится. Получим разложение числа n на простые множители. Среди них могут оказаться равные, объединяя их и записывая в порядке возрастания, получим каноническое разложение числа n:
. Поскольку убывающая последовательность натуральных чисел может содержать только конечное число членов, данный процесс на некотором шаге закончится. Получим разложение числа n на простые множители. Среди них могут оказаться равные, объединяя их и записывая в порядке возрастания, получим каноническое разложение числа n: 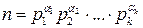 , где числа
, где числа 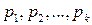 – простые,
– простые, 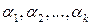 – натуральные.
– натуральные.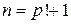 . Поскольку
. Поскольку  , число n – составное. Рассмотрим каноническое разложение числа n:
, число n – составное. Рассмотрим каноническое разложение числа n:  ,
, 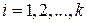 , так как p – самое большое простое число. Очевидно, что
, так как p – самое большое простое число. Очевидно, что  для
для  для
для 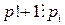 – неверно, поскольку число 1 не делится на
– неверно, поскольку число 1 не делится на 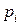 . Значит
. Значит 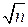 .
. для
для 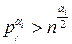 для
для  для
для 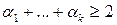 . Действительно, если
. Действительно, если  , то данное утверждение, очевидно, верно. Если же
, то данное утверждение, очевидно, верно. Если же  , то
, то 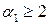 , в противном случае число n было бы простым. Следовательно,
, в противном случае число n было бы простым. Следовательно, 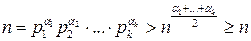 . Полученное противоречие доказывает справедливость утверждения теоремы.
. Полученное противоречие доказывает справедливость утверждения теоремы.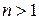 , и n не делится ни на одно простое число, не превосходящее
, и n не делится ни на одно простое число, не превосходящее 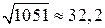 , а именно числа 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31. Как нетрудно установить, число 1051 на перечисленные простые числа не делится, следовательно, является простым.
, а именно числа 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31. Как нетрудно установить, число 1051 на перечисленные простые числа не делится, следовательно, является простым.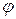 , определенная на множестве натуральных чисел
, определенная на множестве натуральных чисел  , сопоставляющая каждому натуральному числу m количество натуральных чисел, взаимно простых с m и не превосходящих m.
, сопоставляющая каждому натуральному числу m количество натуральных чисел, взаимно простых с m и не превосходящих m. . Для этого выпишем числа, не превосходящие 9 и взаимно простые с 9: 1, 2, 4, 5, 7, 8. Таким образом, получим, что
. Для этого выпишем числа, не превосходящие 9 и взаимно простые с 9: 1, 2, 4, 5, 7, 8. Таким образом, получим, что 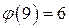 .
. . Поскольку число 11 – простое, все числа, не превосходящие 11, за исключением его самого, взаимно просты с ним, следовательно,
. Поскольку число 11 – простое, все числа, не превосходящие 11, за исключением его самого, взаимно просты с ним, следовательно,  .
.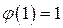 и
и 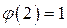 .
.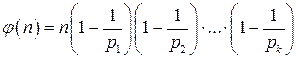 .
.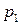 . Таких чисел будет
. Таких чисел будет 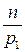 . Останется
. Останется 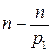 чисел, которые на
чисел, которые на 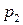 . Их будет
. Их будет 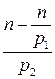 . Останется
. Останется 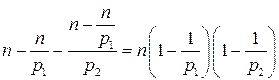 чисел. Продолжая вычеркивать числа, делящиеся на
чисел. Продолжая вычеркивать числа, делящиеся на 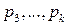 , получим требуемую формулу
, получим требуемую формулу ,
,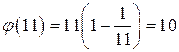 ,
, .
.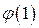 нельзя, так как число 1 не имеет канонического разложения.
нельзя, так как число 1 не имеет канонического разложения. .
.  .
. .
.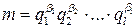 . Тогда каноническое разложение произведения чисел n и m с точностью до порядка сомножителей равно:
. Тогда каноническое разложение произведения чисел n и m с точностью до порядка сомножителей равно: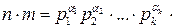
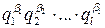 ,
,
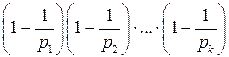
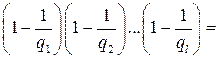
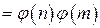 .
.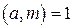 . Тогда
. Тогда 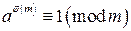 .
.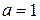 , утверждение теоремы верно для любого числа m. В случае, когда
, утверждение теоремы верно для любого числа m. В случае, когда 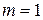 , утверждение теоремы принимает вид:
, утверждение теоремы принимает вид: 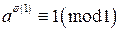 , что, очевидно, также верно для любого числа
, что, очевидно, также верно для любого числа  и
и 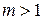 . Выпишем различные натуральные числа, меньшие m и взаимно простые с m:
. Выпишем различные натуральные числа, меньшие m и взаимно простые с m: 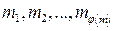 . Рассмотрим произведения
. Рассмотрим произведения 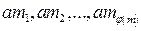 и найдем остатки от деления каждого из этих произведений на m:
и найдем остатки от деления каждого из этих произведений на m: ,
, 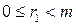 ,
,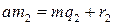 ,
, 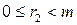 (9.1)
(9.1)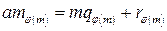 ,
,  .
.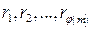 различны. Пусть это утверждение
различны. Пусть это утверждение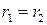 . Тогда, вычитая из первого равенства второе, получим
. Тогда, вычитая из первого равенства второе, получим
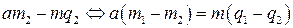 .
. . При этом число a не делится на m, так как числа a и m взаимно просты и
. При этом число a не делится на m, так как числа a и m взаимно просты и 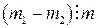 , значит, по свойству делимости 5
, значит, по свойству делимости 5 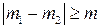 . Но
. Но  и
и 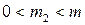 , следовательно,
, следовательно,  . Полученное противоречие доказывает, что сделанное нами предположение о равенстве остатков неверно.
. Полученное противоречие доказывает, что сделанное нами предположение о равенстве остатков неверно.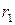 и m не взаимно просты:
и m не взаимно просты:  . Тогда
. Тогда 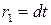 и
и 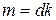 , где
, где 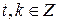 . Но
. Но 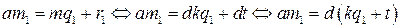 . Тогда
. Тогда 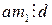 .
. (по определению чисел
(по определению чисел  ), следовательно,
), следовательно,  . Однако, d – общий делитель чисел
. Однако, d – общий делитель чисел 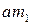 и m, и, как мы предположили,
и m, и, как мы предположили,  . Полученное противоречие доказывает, что сделанное нами предположение, неверно.
. Полученное противоречие доказывает, что сделанное нами предположение, неверно.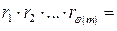
 .
. ,
,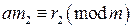 , (9.2)
, (9.2)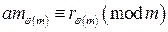 .
.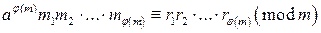 (9.3)
(9.3)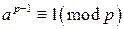 .
.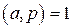 . Тогда по теореме Эйлера
. Тогда по теореме Эйлера  . Но
. Но  , следовательно,
, следовательно, 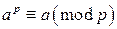 .
. на 7.
на 7.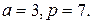 Условия теоремы Ферма выполняются:
Условия теоремы Ферма выполняются: 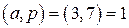 , следовательно,
, следовательно, 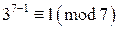 . Возведем обе части сравнения в степень 4, получим
. Возведем обе части сравнения в степень 4, получим 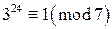 . Поскольку
. Поскольку  ,
,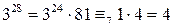 . Значит, остаток от деления числа
. Значит, остаток от деления числа  на 34.
на 34.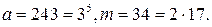 Условия теоремы Эйлера выполняются:
Условия теоремы Эйлера выполняются: 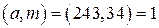 . Вычислим
. Вычислим  . Заметим, что
. Заметим, что 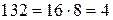 . Тогда по теореме Эйлера
. Тогда по теореме Эйлера 
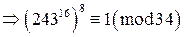 , а
, а 
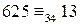 . Значит,
. Значит,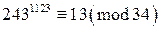 , то есть искомый остаток равен 13.
, то есть искомый остаток равен 13.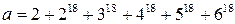 на число
на число 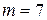 .
. ,
,  ,
, 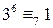 ,
, 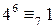 ,
, 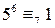 ,
, 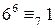 .
.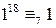 ,
, 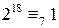 ,
, 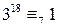 ,
,  ,
,  ,
, 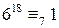 .
. . Следовательно, число a делится на 7 без остатка.
. Следовательно, число a делится на 7 без остатка.


