
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление иррациональных чисел цепными дробями
Пусть w – действительное число. Обозначим целую часть этого числа Рассмотрим число
Обозначим Продолжая этот процесс, получим на шаге n: где Если число w рациональное, то процесс закончится через конечное число шагов. Если число w иррациональное, то процесс будет продолжаться бесконечно долго, в результате чего возникнет бесконечная последовательность натуральных чисел Тогда можно построить бесконечную последовательность подходящих дробей:
Отвлечемся от способа получения последовательности чисел Теорема 14.1. Для любой последовательности целых чисел Доказательство. По свойству 2 подходящих дробей Определение 14.1. Рассмотрим бесконечную последовательность целых чисел Бесконечную цепную дробь можно записать в виде: Теорема 14.2. Всякое иррациональное число может быть представлено в виде бесконечной цепной дроби, притом единственным образом. Доказательство. Пусть
Единственность представления следует из того, что на каждом шаге построения цепной дроби мы выделяем целую часть иррационального числа, что можно сделать единственным образом. Теорема доказана. Заметим, что и наоборот, каждой бесконечной цепной дроби соответствует единственное иррациональное число. Действительно, пусть Примеры. 1) Представим число
Здесь
Заметим, что выражение 2) Представим число
В последней цепной дроби мы получили выражение Поставим теперь обратную задачу: найти по бесконечной периодической цепной дроби равное ей иррациональное число. Пример. Дана бесконечная дробь
При помощи представления иррациональных чисел в виде бесконечных цепных дробей мы можем вычислять их приближения рациональными числами со сколь угодно большой точностью. Как было установлено выше, иррациональное число w принадлежит интервалу, концами которого являются две соседние подходящие дроби. Следовательно, если Следующая теорема дает возможность установить число шагов, за которое можно найти приближение к иррациональному числу с заданной точностью. Теорема 14.3. Пусть w – иррациональное число. Тогда Доказательство. По свойству 2 подходящих дробей имеем:
Таким образом, первая подходящая дробь, которую можно взять в качестве приближенного значения иррационального числа с точностью до 0,1, это дробь
Заметим, что оценка точности, которую дает теорема 14.3, является довольно грубой. Поэтому на практике, вычисляя приближение к иррациональному числу с заданной точностью, можно вычислять последовательно подходящие дроби до тех пор, пока разность между двумя соседними подходящими дробями не станет меньше заданной точности. Тогда в качестве приближения можно взять подходящую дробь с большим номером. Пример. Вычислить с точностью до 0,01 иррациональное число Представим число
Модуль разности
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 840; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.211.87 (0.011 с.) |
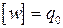 , а дробную часть
, а дробную часть 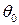 . Таким образом,
. Таким образом,  , где
, где 
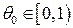 .
. . Поскольку число
. Поскольку число  , его можно представить в виде:
, его можно представить в виде: 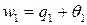 , где
, где 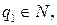
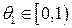 . Тогда
. Тогда  .
. ,
, 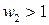 . Выделим целую часть числа
. Выделим целую часть числа 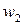 :
: 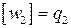 , тогда
, тогда 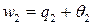 , где
, где 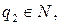
 .
.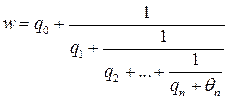 ,
,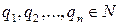 ,
, 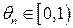 .
. .
. ,
,  , …,
, …, 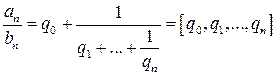 ….
…. . Составим соответствующую последовательность подходящих дробей
. Составим соответствующую последовательность подходящих дробей 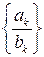 ,
, 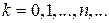 . Справедлива следующая теорема.
. Справедлива следующая теорема.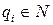 для
для 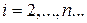 , последовательность подходящих дробей сходится.
, последовательность подходящих дробей сходится. , а из свойства 5 следует, что
, а из свойства 5 следует, что 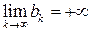 , (так как возрастающая последовательность натуральных чисел не может быть ограниченной). Значит,
, (так как возрастающая последовательность натуральных чисел не может быть ограниченной). Значит,  . А это и означает, что существует конечный
. А это и означает, что существует конечный 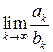 , то есть последовательность подходящих дробей сходится. Теорема доказана.
, то есть последовательность подходящих дробей сходится. Теорема доказана.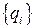 ,
,  , причем
, причем 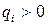 для
для 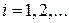 . Составим соответствующую бесконечную последовательность подходящих дробей
. Составим соответствующую бесконечную последовательность подходящих дробей 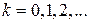 . Бесконечной цепной дробью называется
. Бесконечной цепной дробью называется 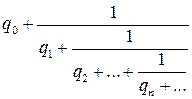 или в виде:
или в виде: 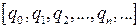 .
.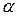 иррациональное число. Положим
иррациональное число. Положим  – целая часть числа
– целая часть числа 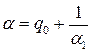 , где
, где 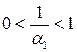 . Тогда
. Тогда 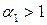 . Заметим, что число
. Заметим, что число 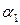 не целое. Действительно, если бы оно было целым, то число
не целое. Действительно, если бы оно было целым, то число 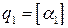 . Отсюда следует, что
. Отсюда следует, что 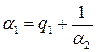 , где
, где 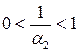 . Тогда, как и выше,
. Тогда, как и выше,  и
и  не является целым. Получим, что
не является целым. Получим, что 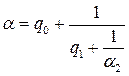 . Будем продолжать этот процесс. Очевидно, что он никогда не закончится, так как в противном случае, оказалось бы, что число
. Будем продолжать этот процесс. Очевидно, что он никогда не закончится, так как в противном случае, оказалось бы, что число 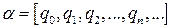 . Тогда, по теореме 14.1 справедливо
. Тогда, по теореме 14.1 справедливо  , а если предел последовательности существует, то он единственен.
, а если предел последовательности существует, то он единственен. в виде бесконечной цепной дроби.
в виде бесконечной цепной дроби.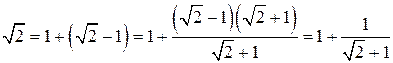 .
.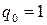 ,
,  . Продолжим процесс вычисления:
. Продолжим процесс вычисления: . Здесь
. Здесь 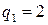 ,
,  .
.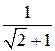 нам встречалось ранее, и мы получили выше, что
нам встречалось ранее, и мы получили выше, что  . Учитывая это, получим, что
. Учитывая это, получим, что 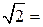
 . Таким образом, получим, что число
. Таким образом, получим, что число  можно представить в виде бесконечной периодической цепной дроби:
можно представить в виде бесконечной периодической цепной дроби: 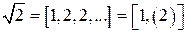 .
.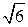 в виде бесконечной цепной дроби.
в виде бесконечной цепной дроби.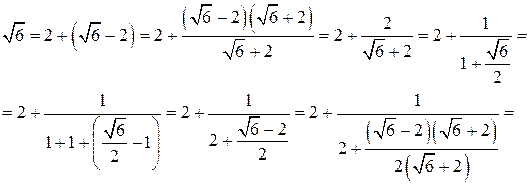
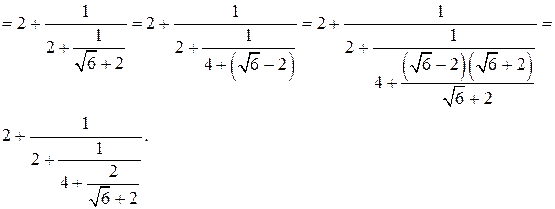
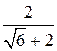 , которое, как мы видим, представимо в виде
, которое, как мы видим, представимо в виде 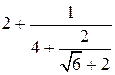 . Таким образом, получили, что
. Таким образом, получили, что 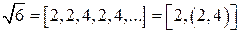 .
.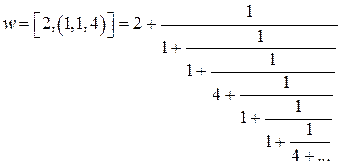 . Тогда
. Тогда  . Таким образом, мы получили уравнение относительно w. Упрощая его, получим квадратное уравнение
. Таким образом, мы получили уравнение относительно w. Упрощая его, получим квадратное уравнение 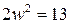 . Учитывая, что число w положительно, получим, что
. Учитывая, что число w положительно, получим, что  .
.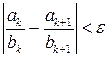 , то
, то 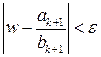 .
.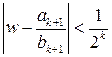 для
для 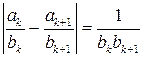 . А по свойству 5:
. А по свойству 5: 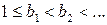 . Следовательно,
. Следовательно, 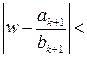
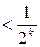 . Теорема доказана.
. Теорема доказана.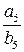 , поскольку
, поскольку  . А если, к примеру, заданная точность равна 0,01, то первой подходящей дробью, которую можно взять в качестве приближения будет
. А если, к примеру, заданная точность равна 0,01, то первой подходящей дробью, которую можно взять в качестве приближения будет 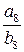 , поскольку
, поскольку  .
. .
.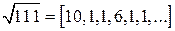 . Выпишем подходящие дроби. Для этого составим таблицу, в последней строке, которой будем записывать разности между соответствующей подходящей дробью и предыдущей:
. Выпишем подходящие дроби. Для этого составим таблицу, в последней строке, которой будем записывать разности между соответствующей подходящей дробью и предыдущей: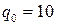

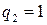
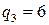



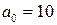
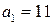
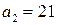

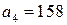
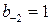
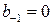
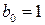

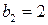

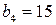
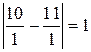 =1
=1
 0,5
0,5
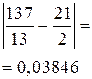
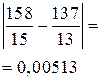
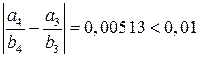 , следовательно, рациональное число
, следовательно, рациональное число  является приближением иррационального числа
является приближением иррационального числа 


