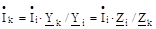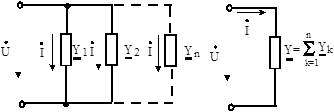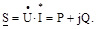Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ланцюг із паралельним з'єднанням елементівСодержание книги
Поиск на нашем сайте
Ланцюг, що складається з елементів активного опору r, індуктивності L і ємності С, з'єднаних паралельно, зображена на рис. 5.5, а.
Рис. 5.5. Ланцюг з паралельним з'єднанням елементів r, L і С і його векторні діаграми Якщо такий ланцюг увімкнути під синусоїдальну напругу u=Um ·sin ωt, то сила струму у нерозгалуженій частині ланцюга буде визначатися за першим законом Кірхгофа:
або
де 1/r, 1/(ωL), ωС відповідно називаються активною, індуктивною і ємнісною провідностями віток і позначаються g, bL і bС . Струми iL та iС зрушені один щодо одного на кут л, тому їхня сума, названа реактивною силою струму, визначиться рівністю:
iр = ILm sin (ωt – 90o) + ICm sin(ωt + 90o) = Iрm sin (ωt ± 90o).
Отже, сила струму у нерозгалуженій частині ланцюга визначиться сумою активної та реактивної сил струмів:
Діюче значення сили струму в нерозгалуженій частині ланцюга відповідно до першого закону Кірхгофа визначиться геометричною сумою векторів:
яку знаходять, використовуючи векторну діаграму струмів, називану трикутником струмів. На рис. 5.5зображені векторні діаграми сил струмів відповідно при Зменшивши, сторони трикутника струмів (див. рис. 5.5,в) у U разів, одержимо трикутник провідностей, подібний до трикутника струмів. Зрушення за фазою між напругою й струмом дорівнює:
У залежності від того, яка провідність переважає в ланцюзі – індуктивна або ємнісна, різниця фаз між напругою і силою струму буде позитивною або негативною: при bL > bC різниця фаз φ>0 і напруга випереджає струм; якщо bL < bC, то φ<0 і струм випереджає напруга; якщо b = 0, то φ= 0. Змішане з'єднання приймачів
Будь-який приймач електроенергії практично може мати два або три параметри одночасно. На рис. 5.6, а представлений ланцюг із двох паралельних віток, одна з яких містить активний опір і індуктивність, а інша – активний опір і ємність. Якщо в такий ланцюг подати синусоїдальну напругу u = Um·sinωt, то сили струмів у паралельних вітках будуть відповідно дорівнювати: i1 = I1m ·sin (ωt –φ1); i2 = I2m ·sin (ωt - φ2 ). Діючі значення сил струмів визначаються за законом Ома. Складова і повна сила струму нерозгалуженої частини ланцюга відповідно запишуться у такий спосіб:
а) б)
Рис. 5.6. Розгалужений ланцюг і його векторна діаграма
Лекція 6 Символічний метод розрахунку електричних Ланцюгів Символічний метод розрахунку ланцюгів перемінного струму, в основу якої покладено зображення синусоїдальних функцій часу комплексними числами, дозволяє рівняння для будь-якого ланцюга, складені на підставі законів Кірхгофа, вирішувати алгебраїчно, аналогічно рівнянням для ланцюгів постійного струму. Це значно спрощує розрахунки ланцюгів перемінного струму, особливо складних ланцюгів. Відомо, що комплексне число може бути записане в трьох основних формах — алгебраїчній, тригонометричній і показовій:
Комплекси, що зображують синусоїдальні величини, прийнято позначати відповідними прописними буквами з рискою внизу або крапкою вгорі, наприклад
Відношення комплексу напруги до комплексу сили струму називається комплексом повного опору, тобто:
де Z- повний опір, чи модуль комплексу повного опору;
Отже, комплекс повного опору може бутипредставлений виразом:
де R и X–відповідно активний і реактивний опори. Відношення комплексу сили струму до комплексу напруги називається комплексом повної провідності, тобто:
де Y — повна провідність ланцюга, чи модуль комплексу повної провідності. Отже, комплекс повної провідності ланцюги може бути виражений співвідношенням:
де Gі B — відповідно активна і реактивна провідності ланцюга. У символічній формі можуть бути представлені також повна, активна і реактивна потужності. Для цього при відомих комплексах напруги й сили струму
Отже, модуль комплексу S визначає повну потужність, дійсна частина – активну, а уявна – реактивну. Закон Ома для ланцюгів перемінного струму в символічній формі може бути представлений у наступному виді:
Ці співвідношення справедливі для всякого лінійного ланцюга і для будь-якої його ділянки. Перший закон Кірхгофа в символічній формі запису говорить: алгебраїчна сума комплексів сил струмів, що сходяться у вузлі електричного ланцюга, дорівнює нулю:
Другий закон Кірхгофа в символічній формі для будь-якого замкнутого контуру записується у виді рівняння:
таким чином, алгебраїчна сума комплексів ЕРС, що діють у контурі, дорівнює алгебраїчній сумі комплексів падінь напруг на всіх ділянках цього контуру.. При складанні рівнянь за законами Кірхгофа правила знаків для комплексів сил струмів, ЕРС і напруг ті ж, що і для векторів. Розглянемо теоретичний розрахунок деяких ланцюгів перемінного струму. Нехай електричний ланцюг, зображений на рис. 6.1, а, знаходиться під синусоїдальною напругою На підставі другого закону Кирхгофа рівняння електричної рівноваги ланцюга для комплексних величин запишеться так:
Вирішуючи це рівняння щодо комплексу діючого значення сили струму, одержимо:
де
а) б) в)
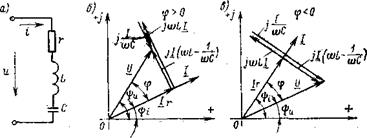
Рис. 6.1. Нерозгалужений ланцюг з елементами R, L и С та його векторні діаграми
Аргумент ф і модуль Z, комплексу повного опору знаходяться з виразів:
Комплекс потужності визначається формулою:
На мал. 6.1, б, в для розглянутого ланцюга побудовані векторні діаграми. Якщо нерозгалужений ланцюг складається з n послідовно з'єднаних ділянок, комплекси повних опорів яких Z, Z2, Zз і знаходиться під синусоїдальною напругою
де З рівняння (6.13) знаходимо комплекс сили струму:
Комплекс потужності розглянутого електричного ланцюга можна знайти, множачи комплекс напруги
Якщо ланцюг складається з п рівнобіжних (паралельних) віток, комплекси повних провідностей яких Y, Y,. -., Yn(мал. 6.2), то, на підставі першого закону Кірхгофа, комплекс сили струму у нерозгалуженій частині ланцюга визначиться виразом:
де Наслідком першого закону Кірхгофа є співвідношення:
тобто сила струму у вітках прямо пропорційна їхнім комплексам повних провідностей і обернено пропорційна комплексам повних опорів.
Рис. 6.2 Паралельне з'єднання елементів
Комплекс потужності розгалуженого електричного ланцюга визначається виразом:
ЛЕКЦІЯ 7
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 98; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

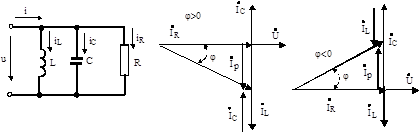 а) б) в)
а) б) в) 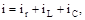
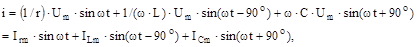
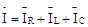
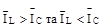 . При
. При 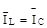 вектори сили струму й напруги збігаютьсяза фазою.
вектори сили струму й напруги збігаютьсяза фазою.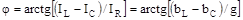
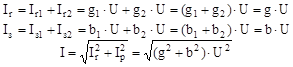
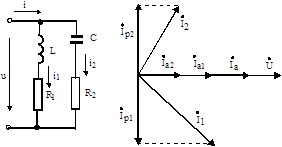
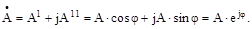
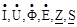 . Таким чином, якщо сила струму і напруга синусоїдальні, тобто
. Таким чином, якщо сила струму і напруга синусоїдальні, тобто 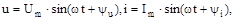 то відповідні їм комплекси амплітуд і діючих значень запишуться так:
то відповідні їм комплекси амплітуд і діючих значень запишуться так: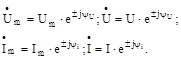
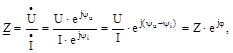
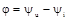 – кут зрушення між векторами напруги і сили струму.
– кут зрушення між векторами напруги і сили струму.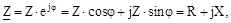
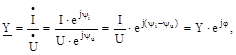
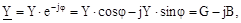
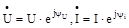 треба помножити комплекс напруги на сполучений комплекс сили струму
треба помножити комплекс напруги на сполучений комплекс сили струму 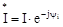 :
: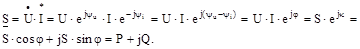
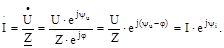
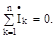
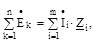
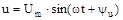 . Визначимо силу струму в ланцюзі, а також побудуємо векторні діаграми для індуктивного (φ>0) і ємнісного (φ<0) характеру опору, представлені відповідно на мал. 6.1, б, в.
. Визначимо силу струму в ланцюзі, а також побудуємо векторні діаграми для індуктивного (φ>0) і ємнісного (φ<0) характеру опору, представлені відповідно на мал. 6.1, б, в.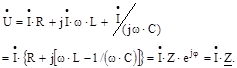

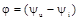 – початкова фаза сили струму.
– початкова фаза сили струму.
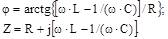

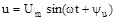 , то по другому закону Кірхгофа можна записати:
, то по другому закону Кірхгофа можна записати: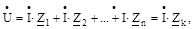
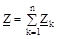 , тобто комплекс повного опору нерозгалуженого ланцюга дорівнює алгебраїчній сумі комплексів повних опорів ділянок ланцюга.
, тобто комплекс повного опору нерозгалуженого ланцюга дорівнює алгебраїчній сумі комплексів повних опорів ділянок ланцюга.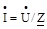
 на сполучений комплекс сили струму
на сполучений комплекс сили струму 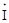 :
: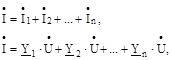
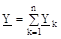 , тобто комплекс еквівалентної провідності розгалуженого ланцюга дорівнює алгебраїчній сумі комплексів повних провідностей віток.
, тобто комплекс еквівалентної провідності розгалуженого ланцюга дорівнює алгебраїчній сумі комплексів повних провідностей віток.