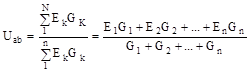Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок ланцюгів оснований на перетворені трикутника опорів в еквівалентну зірку та навпакиСодержание книги
Поиск на нашем сайте
З’єднання трьох елементів ланцюга Ra, Rb, Rc, яке має вигляд зірки з трьома променями зі спільною точкою – вузлом у центрі, має назву "зірка" (рис. 2.5, а). З’єднання цих самих елементів, які утворюють сторони трикутника, мають назву "трикутник" (рис. 2.5, б). Трикутник опорів і відповідна йому зірка є еквівалентними, якщо у схемі, при всіх режимах її роботи, заміна одного з’єднання іншим не змінює струми в усіх інших ділянках і потенціали у вузлових точках.
а) б)
Рис. 2.5. З’єднання опорів "зіркою" та "трикутником"
Перетворення трикутника опорів в еквівалентну зірку (рис. 2.6) проводиться на підставі наступних співвідношень:
Рис. 2.6. Схема перетворювань Таким чином, опір будь якого променя еквівалентної зірки дорівнює здобутку двох опорів трикутника, які з цим вузлом, поділеному на суму всіх трьох опорів трикутника. Перетворення зірки опорів в еквівалентний трикутник проводиться на підставі наступних співвідношень:
ЛЕКЦІЯ 3 СКЛАДНІ ЛАНЦЮГИ Й МЕТОДИ ЇХНЬОГО РОЗРАХУНКУ Складні з'єднання мають різні електричні ланцюги, наприклад, ланцюги систем автоматики, ланцюги електронних пристроїв і ланцюги електропостачання. У таких ланцюгах, як правило, відомі опори і ЕРС, а потрібно визначити сили струмів, напруги й потужності окремих віток. Найбільш складна задача – це розрахунок сил струмів у вітках ланцюгів. Розрахунок складних ланцюгів роблять методами контурних струмів, накладення, вузлових потенціалів або еквівалентного генератора. Суть цих методів полягає в розв’язанні системи незалежних рівнянь, складених за законами Кірхгофа. Якщо складний ланцюг (рис. 3.1) складається з p віток і q вузлів, то в ньому є тільки (q-1) незалежних вузлів і n=(p - q+1) незалежних контурів. Тому можна скласти за першим законом Кірхгофа q—1 і за другим n = p - q+1 незалежних рівнянь.
Рис. 3.1 Принципові схеми складних ланцюгів Метод контурних струмів
Метод зводиться до розв’язання системи n = p – q + 1 рівнянь, складених за другим законом Кірхгофа для незалежних контурів ланцюга. У результаті рішення визначаються сили струмів, що протікають по незалежних контурах, звані контурними силами струмів. Дійсні ж сили струмів у вітках знаходяться як алгебраїчна сума відповідних контурних сил струмів. На рис. 3.2 зображено складний ланцюг, що має шість віток і чотири вузли. Для визначення сил струмів у вітках ланцюга визначаємо число незалежних контурів n=p-q+1=6-4+1=3. Вибравши контури та задавши у них напрямки контурних струмів J 1, J 2, J 3, як зазначено на рисунку стрілками, складемо рівняння за другим законом Кірхгофа:
У цих рівняннях прийнято називати й позначати: а) суму всіх опорів кожного контуру – власним опором контуру:
R11 = R1 + R3 + R5; R22 = R2 + R3 + R6; R33 = R4 + R5 + R6;
Рис. 3.2. Схема ланцюга до розрахунку методом контурних струмів
б) опір спільної вітки двох контурів — взаємним опором контурів; він вважається позитивним, якщо контурні струми в ньому збігаються по напрямку, і негативним, якщо контурні струми в цьому опорі протилежні за напрямком:
R12 = R21 = R3; R13 = R31 = R5; R23 = R32 = R6;
в) алгебраїчну суму ЕРС у контурі — контурною ЕРС:
E11 = E1 + E3; E22 = E2 + E3; E33 = E4.
З урахуванням уведених позначень рівняння (3.1) перепишуться у такий спосіб:
3.2. Метод вузлових потенціалів
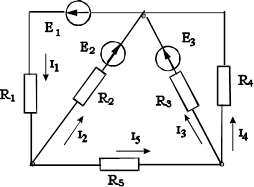
Метод зводиться до визначення потенціалів окремих вузлів складного електричного ланцюга шляхом розв’язання системи рівнянь, складених за першим законом Кірхгофа. Застосування цього методу дозволяє зменшити кількість рівнянь до числа "Y", що дорівнює кількості вузлів без одного: Y= N – 1. При написанні рівнянь один із вузлів приймають за опорний і потенціал його вважають рівним нулеві, а потенціали інших вузлів (вузлових потенціалів) визначають шляхом розв’язання системи рівнянь. Після знаходження вузлових потенціалів сили струмів у вітках визначають за законом Ома або виходячи з другого закону Кірхгофа. Розглянемо застосування методу до розрахунку складних ланцюгів. Нехай будь-який лінійний ланцюг (рис. 3.3) має три вузли і п'ять віток. Виберемо довільно опорний вузол і позначимо його через 0, а інші вузли – цифрами 1 і 2. Потенціал точки 0, φ0 = 0 В. Система рівнянь у загальному виді буде такою:
Тут
Рис. 3.3. Схема ланцюга до розрахунку методом вузлових потенціалів
У випадку двох вузлів А і В у ланцюзі вузлова напруга Uав визначиться за виразом:
У рівнянні 3.3 добутки ЕkGk беруться зі знаком "+", якщо ЕРС направлені від вузла А до вузла В. Струми розраховуються за законом Ома або виходячи з другого закону Кірхгофа.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.61.96 (0.01 с.) |

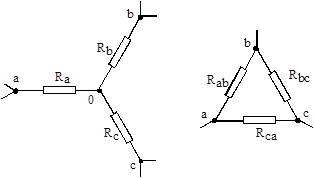
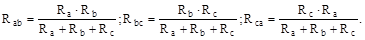

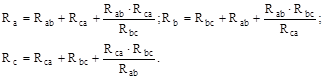

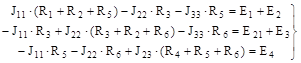

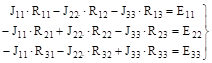
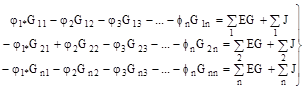
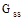 – сума провідностей віток, підключених до вузла s, а Gqs – сума провідностей віток, ізо з'єднують вузол s з вузлом q;
– сума провідностей віток, підключених до вузла s, а Gqs – сума провідностей віток, ізо з'єднують вузол s з вузлом q;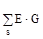 – алгебраїчна сума здобутків віток, приєднаних до вузла s, причому "+", якщо ЕРС спрямована до вузла s, "-" – якщо від вузла;
– алгебраїчна сума здобутків віток, приєднаних до вузла s, причому "+", якщо ЕРС спрямована до вузла s, "-" – якщо від вузла;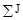 - алгебраїчна сума джерел струму, приєднаних до вузла s, причому "+", якщо J спрямована до вузла s, "-" – якщо від вузла.
- алгебраїчна сума джерел струму, приєднаних до вузла s, причому "+", якщо J спрямована до вузла s, "-" – якщо від вузла.