
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прості ланцюги й методи їхнього розрахункуСодержание книги
Поиск на нашем сайте
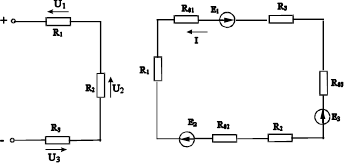
Простими ланцюгами постійного струму називають ланцюги з послідовним, паралельним або змішаним з'єднанням їхніх параметрів. Для розрахунку таких ланцюгів використовують закон Ома і так звані еквівалентні перетворення. Суть останніх полягає у тому, що на окремих ділянках ланцюга ряд елементів заміняється одним еквівалентним за умови незмінності струму й напруги у не перетворених ділянках ланцюга. У результаті спрощується вихідний ланцюг і, отже, процес його розрахунку. На рис. 2.3 приведені два можливих варіанти нерозгалуженого ланцюга. В одному ланцюзі (рис. 2.3, а) послідовно з'єднані тільки опори, а в іншому (рис. 2.3, б) – усі елементи. Струм у кожному ланцюзі визначається за законом Ома. Звідси очевидно наступне: а) у нерозгалуженому ланцюзі при з'єднанні n опорів:
тобто еквівалентний опір послідовно з'єднаних опорів дорівнює сумі цих опорів;
а) б)
Рис. 2.3. Схеми нерозгалужених ланцюгів б) у нерозгалуженому ланцюзі при з'єднанні m генераторів напруги:
тобто ЕРС еквівалентного джерела напруги дорівнює алгебраїчній сумі ЕРС, а його внутрішній опір дорівнює сумі внутрішніх опорів усіх джерел напруги, з'єднаних послідовно; в) спадання напруги на окремих ділянках нерозгалуженого ланцюга пропорційні їхнім опорам:
г) потужність ланцюга дорівнює сумі потужностей окремих її елементів. На рис. 2.4, априведена типова схема паралельного з'єднання споживачів. Напруга на затисках усіх віток однакова і дорівнює:
а) б)
Рис. 2.4. Схеми розгалужених ланцюгів споживачів (a) і джерел напруги (б) Сила струму I у нерозгалуженій частині ланцюга відповідно до першого закону Кірхгофа дорівнює: I = I1 + I2 + I3 =U/R1+ U/R2 + U/R3 = U (G1 + G2 +G3). Звідси випливає, що при рівнобіжному з'єднанні споживачів, що містять тільки опір, мають місце наступні співвідношення: а) еквівалентна провідність ланцюга дорівнює
де n — число споживачів;
б) сила струму кожної вітки споживача визначається виразом:
In = ∑ U · Gk; в) потужність ланцюга дорівнює сумі потужностей окремих споживачів: P = ∑ U2 · Gk.
Особливість паралельного з'єднання у тому, що всі вітки ланцюга знаходяться під однаковою напругою й режим роботи кожної не залежить від інших. Практичний інтерес являє рівнобіжне з'єднання джерел напруги, що працюють на загальне навантаження. На рис. 2.4, б представлена схема рівнобіжного з'єднання двох джерел напруги. Для цього ланцюга, у відповідності з другим законом Кірхгофа, одержуємо:
Рівняння (2.12) називаються рівняннями паралельної роботи джерел напруги. Аналізуючи їх, можна зробити наступні висновки: якщо ЕРС одного джерела напруги буде менше напруги U, то він перейде в режим споживача; якщо ЕРС і внутрішні опори паралельно працюючих джерел рівні, то будь-який струм навантаження розподілиться між джерелами рівномірно; якщо ЕРС паралельно працюючих джерел напруги рівні, а внутрішні опори різні або, навпаки, ЕРС не рівні, а внутрішні опори однакові, то через джерело з меншим внутрішнім опором і джерелом із більшою ЕРС буде проходити більший струм.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 57; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.76 (0.01 с.) |

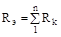 ,
,

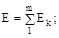
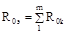 ,
,
 ;
;
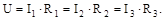
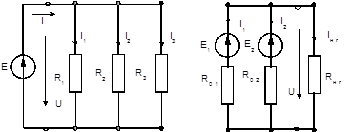
 ,
,



