
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи для контроля по модулю 2Содержание книги
Поиск на нашем сайте
ВАРИАНТ 1 Задача 1 Срочный аннуитет пренумерандо в размере 300 грн. вносится по полугодиям. Найти сумму через 5 лет. Процентная ставка – 12 %. Начисление процентов ежеквартальное. Задача 2 Продисконтировать поток платежей постнумерандо. Характеристика потока: 1 год – 500 грн. – поступление; 2 год – 200 грн. – поступление; 3 год – 400 грн. – выплата. Далее, в течение следующих семи лет, - поступления по 500 грн. Ставка дисконта 6%. Задача 3 В конце каждого года в банк вносится 3000 грн. под 16% годовых. Определить сумму, которая будет на счету клиента через 6 лет, если начисление процентов один раз в два года. ВАРИАНТ 2 Задача 1 В начале каждого полугодия в банк на депозитный счет поступает 2000 грн. под 12% годовых. Определить сумму, которая будет на счету клиента через 5 лет, если начисление процентов ежеквартальное. Задача 2 Продисконтировать поток платежей пренумерандо, если первые три года поступления составляли по 300 грн. В 4-м году изъяли 1000 грн. В последующие 4 года поступали по 400 грн. Ставка дисконта – 8%. Задача 3 Срочный аннуитет постнумерандо в размере 500 грн. вносится ежеквартально. Найти сумму через 4 года. Процентная ставка – 8 %. Начисление процентов по полугодиям. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ по подготовке к модулю №3 По курсу «Деньги и кредит» ССУДА С ФИКСИРОВАННОЙ ВЫПЛАТОЙ Платеж РАВНЫМИ ЧАСТЯМИ в конце обусловленных периодов k начисляется как сложный процент на невозвращенный остаток, рассчитывается по формуле: (14) где PV — основная сумма долга, сумма взятого кредита, ссуды; P* — фиксированная выплата, которая выплачивается k раз; i — процентная ставка в каждом из периодов k; k — количество периодов, в конце которых возвращается сумма P*. Ö ЗАПОМНИТЕ: ФОРМУЛА (14) ПРИМЕНЯЕТСЯ ТОЛЬКО В СЛУЧАЕ, КОГДА ПЕРИОДЫ НАЧИСЛЕНИЯ ПРОЦЕНТОВ СОВПАДАЮТ С ПЕРИОДАМИ ВЫПЛАТЫ ФИКСИРОВАННОЙ ВЕЛИЧИНЫ Р*. ДРУГИМИ СЛОВАМИ, ЕСЛИ ВЫПЛАТЫ Р* В КОНЦЕ КАЖДОГО ГОДА, ТО НАЧИСЛЕНИЕ ПРОЦЕНТОВ – ЕЖЕГОДНОЕ, ЕСЛИ ВЫПЛАТЫ Р* – КАЖДЫЕ ПОЛГОДА, ТО НАЧИСЛЕНИЕ ПРОЦЕНТОВ ТОЖЕ КАЖДЫЕ ПОЛГОДА, ЕСЛИ ВЫПЛАТЫ Р* - ЕЖЕКВАРТАЛЬНЫЕ, ТО НАЧИСЛЕНИЕ ПРОЦЕНТОВ – КВАРТАЛЬНОЕ. ТОЛЬКО ПРИ ЭТИХ УСЛОВИЯХ ФОРМУЛА (14) ДАЕТ ПРАВИЛЬНЫЙ РЕЗУЛЬТАТ.
Формула (14) может быть записана в другой форме:
Рассмотрим использование формулы (14) на примере задачи №9. Задача 9 Вы заняли на 4 года 10000 грн. под 14%, которые насчитываются по схеме сложных процентов на невозвращенный остаток. Возвращать необходимо равными частями в конце каждого года. Найти размер годового платежа. Стратегия решения задачи Анализ задачи показывает, что количество возвратов фиксированной суммы Р* равно четырем, т.е. k = 4. Начисление процентов – ежегодное, сложное. Процентная ставка – годовая. Необходимо найти такую величину Р*, чтобы, возвращая ее четыре раза (в конце каждого года), возвратить долг (кредит, ссуду) в размере 10000 грн., и возвратить проценты, которые начисляются на остаток после каждой выплаты Р*. Решение задачи

   Рисунок 5 Рисунок 5
На рис. 5 точка 1 – это сумма кредита, которую взяли вначале 4-х летнего срока. Точка 2 - это сумма долга в конце первого года. Сумма долга в точке 2 состоит из суммы 10000 грн. плюс проценты, которые начислены за год на сумму 10000 грн. Рассчитывается FVточка 2 = 10000 грн. + 10000 грн. 0,14 = 11400 грн., или, что одно и то же, FVточка 2 = 10000 грн. (1+0,14) = 11400 грн. Далее, в точке 2 (это конец первого года) пришло время возвратить фиксированную сумму Р* в размере 3432 грн. После возврата фиксированной суммы (3432 грн.) в конце первого года непогашенный остаток равен 11400 грн. – 3432 грн. = 7968 грн. (точка 3 на рис. 5). На этот непогашенный остаток в размере 7968 грн. в течение второго года начисляется процент по ставке 14%. Следовательно, долг на конец второго года равен FVточка 4 = 7968 грн. (1+0,14) = 9083 грн. Величина 9083 грн. (точка 4 на рис. 5) – это сумма долга на конец второго года. После выплаты фиксированной суммы (3432 грн.) на конец второго года непогашенный остаток составляет 9083 грн. – 3432 грн. = 5651 грн., что отражено в точке 5 на рис. 5. Аналогично рассчитываются величины в точках 6, 7, 8, 9. Точка 6 – величина суммы долга в конце третьего года (6442 грн.). Точка 7 – непогашенный остаток в конце третьего года (3010 грн.). Точка 8 – сумма долга на конец четвертого года (3432 грн.). Точка 9 – сумма долга на конец четвертого года (0 грн.).
Графическая иллюстрация задачи показывает, что найденная по формуле (14) величина фиксированной выплаты в размере Р* = 3432 грн. вычислена верно, т. к. в конце четвертого года сумма долга равна нулю. Ответ: размер годового платежа Р* = 3432 грн.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.7.190 (0.009 с.) |

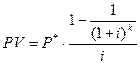 (14)
(14)



