
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постоянная времени обмотки управления дросселя управления Тдр.Содержание книги
Поиск на нашем сайте
Постоянная времени Т др ориентировочно принимается в пределах:
Принимаем
Коэффициент передачи дросселя управления Коэффициент передачи
где
Приближенно фазный ток дросселя определяется из векторной диаграммы токов вторичной (выходной) обмотки трансформатора (рис.4.3).

Векторная диаграмма тока дросселя в режиме холостого хода:
Следовательно:
Векторная диаграмма тока дросселя в режиме номинальной нагрузки: Фазный ток вторичной (выходной) обмотки ТФК при номинальной нагрузке генератора определяется как:
Следовательно:
Расчет и выбор параметров корректора напряжения Коэффициент передачи измерительного органа Коэффициент передачи
Коэффициент усиления полупроводникового усилителя Коэффициент усиления
Коэффициент передачи гибкой обратной связи Коэффициент
Принимаем ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ САРВ СГ Важнейшей задачей анализа динамических систем управления является решение вопроса об их устойчивости. Техническое понятие устойчивости систем автоматического управления отражает свойство технической системы не только стабильно работать в нормальных режимах, но и "не уходить вразнос" при отклонении всевозможных параметров системы от номинала и влиянии на систему дестабилизирующих воздействий, т. е. отражает способность системы возвращаться к равновесному состоянию, из которого она выводится возмущающими или управляющими воздействиями. Устойчивость системы - техническое требование в ряду более сложных требований, связанных с показателями качества и точности САУ. Необходимые и достаточные условия дает алгебраический критерий Гурвица.
Критерий Гурвица Швейцарский математик А. Гурвиц предложил критерий для определения устойчивости линейных автоматических систем любого порядка. Критерий Гурвица, отличающийся простотой и наглядностью, получил широкое распространение. Исходной информацией для использования этого критерия является характеристическое уравнение исследуемой системы. Для системы любого порядка можно получить выражения условий устойчивости. С увеличением порядка характеристического уравнения условия устойчивости усложняются. Практически для решения задачи синтеза критерий Гурвица используется лишь для систем не выше четвертого порядка. Для системы второго порядка условия устойчивости следующие:
Характеристическое уравнение второго порядка имеет вид:
Чтобы его получить, необходимо найти характеристический полином замкнутой системы.
где k = k ио k в k у k др k г;
Условия устойчивости:
Условия выполняются, следовательно, данная система является устойчивой.
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.183.204 (0.006 с.) |

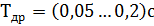 .
.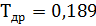 с.
с.
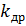 может быть ориентировочно определен как:
может быть ориентировочно определен как: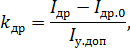
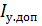 - наибольший ток обмотки управления, принимаемый из неравенства:
- наибольший ток обмотки управления, принимаемый из неравенства: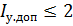 А. Принимаем
А. Принимаем  А;
А;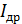 ,
,  – фазный ток дросселя управления в номинальном режиме и в режиме холостого хода соответственно.
– фазный ток дросселя управления в номинальном режиме и в режиме холостого хода соответственно.
 А.
А.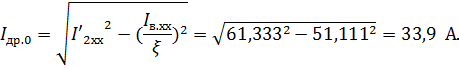

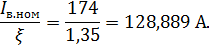
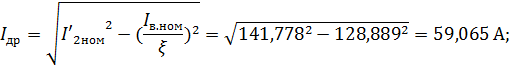
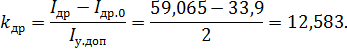
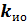
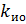 может быть определен как:
может быть определен как: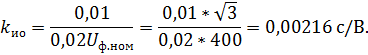

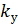 может быть определен как:
может быть определен как: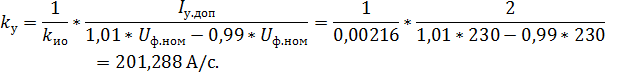

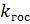 принимается ориентировочно в пределах:
принимается ориентировочно в пределах: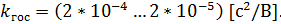
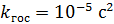 /В.
/В.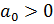 ;
; 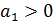 ;
; 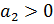 .
.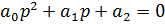 .
.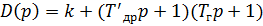 ,
,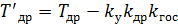 ;
;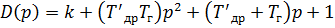 .
.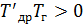 ;
;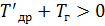 ;
;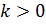 .
.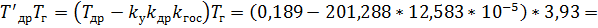
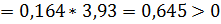 ;
;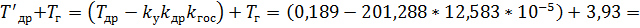
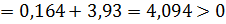 ;
;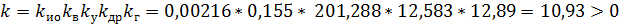 ;
;


