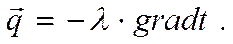Температурное поле. Тепловой поток.

 

 

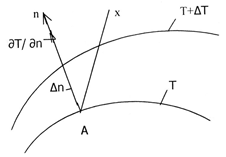
Совокупность значений температуры в данный момент времени для всех точек изучаемого пространства называется температурным полем:

Т= f(x,y,z,т).

Температурное поле, которое изменяется во времени, называется нестационарным (неустановившемся).

В стационарном (установившемся) температурном поле температуры разных точек тела могут быть разными, но не изменяющимися во времени.

Уравнение стационарного температурного поля:

Т= f(x,y,z).

Графически температурное поле изображают посредством изотермических поверхностей, под которыми понимается геометрическое место точек с одинаковой температурой.

Кривые, образующиеся в результате пересечения изотермической поверхности и плоскости, называются изотермами

Градиенты температур

 

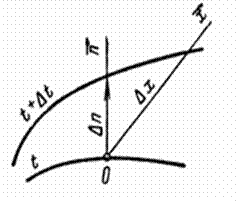
Предел отношения изменения температуры ΔТ к расстоянию между изотермами по нормали Δn, когда Δn стремится к нулю, называют градиентом температуры

| gradt | = lim [∆ t /∆ n ]∆ n →0 = ∂ t /∂ n,

      

   Температурный градиент-это вектор, направленной по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной температуры t по нормали n:

 

gradt = ∂t/∂n,

 

 

Градиент температуры есть вектор, направленный по нормали к изотермической поверхности в сторону увеличения температуры и численно равный частной производной от температуры по этому направлению.

 

За положительное направление градиента принимается направление возрастания

температур, его размерность °С/м

Тепловой поток

Количество теплоты, переносимой за единицу времени через произвольную изотермическую поверхность площадью F, называется тепловым потоком Q.

Единицей измерения которого служит ватт(вт).

 Тепловой поток, отнесённый к единице поверхности,называется плотностью теплового потока, или удельным тепловым потоком,

Единицей измерения q является ватт на квадратный метр (вт/м2).

Связь между Q и q устанавливается из определений: 

 

q = dQ/dF,                       Q = q F.

 

Если тепловой поток отнесен к единице изотермической поверхности, то величина q является вектором, направление которого совпадает с направлением распространения тепла в данной точке и противоположно направлению вектора температурного градиента.

 

ЗАКОН ФУРЬЕ

Основным законом теплопроводности является предложенная Фурье

Гипотеза, подтвержденная опытами, о пропорциональности теплового потока градиенту

Температуры.

   К оличество переданного тепла пропорционально падению температуры, времени и площади сечения, перпендикулярного направлению распространения тепла.

   Математическое выражение закона Фурье для плотности теплового потока имеет вид:
                                          

где λ называют коэффициентом теплопроводности

Плотность теплового потока q – векторная величина. Вектор q направлен в сторону уменьшения температуры. Знак минус в уравнении отражает противоположность направлений векторов плотности теплового потока и температурного градиента.